18.1 平行四边形同步练习(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学四边形章节测试卷
姓名:
分数:
1、
单选题(每题3分;共36分)
1.如图,四边形
是平行四边形,
是
延长线上的一点,若
,则
的度数是(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
2.如图,在
ABCD
中,对角线
AC,BD
相交于点
O,下列结论一定成立的是(??
)
A.?AC=BC???????????????????????B.?AO=OC???????????????????????C.????????????????????????D.?
3.如图,四边形ABCD中,AB∥CD,BC∥AD,点E、F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为(??
)
A.?∠1=∠2????????????????????????????B.?BF=DE????????????????????????????C.?AE=CF????????????????????????????D.?∠AED=∠CFB
4.如图,在
ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于(???
)
A.?35°???????????????????????????????????????B.?30°???????????????????????????????????????C.?25°???????????????????????????????????????D.?20°
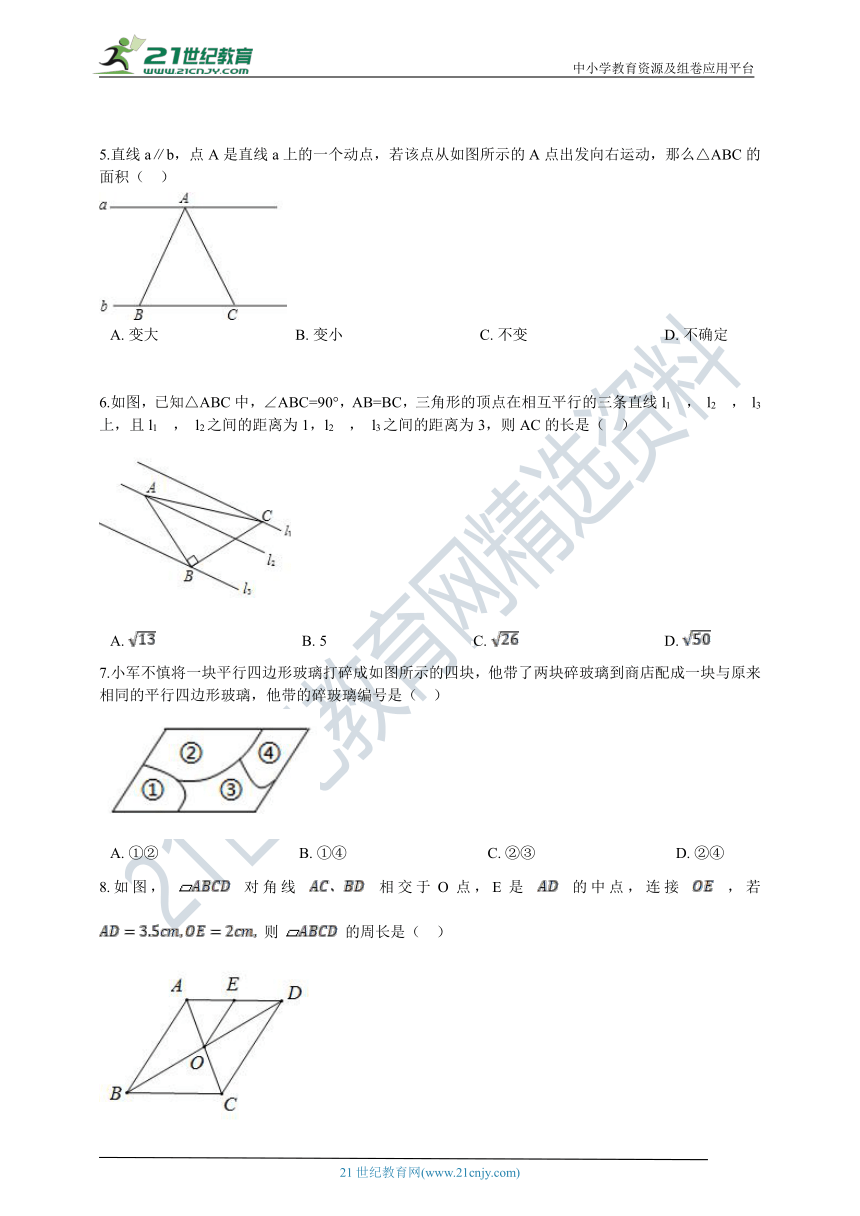
5.直线a∥b,点A是直线a上的一个动点,若该点从如图所示的A点出发向右运动,那么△ABC的面积(??
)
A.?变大????????????????????????????????????B.?变小????????????????????????????????????C.?不变????????????????????????????????????D.?不确定
6.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1
,
l2
,
l3
上,且l1
,
l2之间的距离为1,l2
,
l3之间的距离为3,则AC的长是(??
)
A.???????????????????????????????????????B.?5??????????????????????????????????????C.???????????????????????????????????????D.?
7.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(??
)
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
8.如图,
对角线
相交于O点,E是
的中点,连接
,若
则
的周长是(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
9.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
10.如图,在四边形ABCD中,对角线AC,BD交于点O,下列选项不能得到四边形ABCD是平行四边形的是(???
)
A.?AC=BD,OA=OC?????????B.?OB=OD,OA=OC?????????C.?AD=BC,AD∥BC?????????D.?△ABC≌△CDA
11.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为
、
、
,若
=3,
=8,则
的值为(??
)
A.?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?44?????????????????????????????????????????D.?48
12.如图,
的对角线AC,BD交于点O,AE平分
,交BC于点E,且
,连接OE,下列结论①
;②OD=AB;③
;④
;其中成立的个数是(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(每题3分;共12分)
13.如图,
中,
和
的平分线分别交
于E、F两点,
、
交与点G,若
,
,则
________.
14.如图,在?ABCD中,AB=4,BC=9,∠B=30°,则?ABCD的面积是________.
15.如图,在平行四边形ABCD中,AB=8,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=2,则AE的长为________.
16.在如图所示的方格纸中,每个小方格都是边长为
1
的正方形,
点
A,B
是方格纸中的两个格点(即正方形的顶点),在这个5×5
的方格纸中,找出格点
C
使△ABC
的面积为
2,则满足条件的格点
C
的个数是________个.
三、解答题(共72分)
17(10分).已知:如图,AD=BC且AD∥BC,
E、F是AC上的两点,且AF=CE.
求证:DE=BF且DE∥BF.
18(10分).如图,四边形
ABCD
和四边形
CDEF
均为平行四边形,连接
AE,BF.求证:AE=BF.
19(10分).如图所示,O是平行四边形ABCD对角线的交点,过点O的直线EF分别交AD,
BC于F,E两点,连结AE,CF,求证:四边形AECF是平行四边形.
20(10分).如图,E是?ABCD的边AB的中点,连接CE并延长交DA的延长线于F,若BC=8,求DF的长.
21(10分).如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
22(10分).如图,依次连接四边形
四边的中点
,得到的新四边形
是什么四边形?请证明.
23(12分).如图,在平行四边形ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,连结BF,DE。
(1)求证:四边形BF
DE是平行四边形;
(2)连结BD,若BE=3,BF=5,求BD的长。
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
B
3.【答案】
C
4.【答案】
D
5.【答案】
C
6.【答案】
D
7.【答案】
C
8.【答案】
A
9.【答案】
B
10.【答案】
A
11.【答案】
C
12.【答案】
C
二、填空题
34.【答案】
4
36.【答案】
18
37.【答案】
8
30.【答案】
5
三、解答题
38.【答案】
证明:∵AD=BC且AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS),
∴DE=BF,∠DEF=∠BFA,
∴DE∥BF
39.【答案】
证明:∵四边形
ABCD,CDEF
均为平行四边形,
∴AB
∥
CD,AB=CD,CD
∥
EF,CD=EF,
∴AB
∥
EF,AB=EF,
∴四边形
ABFE
为平行四边形,
∴AE=BF.
44.【答案】
证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠EBO=∠FDO,
∵O是平行四边形ABCD对角线的交点,
∴BO=DO,AO=CO,
在△DFO和△BEO中,有
∠EBO=∠FDO,BO=DO,∠BOE=∠DOF,
∴△DFO≌△BEO(ASA),
∴OF=OE,
∵AO=CO,
∴四边形AECF为平行四边形.
45.【答案】
解:∵E是?ABCD的边AB的中点,
∴AE=BE,
∵四边形ABCD是平行四边形,
∴AD=CB=8,AD∥CB,
∴∠F=∠BCE,
在△AEF和△BEC中,
,
∴△AEF≌△BEC(AAS),
∴AF=CB=8,
∴DF=AD+AF=16.
48.【答案】
解:猜想:BE∥DF,BE=DF.
证明:如图1
∵四边形ABCD是平行四边形,
∴BC=AD,∠1=∠2,
又∵CE=AF,
∴△BCE≌△DAF.
∴BE=DF,∠3=∠4.
∴BE∥DF.
49.【答案】
解:四边形EFGH是平行四边形,理由如下:
连接BD
∵E,H分别是AB,AD的中点
∴EH∥BD,EH=
同理FG∥BD,FG=
∴EH∥FG且EH=FG
∴四边形EFGH是平行四边形
50.【答案】
(1)证明:在平行四边形ABCD中,
AB∥CD,
AB=CD,
∴∠BAE=∠DCF
∵BE⊥AC,DF⊥AC,
∴∠BEA=90°=∠DF
C,
BE∥DF,
∴△ABE≌△CDF,
∴BE=DF,
∴四边形BFDE是平行四边形
(2)解:连结BD交AC于点O,
则OE=OF,OB=OD
∵BE⊥AC,BE=3,BF=5,
∴EF=4,OE=2
在Rt△OBE中,OB=
∴BD=2OB=2
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级数学四边形章节测试卷
姓名:
分数:
1、
单选题(每题3分;共36分)
1.如图,四边形
是平行四边形,
是
延长线上的一点,若
,则
的度数是(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
2.如图,在
ABCD
中,对角线
AC,BD
相交于点
O,下列结论一定成立的是(??
)
A.?AC=BC???????????????????????B.?AO=OC???????????????????????C.????????????????????????D.?
3.如图,四边形ABCD中,AB∥CD,BC∥AD,点E、F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为(??
)
A.?∠1=∠2????????????????????????????B.?BF=DE????????????????????????????C.?AE=CF????????????????????????????D.?∠AED=∠CFB
4.如图,在
ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于(???
)
A.?35°???????????????????????????????????????B.?30°???????????????????????????????????????C.?25°???????????????????????????????????????D.?20°
5.直线a∥b,点A是直线a上的一个动点,若该点从如图所示的A点出发向右运动,那么△ABC的面积(??
)
A.?变大????????????????????????????????????B.?变小????????????????????????????????????C.?不变????????????????????????????????????D.?不确定
6.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1
,
l2
,
l3
上,且l1
,
l2之间的距离为1,l2
,
l3之间的距离为3,则AC的长是(??
)
A.???????????????????????????????????????B.?5??????????????????????????????????????C.???????????????????????????????????????D.?
7.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(??
)
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
8.如图,
对角线
相交于O点,E是
的中点,连接
,若
则
的周长是(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
9.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
10.如图,在四边形ABCD中,对角线AC,BD交于点O,下列选项不能得到四边形ABCD是平行四边形的是(???
)
A.?AC=BD,OA=OC?????????B.?OB=OD,OA=OC?????????C.?AD=BC,AD∥BC?????????D.?△ABC≌△CDA
11.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为
、
、
,若
=3,
=8,则
的值为(??
)
A.?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?44?????????????????????????????????????????D.?48
12.如图,
的对角线AC,BD交于点O,AE平分
,交BC于点E,且
,连接OE,下列结论①
;②OD=AB;③
;④
;其中成立的个数是(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(每题3分;共12分)
13.如图,
中,
和
的平分线分别交
于E、F两点,
、
交与点G,若
,
,则
________.
14.如图,在?ABCD中,AB=4,BC=9,∠B=30°,则?ABCD的面积是________.
15.如图,在平行四边形ABCD中,AB=8,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=2,则AE的长为________.
16.在如图所示的方格纸中,每个小方格都是边长为
1
的正方形,
点
A,B
是方格纸中的两个格点(即正方形的顶点),在这个5×5
的方格纸中,找出格点
C
使△ABC
的面积为
2,则满足条件的格点
C
的个数是________个.
三、解答题(共72分)
17(10分).已知:如图,AD=BC且AD∥BC,
E、F是AC上的两点,且AF=CE.
求证:DE=BF且DE∥BF.
18(10分).如图,四边形
ABCD
和四边形
CDEF
均为平行四边形,连接
AE,BF.求证:AE=BF.
19(10分).如图所示,O是平行四边形ABCD对角线的交点,过点O的直线EF分别交AD,
BC于F,E两点,连结AE,CF,求证:四边形AECF是平行四边形.
20(10分).如图,E是?ABCD的边AB的中点,连接CE并延长交DA的延长线于F,若BC=8,求DF的长.
21(10分).如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
22(10分).如图,依次连接四边形
四边的中点
,得到的新四边形
是什么四边形?请证明.
23(12分).如图,在平行四边形ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,连结BF,DE。
(1)求证:四边形BF
DE是平行四边形;
(2)连结BD,若BE=3,BF=5,求BD的长。
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
B
3.【答案】
C
4.【答案】
D
5.【答案】
C
6.【答案】
D
7.【答案】
C
8.【答案】
A
9.【答案】
B
10.【答案】
A
11.【答案】
C
12.【答案】
C
二、填空题
34.【答案】
4
36.【答案】
18
37.【答案】
8
30.【答案】
5
三、解答题
38.【答案】
证明:∵AD=BC且AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS),
∴DE=BF,∠DEF=∠BFA,
∴DE∥BF
39.【答案】
证明:∵四边形
ABCD,CDEF
均为平行四边形,
∴AB
∥
CD,AB=CD,CD
∥
EF,CD=EF,
∴AB
∥
EF,AB=EF,
∴四边形
ABFE
为平行四边形,
∴AE=BF.
44.【答案】
证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠EBO=∠FDO,
∵O是平行四边形ABCD对角线的交点,
∴BO=DO,AO=CO,
在△DFO和△BEO中,有
∠EBO=∠FDO,BO=DO,∠BOE=∠DOF,
∴△DFO≌△BEO(ASA),
∴OF=OE,
∵AO=CO,
∴四边形AECF为平行四边形.
45.【答案】
解:∵E是?ABCD的边AB的中点,
∴AE=BE,
∵四边形ABCD是平行四边形,
∴AD=CB=8,AD∥CB,
∴∠F=∠BCE,
在△AEF和△BEC中,
,
∴△AEF≌△BEC(AAS),
∴AF=CB=8,
∴DF=AD+AF=16.
48.【答案】
解:猜想:BE∥DF,BE=DF.
证明:如图1
∵四边形ABCD是平行四边形,
∴BC=AD,∠1=∠2,
又∵CE=AF,
∴△BCE≌△DAF.
∴BE=DF,∠3=∠4.
∴BE∥DF.
49.【答案】
解:四边形EFGH是平行四边形,理由如下:
连接BD
∵E,H分别是AB,AD的中点
∴EH∥BD,EH=
同理FG∥BD,FG=
∴EH∥FG且EH=FG
∴四边形EFGH是平行四边形
50.【答案】
(1)证明:在平行四边形ABCD中,
AB∥CD,
AB=CD,
∴∠BAE=∠DCF
∵BE⊥AC,DF⊥AC,
∴∠BEA=90°=∠DF
C,
BE∥DF,
∴△ABE≌△CDF,
∴BE=DF,
∴四边形BFDE是平行四边形
(2)解:连结BD交AC于点O,
则OE=OF,OB=OD
∵BE⊥AC,BE=3,BF=5,
∴EF=4,OE=2
在Rt△OBE中,OB=
∴BD=2OB=2
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
