第一章 静电场 学案 Word版含答案
文档属性
| 名称 | 第一章 静电场 学案 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 640.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览




文档简介
第一章
【典例1】(2019·海南高考)如图,静电场中的一条电场线上有M、N两点,箭头代表电场的方向,则 ( )
A.M点的电势比N点的低
B.M点的场强大小一定比N点的大
C.电子在M点的电势能比在N点的低
D.电子在M点受到的电场力大小一定比在N点的大
【解析】选C。电势沿电场的方向降低,A错误;电子从M点向N移动时克服电场力做功,电势能增大,故电子在M点的电势能比在N点的低,选项C正确;因为一条电场线不能判断M、N两点的电场强度的大小,所以也不能判断电子在M点受到的电场力大小比在N点的大,选项B、D错误。
(2020·德阳高二检测)如图所示,在点电荷Q形成的电场中,已知a、b两点在同一等势面上,c、d两点在另一等势面上。甲、乙两个带电粒子的运动轨迹分别为acb和adb曲线,已知乙粒子带正电。那么下列判断正确的是( )
A.甲粒子在b点的电势能比在c点小
B.乙粒子在d点速度最大
C.a、b两点电场强度相同
D.d点电势比b点电势高
【解析】选D。由题图可知,甲粒子受到中心点电荷Q的引力,甲粒子从c到b的过程中电场力做负功,电势能增大,所以甲粒子在b点的电势能比在c点大,故A错误;乙粒子受到中心点电荷Q的排斥力,从a到d电场力做负功,动能减小,速度减小。从d到b电场力做正功,动能增大,速度增大,所以乙粒子在d点速度最小,故B错误;a、b两点电场强度大小相等,方向不同,则电场强度不同,故C错误。越靠近正点电荷Q电势越高,则d点电势比b点电势高,故D正确。故选D。
【加固训练】
如图所示,正点电荷Q、2Q分别置于M、N两点, O点为MN连线的中点,点a为MO的中点,点b为ON的中点,点c、d在M、N中垂线上,关于O点对称。下列说法正确的是 ( )
A.a、b两点的电场强度相同
B.O点的电势高于c点的电势
C.将电子沿直线从a点移到b点,电场力对电子先做正功后做负功
D.将电子沿直线从c点移到d点,电场力对电子先做负功后做正功
【解析】选B。同种电荷的电场线是排斥状的,沿电场线方向电势逐渐降低,知O点的电势高于c点的电势。故B正确;设Ma=L,aO=r,则a点的电场强度Ea=k-k,Eb=k-k,可见Ea≠Eb,故A错误;电子受到的电场力方向与电场方向相反,所以将电子沿直线从a点移到b点,电场力对电子先做负功后做正功,C错误;对两个电荷在中垂线上的场强进行叠加,在Oc段方向斜向左上,在Od段方向斜向左下,所以电子所受的电场力在Oc段斜向右下,在Od段斜向右上,电场力跟速度的方向先是锐角后是钝角,电场力对电子先做正功后做负功,故D错误。
考 点 静电场中的带电物体
1.处于静电场中的物体:
(1)带电物体在静电场中的平衡。
(2)静电平衡。
(3)电场力做功只与起点和终点的位置有关与电荷移动的路径无关。
(4)电荷在电场中加速和偏转。
2.处理静电场中物体运动问题的一般方法:
情景 运动规律
静电场中物体的平衡
物体所受合力为零
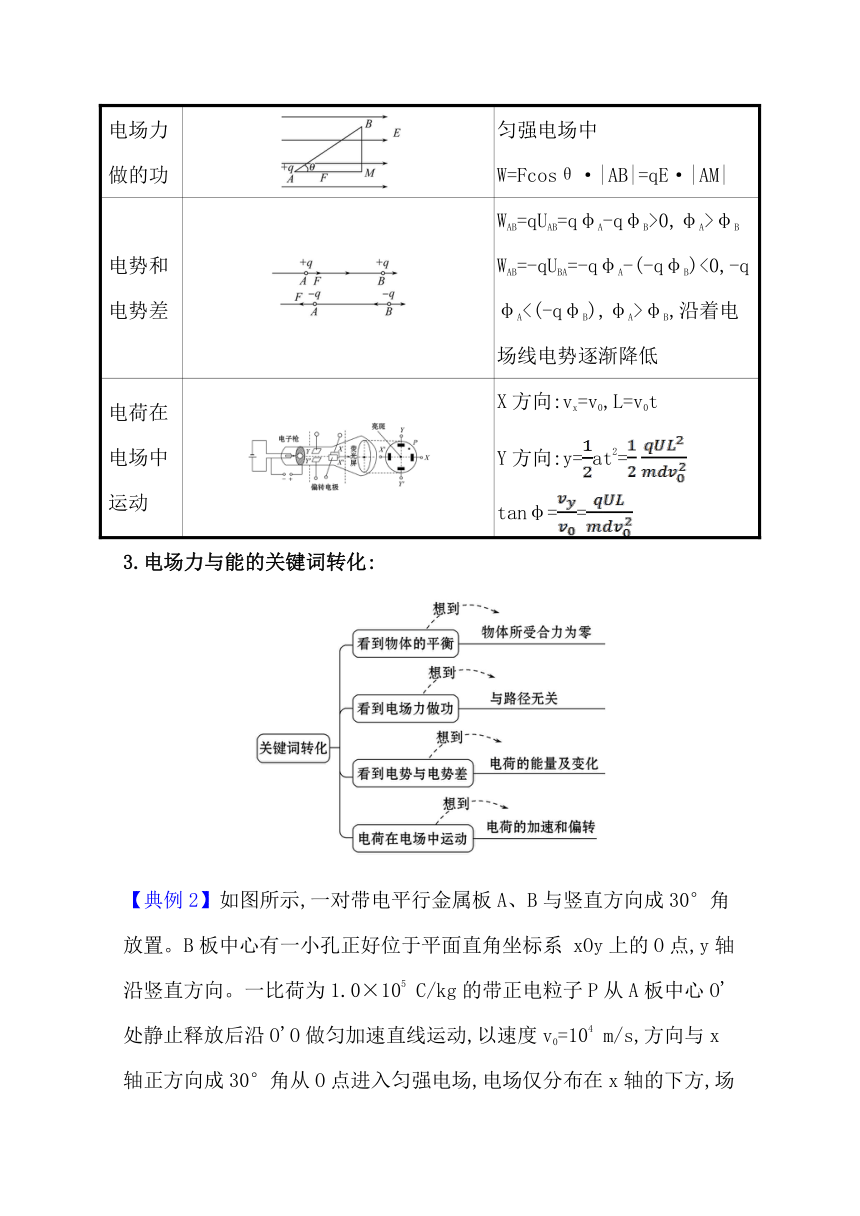
电场力做的功
匀强电场中W=Fcosθ·|AB|=qE·|AM|
电势和电势差
WAB=qUAB=qφA-qφB>0,φA>φB
WAB=-qUBA=-qφA-(-qφB)<0,-qφA<(-qφB),φA>φB,沿着电场线电势逐渐降低
电荷在电场中运动
X方向:vx=v0,L=v0t
Y方向:y=at2=
tanφ==
3.电场力与能的关键词转化:
【典例2】如图所示,一对带电平行金属板A、B与竖直方向成30°角放置。B板中心有一小孔正好位于平面直角坐标系 xOy上的O点,y轴沿竖直方向。一比荷为1.0×105 C/kg的带正电粒子P从A板中心O'处静止释放后沿O'O做匀加速直线运动,以速度v0=104 m/s,方向与x轴正方向成30°角从O点进入匀强电场,电场仅分布在x轴的下方,场强为E=×103 V/m,方向与x轴正方向成60°角斜向上,粒子的重力不计。试求:
(1)AB两板间的电势差UAB。
(2)粒子P离开电场时的坐标。
(3)若在P进入电场的同时,在电场中适当的位置由静止释放另一与P完全相同的带电粒子Q,可使两粒子在离开电场前相遇。求所有满足条件的释放点的范围(不计两粒子之间的相互作用力)。
【解析】(1)由动能定理qUAB=m可得
UAB=== V=500 V
(2)粒子P在进入电场后做类平抛运动,设离开电场时距O距离为L,如图所示,
则Lcos30°=v0t
Lsin30°=t2
解得 L=1 m
所以P离开电场时的坐标为(1 m,0)
(3)由于粒子Q与P完全相同,所以只需在P进入电场时速度方向的直线上的OM范围内任一点释放粒子Q,可保证两者在离开电场前相碰,所在的直线方程为
y=-x
OM=Lcos30°= m
故M的横坐标为xM=OM·cos30°=0.75 m
所以所有满足条件的释放点的范围为y=-x且0≤x≤0.75 m。
答案:(1)500 V (2)(1 m,0)
(3)y=-x且0≤x≤0.75 m
1.(2020·眉山高二检测)一边长为r的正三角形的三个顶点,固定有3个点电荷,电荷量分别为+q、+q和-2q,如图,静电力常量为k,则三角形中心处O点的电场强度大小和方向为 ( )
A.,指向电荷量为-2q的点电荷
B.,指向电荷量为-2q的点电荷
C.,背离电荷量为-2q的点电荷
D.,背离电荷量为-2q的点电荷
【解析】选B。O点是三角形的中心,到三个电荷的距离为l=r×sin60°=r,两个+q电荷在O处产生的场强大小均为E1=E2=k;根据对称性和几何知识得知:两个+q在O处产生的合场强为E12=E1=k;再与-2q在O处产生的场强进行合成,得到O点的合场强为E=E12+E3=k+k=k=,方向指向电荷量为-2q 的点电荷,故选B。
2.(2020·泉州高二检测)如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成,如果在荧光屏上P点出现亮斑那么示波管中的 ( )
①极板X应带正电 ②极板X'应带正电
③极板Y应带正电 ④极板Y'应带正电
A.①③ B.①④ C.②③ D.②④
【解析】选A。电子受力方向与电场方向相反,因电子向X方向偏转,则电场方向为X到X',则X带正电;同理可知Y带正电,故①③正确,②④错误,故选A。
考 点 电容器
1.电容器:
物理观念 物理过程 物理规律
电容器 充电和放电 两极板带等量异号的电荷,电容器的带电量就是一个极板所带电量的绝对值
电容 C= C=
电容器内的电场 两极板之间是匀强电场 E=
电荷在电容器内的运动 加速和偏转 qU1=mv2
L=v0t
y=at2= tanφ
==
2.电容器问题的关键词转化:
【典例3】如图甲所示,A、B为两块靠得很近的平行金属板,板中央均有小孔。一束电子以初动能Ek= 120 eV,从A板上的小孔O不断垂直于板射入A、B之间,在B板右侧,平行金属板的板长L= 2×10-2 m,板间距离d= 4×10-3 m,两板上所加电压为U2 = 20 V。现在在A、B两板上加一个如图乙所示的变化电压U1,在t=0到t=2 s时间内,A板电势高于B板,则在U1随时间变化的第一个周期内:
(1)电子在哪段时间内可以从B板小孔射出?
(2)在哪段时间内,电子能从偏转电场右侧飞出?(由于A、B两板距离很近,可以认为电子穿过A、B板间所用时间很短,可以不计电压变化)
【解析】(1) 能射出B板,要求电子到达B板时速度大于或等于零,
由动能定理得- eU1 = 0-,
又Ek = ,所以U1 = 120 V;
AB两板所加电压在0~1 s区间里有U1=200t,故U1=200t1,得t1=0.6 s。由电压图像的对称性,另一对应时刻t2=1.4 s。在下半周期,电场力做正功电子均能射出,
所以能射出的时间段为0~0.6 s及1.4~4 s。
(2)设电子从偏转电场中垂直射入时速度为v0,那么侧移量
y=()()2=,y≤才能射出,
所以≤,Ek'≥250 eV。
又Ek'=eU1+Ek=eU1+120 eV,
所以120 eV+eU1≥250 eV,U1≥130 V;
又因t1=(+2)s=2.65 s、t2=(4-)s=3.35 s,所以在2.65~3.35 s内有电子从偏转电场右侧飞出。
答案:见解析
1.(2020·绵阳高二检测)如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫作偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是 ( )
A.增大U1 B.增大U2
C.减小L D.增大d
【解析】选B。电子在加速电场中加速,根据动能定理可得,eU1=m,所以电子进入偏转电场时速度的大小为v0=,电子进入偏转电场后的偏转位移为y=at2=·()2=,所以为了增大偏转距离,可以增大L、减小d、减小U1、增大U2,故B正确,A、C、D错误;故选B。
2.一平行板电容器充电后与电源断开,负极板接地。两板间有一个正试探电荷固定在P点,如图所示,以C表示电容器的电容、E表示两板间的场强、φ表示P点的电势,Ep表示正电荷在P点的电势能。若正极板保持不动,将负极板缓慢向右平移一小段距离l0(移动过程可认为平行板电容器的电量保持不变),那么在此过程中,各物理量与负极板移动距离x的关系图像中正确的是 ( )
【解析】选C。当负极板右移时,d减小,由C=可知,C与d成反比,故A错误;由U=,E=可知,E=,故E与d无关,故B错误;因负极板接地,设P点原来距负极板为l,则P点的电势φ=E(l-x),故C正确;电势能Ep=φq=Eq(l-x),不可能为水平线,故D错误;故选C。
3.如图所示为一真空示波管的示意图,电子从灯丝K发出(初速度可忽略不计),经灯丝与A板间的电压U1加速,从A板中心孔沿中心线KO射出,然后进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),电子进入M、N间电场时的速度与电场方向垂直,电子经过偏转电场后打在荧光屏上的P点。已知M、N两板间的电压为U2,两板间的距离为d,板长为L,电子的质量为m,电荷量为e,不计电子受到的重力及它们之间的相互作用力。
(1)求电子穿过A板时速度的大小;
(2)求电子从偏转电场射出时的侧移量;
(3)若要使电子打在荧光屏上P点的上方,可采取哪些措施?
【解析】(1)设电子经电压U1加速后的速度为v0,由动能定理得
eU1=m-0
解得:v0=。
(2)电子以速度v0进入偏转电场后,做类平抛运动,设电子离开偏转电场时的侧移量为y
沿初速度方向做匀速直线运动,有 L=v0t
垂直初速度方向,有y=at2,
又因为电场力F=eE=e,
根据F=ma,得加速度为:a=,
解得:y=。
(3)要使电子打在P点上方,需增大侧移量,由解得
y=知,可以减小加速电压U1或增大偏转电压U2。
答案:(1)
(2)
(3)见解析
【典例1】(2019·海南高考)如图,静电场中的一条电场线上有M、N两点,箭头代表电场的方向,则 ( )
A.M点的电势比N点的低
B.M点的场强大小一定比N点的大
C.电子在M点的电势能比在N点的低
D.电子在M点受到的电场力大小一定比在N点的大
【解析】选C。电势沿电场的方向降低,A错误;电子从M点向N移动时克服电场力做功,电势能增大,故电子在M点的电势能比在N点的低,选项C正确;因为一条电场线不能判断M、N两点的电场强度的大小,所以也不能判断电子在M点受到的电场力大小比在N点的大,选项B、D错误。
(2020·德阳高二检测)如图所示,在点电荷Q形成的电场中,已知a、b两点在同一等势面上,c、d两点在另一等势面上。甲、乙两个带电粒子的运动轨迹分别为acb和adb曲线,已知乙粒子带正电。那么下列判断正确的是( )
A.甲粒子在b点的电势能比在c点小
B.乙粒子在d点速度最大
C.a、b两点电场强度相同
D.d点电势比b点电势高
【解析】选D。由题图可知,甲粒子受到中心点电荷Q的引力,甲粒子从c到b的过程中电场力做负功,电势能增大,所以甲粒子在b点的电势能比在c点大,故A错误;乙粒子受到中心点电荷Q的排斥力,从a到d电场力做负功,动能减小,速度减小。从d到b电场力做正功,动能增大,速度增大,所以乙粒子在d点速度最小,故B错误;a、b两点电场强度大小相等,方向不同,则电场强度不同,故C错误。越靠近正点电荷Q电势越高,则d点电势比b点电势高,故D正确。故选D。
【加固训练】
如图所示,正点电荷Q、2Q分别置于M、N两点, O点为MN连线的中点,点a为MO的中点,点b为ON的中点,点c、d在M、N中垂线上,关于O点对称。下列说法正确的是 ( )
A.a、b两点的电场强度相同
B.O点的电势高于c点的电势
C.将电子沿直线从a点移到b点,电场力对电子先做正功后做负功
D.将电子沿直线从c点移到d点,电场力对电子先做负功后做正功
【解析】选B。同种电荷的电场线是排斥状的,沿电场线方向电势逐渐降低,知O点的电势高于c点的电势。故B正确;设Ma=L,aO=r,则a点的电场强度Ea=k-k,Eb=k-k,可见Ea≠Eb,故A错误;电子受到的电场力方向与电场方向相反,所以将电子沿直线从a点移到b点,电场力对电子先做负功后做正功,C错误;对两个电荷在中垂线上的场强进行叠加,在Oc段方向斜向左上,在Od段方向斜向左下,所以电子所受的电场力在Oc段斜向右下,在Od段斜向右上,电场力跟速度的方向先是锐角后是钝角,电场力对电子先做正功后做负功,故D错误。
考 点 静电场中的带电物体
1.处于静电场中的物体:
(1)带电物体在静电场中的平衡。
(2)静电平衡。
(3)电场力做功只与起点和终点的位置有关与电荷移动的路径无关。
(4)电荷在电场中加速和偏转。
2.处理静电场中物体运动问题的一般方法:
情景 运动规律
静电场中物体的平衡
物体所受合力为零
电场力做的功
匀强电场中W=Fcosθ·|AB|=qE·|AM|
电势和电势差
WAB=qUAB=qφA-qφB>0,φA>φB
WAB=-qUBA=-qφA-(-qφB)<0,-qφA<(-qφB),φA>φB,沿着电场线电势逐渐降低
电荷在电场中运动
X方向:vx=v0,L=v0t
Y方向:y=at2=
tanφ==
3.电场力与能的关键词转化:
【典例2】如图所示,一对带电平行金属板A、B与竖直方向成30°角放置。B板中心有一小孔正好位于平面直角坐标系 xOy上的O点,y轴沿竖直方向。一比荷为1.0×105 C/kg的带正电粒子P从A板中心O'处静止释放后沿O'O做匀加速直线运动,以速度v0=104 m/s,方向与x轴正方向成30°角从O点进入匀强电场,电场仅分布在x轴的下方,场强为E=×103 V/m,方向与x轴正方向成60°角斜向上,粒子的重力不计。试求:
(1)AB两板间的电势差UAB。
(2)粒子P离开电场时的坐标。
(3)若在P进入电场的同时,在电场中适当的位置由静止释放另一与P完全相同的带电粒子Q,可使两粒子在离开电场前相遇。求所有满足条件的释放点的范围(不计两粒子之间的相互作用力)。
【解析】(1)由动能定理qUAB=m可得
UAB=== V=500 V
(2)粒子P在进入电场后做类平抛运动,设离开电场时距O距离为L,如图所示,
则Lcos30°=v0t
Lsin30°=t2
解得 L=1 m
所以P离开电场时的坐标为(1 m,0)
(3)由于粒子Q与P完全相同,所以只需在P进入电场时速度方向的直线上的OM范围内任一点释放粒子Q,可保证两者在离开电场前相碰,所在的直线方程为
y=-x
OM=Lcos30°= m
故M的横坐标为xM=OM·cos30°=0.75 m
所以所有满足条件的释放点的范围为y=-x且0≤x≤0.75 m。
答案:(1)500 V (2)(1 m,0)
(3)y=-x且0≤x≤0.75 m
1.(2020·眉山高二检测)一边长为r的正三角形的三个顶点,固定有3个点电荷,电荷量分别为+q、+q和-2q,如图,静电力常量为k,则三角形中心处O点的电场强度大小和方向为 ( )
A.,指向电荷量为-2q的点电荷
B.,指向电荷量为-2q的点电荷
C.,背离电荷量为-2q的点电荷
D.,背离电荷量为-2q的点电荷
【解析】选B。O点是三角形的中心,到三个电荷的距离为l=r×sin60°=r,两个+q电荷在O处产生的场强大小均为E1=E2=k;根据对称性和几何知识得知:两个+q在O处产生的合场强为E12=E1=k;再与-2q在O处产生的场强进行合成,得到O点的合场强为E=E12+E3=k+k=k=,方向指向电荷量为-2q 的点电荷,故选B。
2.(2020·泉州高二检测)如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成,如果在荧光屏上P点出现亮斑那么示波管中的 ( )
①极板X应带正电 ②极板X'应带正电
③极板Y应带正电 ④极板Y'应带正电
A.①③ B.①④ C.②③ D.②④
【解析】选A。电子受力方向与电场方向相反,因电子向X方向偏转,则电场方向为X到X',则X带正电;同理可知Y带正电,故①③正确,②④错误,故选A。
考 点 电容器
1.电容器:
物理观念 物理过程 物理规律
电容器 充电和放电 两极板带等量异号的电荷,电容器的带电量就是一个极板所带电量的绝对值
电容 C= C=
电容器内的电场 两极板之间是匀强电场 E=
电荷在电容器内的运动 加速和偏转 qU1=mv2
L=v0t
y=at2= tanφ
==
2.电容器问题的关键词转化:
【典例3】如图甲所示,A、B为两块靠得很近的平行金属板,板中央均有小孔。一束电子以初动能Ek= 120 eV,从A板上的小孔O不断垂直于板射入A、B之间,在B板右侧,平行金属板的板长L= 2×10-2 m,板间距离d= 4×10-3 m,两板上所加电压为U2 = 20 V。现在在A、B两板上加一个如图乙所示的变化电压U1,在t=0到t=2 s时间内,A板电势高于B板,则在U1随时间变化的第一个周期内:
(1)电子在哪段时间内可以从B板小孔射出?
(2)在哪段时间内,电子能从偏转电场右侧飞出?(由于A、B两板距离很近,可以认为电子穿过A、B板间所用时间很短,可以不计电压变化)
【解析】(1) 能射出B板,要求电子到达B板时速度大于或等于零,
由动能定理得- eU1 = 0-,
又Ek = ,所以U1 = 120 V;
AB两板所加电压在0~1 s区间里有U1=200t,故U1=200t1,得t1=0.6 s。由电压图像的对称性,另一对应时刻t2=1.4 s。在下半周期,电场力做正功电子均能射出,
所以能射出的时间段为0~0.6 s及1.4~4 s。
(2)设电子从偏转电场中垂直射入时速度为v0,那么侧移量
y=()()2=,y≤才能射出,
所以≤,Ek'≥250 eV。
又Ek'=eU1+Ek=eU1+120 eV,
所以120 eV+eU1≥250 eV,U1≥130 V;
又因t1=(+2)s=2.65 s、t2=(4-)s=3.35 s,所以在2.65~3.35 s内有电子从偏转电场右侧飞出。
答案:见解析
1.(2020·绵阳高二检测)如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫作偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是 ( )
A.增大U1 B.增大U2
C.减小L D.增大d
【解析】选B。电子在加速电场中加速,根据动能定理可得,eU1=m,所以电子进入偏转电场时速度的大小为v0=,电子进入偏转电场后的偏转位移为y=at2=·()2=,所以为了增大偏转距离,可以增大L、减小d、减小U1、增大U2,故B正确,A、C、D错误;故选B。
2.一平行板电容器充电后与电源断开,负极板接地。两板间有一个正试探电荷固定在P点,如图所示,以C表示电容器的电容、E表示两板间的场强、φ表示P点的电势,Ep表示正电荷在P点的电势能。若正极板保持不动,将负极板缓慢向右平移一小段距离l0(移动过程可认为平行板电容器的电量保持不变),那么在此过程中,各物理量与负极板移动距离x的关系图像中正确的是 ( )
【解析】选C。当负极板右移时,d减小,由C=可知,C与d成反比,故A错误;由U=,E=可知,E=,故E与d无关,故B错误;因负极板接地,设P点原来距负极板为l,则P点的电势φ=E(l-x),故C正确;电势能Ep=φq=Eq(l-x),不可能为水平线,故D错误;故选C。
3.如图所示为一真空示波管的示意图,电子从灯丝K发出(初速度可忽略不计),经灯丝与A板间的电压U1加速,从A板中心孔沿中心线KO射出,然后进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),电子进入M、N间电场时的速度与电场方向垂直,电子经过偏转电场后打在荧光屏上的P点。已知M、N两板间的电压为U2,两板间的距离为d,板长为L,电子的质量为m,电荷量为e,不计电子受到的重力及它们之间的相互作用力。
(1)求电子穿过A板时速度的大小;
(2)求电子从偏转电场射出时的侧移量;
(3)若要使电子打在荧光屏上P点的上方,可采取哪些措施?
【解析】(1)设电子经电压U1加速后的速度为v0,由动能定理得
eU1=m-0
解得:v0=。
(2)电子以速度v0进入偏转电场后,做类平抛运动,设电子离开偏转电场时的侧移量为y
沿初速度方向做匀速直线运动,有 L=v0t
垂直初速度方向,有y=at2,
又因为电场力F=eE=e,
根据F=ma,得加速度为:a=,
解得:y=。
(3)要使电子打在P点上方,需增大侧移量,由解得
y=知,可以减小加速电压U1或增大偏转电压U2。
答案:(1)
(2)
(3)见解析
同课章节目录
