7.1.2平面直角坐标系课件(共36张)
文档属性
| 名称 | 7.1.2平面直角坐标系课件(共36张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 13:46:25 | ||
图片预览





文档简介
7.1
平面直角坐标系
第七章
平面直角坐标系
7.1.2
平面直角坐标系
学习目标
1.认识并能画出平面直角坐标系,知道点的坐标及象限的含义.
2.能在给定的直角坐标系中,由点的位置写出它的坐标和由点的坐标指出它的位置.
3.经历画坐标系,由点找坐标等过程,发展数形结合意识.
如何确定直线上点的位置?
在直线上规定了原点、正方向、单位长度
就构成了数轴。
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
·
单位长度
0
1
2
3
4
-3
-2
-1
原点
?
?
A
B
导入新课
①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线.所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面.
数学小故事
思考1
如图,数轴上的点A、B表示的数是什么?
表示数字4的点是哪个点?
讲授新课
平面直角坐标系
一
我们曾经利用数轴上的实数来表示直线上的点.
思考:
类似地,能否找到一种方法来表示平面内点的位置呢?
A
B
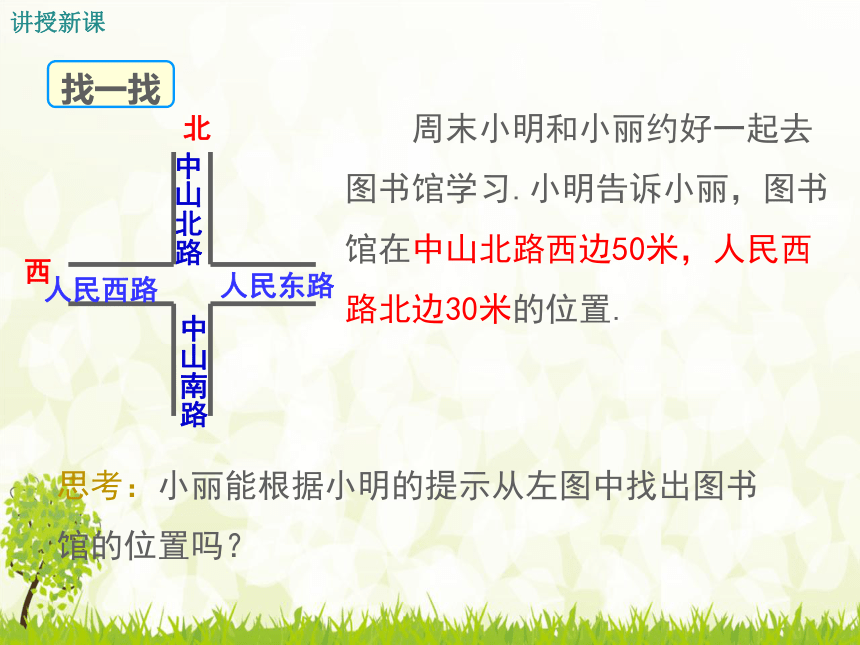
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
讲授新课
中山南路
人民东路
中山北路
人民西路
北
西
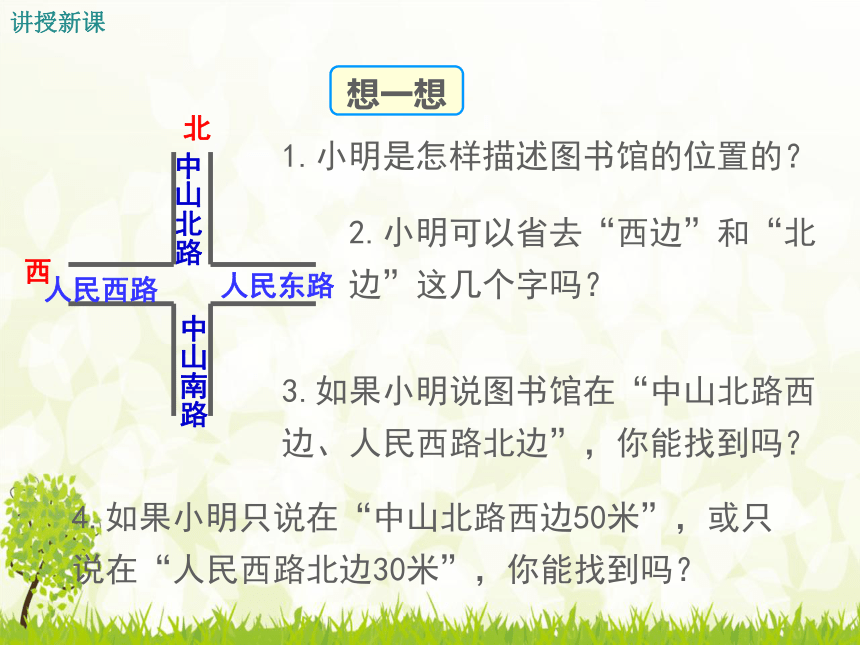
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
讲授新课
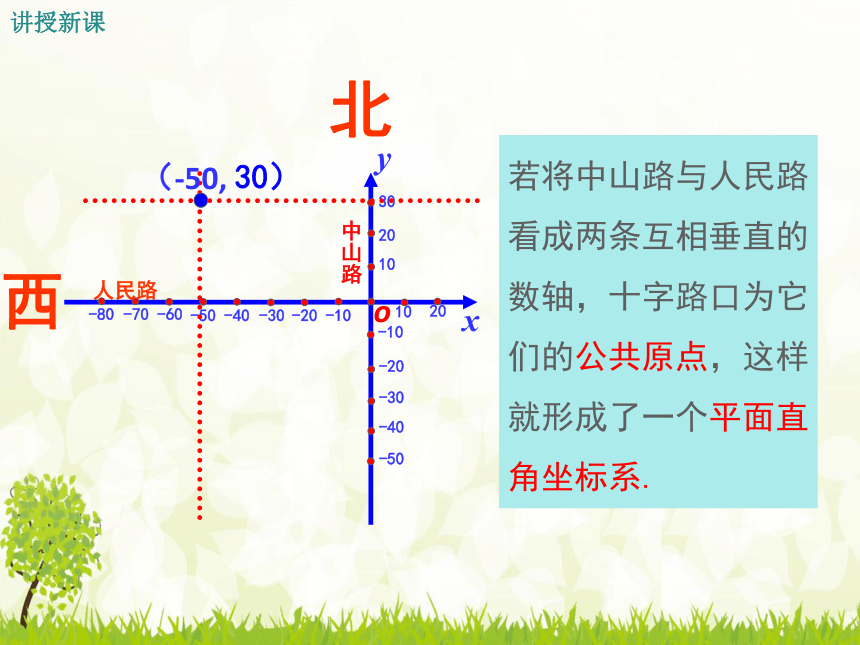
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
讲授新课
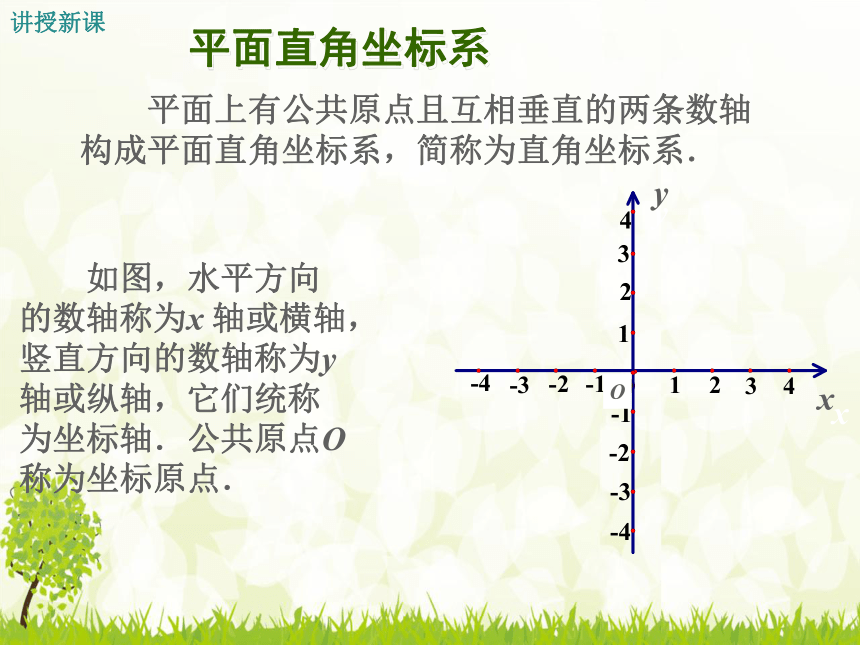
平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系,简称为直角坐标系.
如图,水平方向的数轴称为x
轴或横轴,竖直方向的数轴称为y
轴或纵轴,它们统称为坐标轴.公共原点O称为坐标原点.
平面直角坐标系
x
y
x
y
O
x
y
讲授新课
x
y
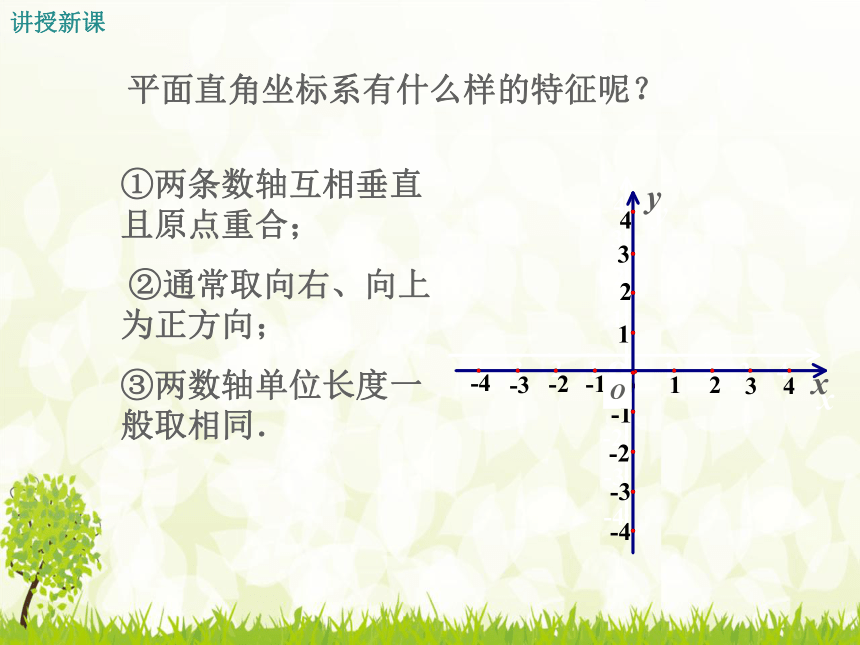
平面直角坐标系有什么样的特征呢?
①两条数轴互相垂直且原点重合;
②通常取向右、向上为正方向;
③两数轴单位长度一般取相同.
x
y
O
讲授新课
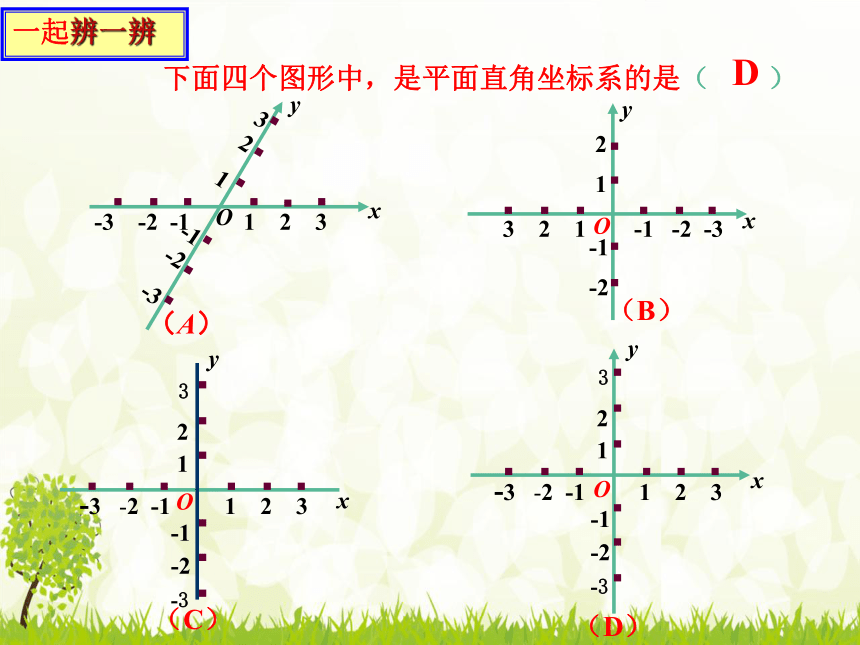
下面四个图形中,是平面直角坐标系的是(
)
2
1
-1
-2
x
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3
2
1
-1
-2
-3
x
y
(B)
O
(C)
O
y
(D)
O
D
3
2
1
-1
-2
-3
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
-3
-2
-1
1
2
3
一起辨一辨
.
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
-1
-2
-3
-4
A
.
B
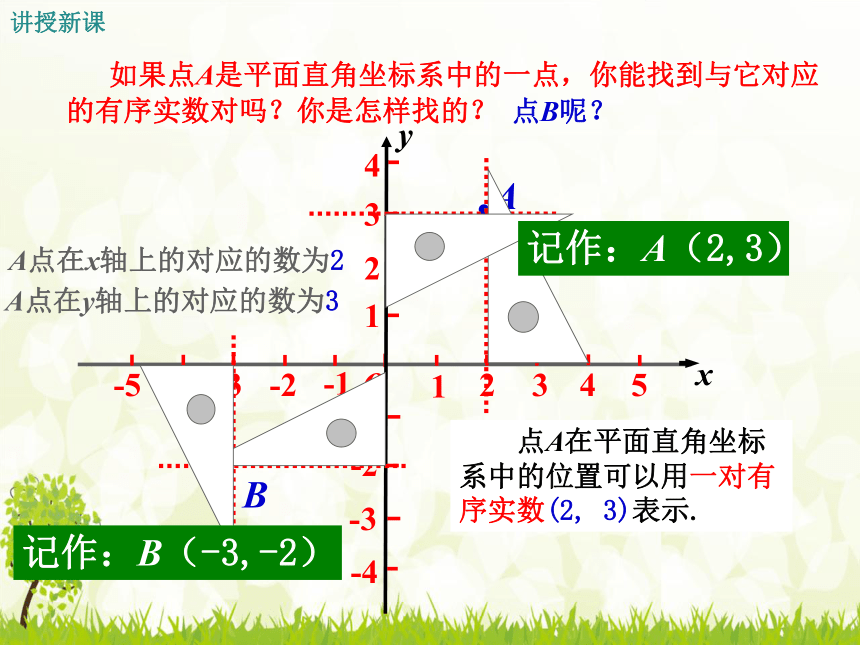
A点在x轴上的对应的数为2
A点在y轴上的对应的数为3
点A在平面直角坐标系中的位置可以用一对有序实数(2,
3)表示.
记作:A(2,3)
记作:B(-3,-2)
如果点A是平面直角坐标系中的一点,你能找到与它对应的有序实数对吗?你是怎样找的?
点B呢?
y
x
讲授新课
在平面直角坐标系中,一对有序实数可以确
定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示.这样的有序实数对叫做点的坐标.
点的坐标通常与表示该点的大写字母写在一起,如
P(a,b),Q(m,n).
讲授新课
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
实数对。
写出图中A、B、C、D、E各点的坐标。
讲授新课
注意:
1.点的坐标通常与表示该点的大写字母写在一起,如
P(a,b).
2.点的坐标的书写方法:
先横后纵,逗号隔开,加上括号.
a称为点P的横坐标
b称为点P的纵坐标
讲授新课
·
A
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x轴上的坐标为4
A点在y轴上的坐标为2
A点在平面直角坐标系中的坐标为
(4,
2)记作:A(4,2)
x轴上的坐标
写在前面
·
B
B(-4,1)
讲授新课
写出如图所示的六边形ABCDEF各个顶点的坐标.
【答案】A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
典例精析
例1:写出下图中的多边形ABCDEF各个顶点的坐标.
在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
练一练
第一象限
第二象限
第三象限
第四象限
仔细观察平面直角坐标系的两条坐标轴将整个平面分成几部分?
注意:
坐标轴上的点不属于任何象限.
x
y
x
y
O
x
y
讲授新课
直角坐标系中点的坐标的特征
二
x
y
(+,+)
(-,+)
(-,-)
(+,-)
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
(-3,3)
(2,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
活动1:
观察坐标系,填写各象限内的点的坐标的特征:
讲授新课
交流:不看平面直角坐标系,你能迅速说出A(4,5)
,
B(-2,3),
C(-4,
-1),
D(2.5,-2),
E(0,-4)所在的象限吗?你的方法又是什么?
讲授新课
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
在x轴上的点,纵坐标等于0;
在y轴上的点,横坐标等于0;
活动2:
观察坐标系,填写坐标轴上的点的坐标的特征:
讲授新课
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
讲授新课
活动3:坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)
(即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
讲授新课
·
B
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
写出图中A,B,C,
D,E的坐标.
例2:请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
讲授新课
思考:满足下列条件的点P(a,b)具有什么特征?
(1)当点P分别落在第一象限、第二象限、
第三象限、第四象限时
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
·
P
·
P
·
P
·
P
(+,+)
(-,+)
(-,-)
(+,-)
x
y
讲授新课
例3
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或者y轴负半轴上(a=0,b<0).
讲授新课
例4
点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2)
B.(2,0)
C.(4,0)
D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
讲授新课
点P(x,y)到x轴的距离为
,
到y轴的距离为
。
注:因为距离是非负数,所以要加绝对值符号。
点到坐标轴的距离:
讲授新课
练一练
已知点P到x轴的距离为3,到y轴的距离为1.如果过点P作两坐标轴的垂线,垂足分别在x轴的正半轴上和y轴的负半轴上,那么点P的坐标是( )
A.(3,-1)
B.(1,-3)
C.(-3,-1)
D.(1,3)
B
抓象限,抓住到x距离看纵坐标,到y的距离看横坐标
本题的易错点有三处:
①混淆距离与坐标之间的区别;
②不知道“点P到x轴的距离”对应的是纵坐标,“点P到y轴的距离”对应的是横坐标;
③忽略坐标的符号出现错解.若本例题只已知距离而无附加条件,则点P的坐标有四个.
方法总结
1.下列点中位于第四象限的是(
)
A.(2,-3)B.(-2,-3)
C.(2,3)D.(-2,3)
2.如xy>0,且x+y<0,那么P(x,y)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.如点P(a,2)在第二象限,那么点Q(-3,a)
在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
C
B
A
当堂练习
4.M(-1,0)、N(0,-1)、P(-2,-1)、Q(5,0)、R(0,-5)、S(-3,2),其中在x轴上
的点的个数是(
)
A.1
B.2
C.3
D.4
当堂练习
5.如图,点A的坐标为
,
点B的坐标为
.
6.在
y轴上的点的横坐标是______,
在
x轴上的点的纵坐标是
______.
7.点
M(-
8,12)到
x轴的距离是_______,
到
y轴的距离是
_________
.
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
当堂练习
8、已知
P
点坐标为(2
a
+
1,a-3)
(
1
)
点
P
在
x
轴上,则
a=
;
(
2
)
点
P
在
y
轴上,则
a=
;
课堂小结
1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标找出点,由点求出坐标。坐标平面内的点和有序实数对是一一对应的。
3、掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.掌握坐标到两坐标轴的距离
68-69页练习1.2题,复习巩固1.2题
课后作业
平面直角坐标系
第七章
平面直角坐标系
7.1.2
平面直角坐标系
学习目标
1.认识并能画出平面直角坐标系,知道点的坐标及象限的含义.
2.能在给定的直角坐标系中,由点的位置写出它的坐标和由点的坐标指出它的位置.
3.经历画坐标系,由点找坐标等过程,发展数形结合意识.
如何确定直线上点的位置?
在直线上规定了原点、正方向、单位长度
就构成了数轴。
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
·
单位长度
0
1
2
3
4
-3
-2
-1
原点
?
?
A
B
导入新课
①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线.所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面.
数学小故事
思考1
如图,数轴上的点A、B表示的数是什么?
表示数字4的点是哪个点?
讲授新课
平面直角坐标系
一
我们曾经利用数轴上的实数来表示直线上的点.
思考:
类似地,能否找到一种方法来表示平面内点的位置呢?
A
B
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
讲授新课
中山南路
人民东路
中山北路
人民西路
北
西
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
讲授新课
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
讲授新课
平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系,简称为直角坐标系.
如图,水平方向的数轴称为x
轴或横轴,竖直方向的数轴称为y
轴或纵轴,它们统称为坐标轴.公共原点O称为坐标原点.
平面直角坐标系
x
y
x
y
O
x
y
讲授新课
x
y
平面直角坐标系有什么样的特征呢?
①两条数轴互相垂直且原点重合;
②通常取向右、向上为正方向;
③两数轴单位长度一般取相同.
x
y
O
讲授新课
下面四个图形中,是平面直角坐标系的是(
)
2
1
-1
-2
x
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3
2
1
-1
-2
-3
x
y
(B)
O
(C)
O
y
(D)
O
D
3
2
1
-1
-2
-3
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
-3
-2
-1
1
2
3
一起辨一辨
.
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
-1
-2
-3
-4
A
.
B
A点在x轴上的对应的数为2
A点在y轴上的对应的数为3
点A在平面直角坐标系中的位置可以用一对有序实数(2,
3)表示.
记作:A(2,3)
记作:B(-3,-2)
如果点A是平面直角坐标系中的一点,你能找到与它对应的有序实数对吗?你是怎样找的?
点B呢?
y
x
讲授新课
在平面直角坐标系中,一对有序实数可以确
定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示.这样的有序实数对叫做点的坐标.
点的坐标通常与表示该点的大写字母写在一起,如
P(a,b),Q(m,n).
讲授新课
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
实数对。
写出图中A、B、C、D、E各点的坐标。
讲授新课
注意:
1.点的坐标通常与表示该点的大写字母写在一起,如
P(a,b).
2.点的坐标的书写方法:
先横后纵,逗号隔开,加上括号.
a称为点P的横坐标
b称为点P的纵坐标
讲授新课
·
A
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x轴上的坐标为4
A点在y轴上的坐标为2
A点在平面直角坐标系中的坐标为
(4,
2)记作:A(4,2)
x轴上的坐标
写在前面
·
B
B(-4,1)
讲授新课
写出如图所示的六边形ABCDEF各个顶点的坐标.
【答案】A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
典例精析
例1:写出下图中的多边形ABCDEF各个顶点的坐标.
在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
练一练
第一象限
第二象限
第三象限
第四象限
仔细观察平面直角坐标系的两条坐标轴将整个平面分成几部分?
注意:
坐标轴上的点不属于任何象限.
x
y
x
y
O
x
y
讲授新课
直角坐标系中点的坐标的特征
二
x
y
(+,+)
(-,+)
(-,-)
(+,-)
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
(-3,3)
(2,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
活动1:
观察坐标系,填写各象限内的点的坐标的特征:
讲授新课
交流:不看平面直角坐标系,你能迅速说出A(4,5)
,
B(-2,3),
C(-4,
-1),
D(2.5,-2),
E(0,-4)所在的象限吗?你的方法又是什么?
讲授新课
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
在x轴上的点,纵坐标等于0;
在y轴上的点,横坐标等于0;
活动2:
观察坐标系,填写坐标轴上的点的坐标的特征:
讲授新课
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
讲授新课
活动3:坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)
(即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
讲授新课
·
B
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
写出图中A,B,C,
D,E的坐标.
例2:请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
讲授新课
思考:满足下列条件的点P(a,b)具有什么特征?
(1)当点P分别落在第一象限、第二象限、
第三象限、第四象限时
3
1
2
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
·
P
·
P
·
P
·
P
(+,+)
(-,+)
(-,-)
(+,-)
x
y
讲授新课
例3
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或者y轴负半轴上(a=0,b<0).
讲授新课
例4
点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2)
B.(2,0)
C.(4,0)
D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
讲授新课
点P(x,y)到x轴的距离为
,
到y轴的距离为
。
注:因为距离是非负数,所以要加绝对值符号。
点到坐标轴的距离:
讲授新课
练一练
已知点P到x轴的距离为3,到y轴的距离为1.如果过点P作两坐标轴的垂线,垂足分别在x轴的正半轴上和y轴的负半轴上,那么点P的坐标是( )
A.(3,-1)
B.(1,-3)
C.(-3,-1)
D.(1,3)
B
抓象限,抓住到x距离看纵坐标,到y的距离看横坐标
本题的易错点有三处:
①混淆距离与坐标之间的区别;
②不知道“点P到x轴的距离”对应的是纵坐标,“点P到y轴的距离”对应的是横坐标;
③忽略坐标的符号出现错解.若本例题只已知距离而无附加条件,则点P的坐标有四个.
方法总结
1.下列点中位于第四象限的是(
)
A.(2,-3)B.(-2,-3)
C.(2,3)D.(-2,3)
2.如xy>0,且x+y<0,那么P(x,y)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.如点P(a,2)在第二象限,那么点Q(-3,a)
在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
C
B
A
当堂练习
4.M(-1,0)、N(0,-1)、P(-2,-1)、Q(5,0)、R(0,-5)、S(-3,2),其中在x轴上
的点的个数是(
)
A.1
B.2
C.3
D.4
当堂练习
5.如图,点A的坐标为
,
点B的坐标为
.
6.在
y轴上的点的横坐标是______,
在
x轴上的点的纵坐标是
______.
7.点
M(-
8,12)到
x轴的距离是_______,
到
y轴的距离是
_________
.
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
当堂练习
8、已知
P
点坐标为(2
a
+
1,a-3)
(
1
)
点
P
在
x
轴上,则
a=
;
(
2
)
点
P
在
y
轴上,则
a=
;
课堂小结
1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标找出点,由点求出坐标。坐标平面内的点和有序实数对是一一对应的。
3、掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.掌握坐标到两坐标轴的距离
68-69页练习1.2题,复习巩固1.2题
课后作业
