2020-2021学年湘教版数学八年级下册 第2章 四边形 单元检测题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年湘教版数学八年级下册 第2章 四边形 单元检测题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 497.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览




文档简介
第2章 四边形
(满分120分)
一、选择题(每小题3分,共30分)
1.平行四边形的对角线一定具有的性质是(
)
A.相等
B.互相平分
C.互相垂直
D.互相垂直且相等
2.下列手机软件图标中,既是轴对称图形又是中心对称图形的是(
)
3.一个多边形的内角和是360°,这个多边形是(
)
A.三角形
B.四边形
C.六边形
D.不能确定
4.如果三角形的两边分别为3和5,那么连接这个三角形三边中点所得三角形的周长可能是(
)
A.5.5
B.5
C.4.5
D.4
5.下列命题中正确的是(
)
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
6.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是(
)
A.1
B.
C.2
D.2
7.如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为(
)
A.
B.
C.5
D.
8.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为(
)
A.1
B.
C.2
D.
9.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图①,测得AC=2;当∠B=60°时,如图②,AC=(
)
A.
B.2
C.
D.2
10.一菱形的周长是20cm,两条对角线的比是4∶3,则菱形的面积是(
)
A.12cm2
B.24cm2
C.48cm2
D.96cm2
二、填空题(每小题3分,共30分)
11.(广东中考)正五边形的外角和为
.
12.在?ABCD中,若∠A∶∠B=1∶5,则∠D=
;若∠A+∠C=140°,则∠D=
.
13.如图,在△ABC中,点D、E分别是AB、AC的中点.若BC=6,则DE=
.
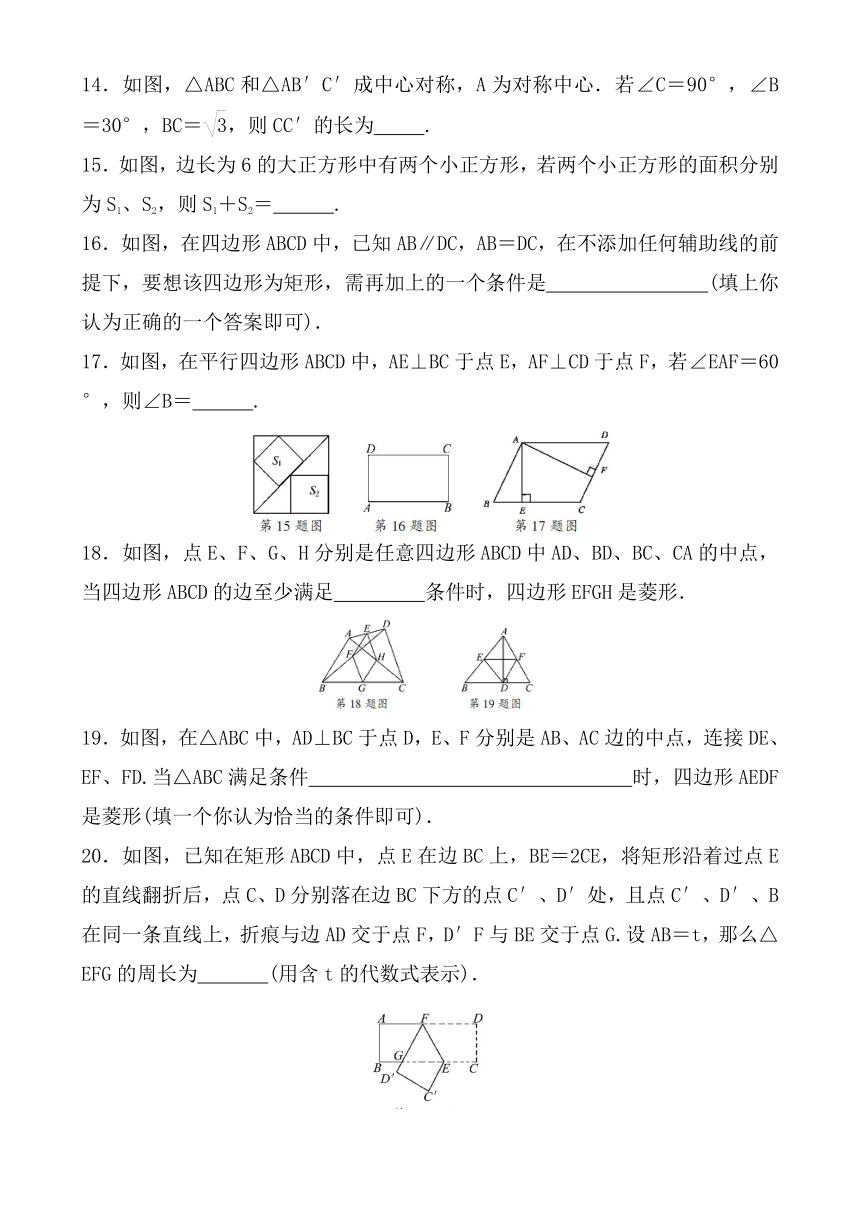
14.如图,△ABC和△AB′C′成中心对称,A为对称中心.若∠C=90°,∠B=30°,BC=,则CC′的长为
.
15.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2=
.
16.如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的前提下,要想该四边形为矩形,需再加上的一个条件是
(填上你认为正确的一个答案即可).
17.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=60°,则∠B=
.
18.如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足
条件时,四边形EFGH是菱形.
19.如图,在△ABC中,AD⊥BC于点D,E、F分别是AB、AC边的中点,连接DE、EF、FD.当△ABC满足条件
时,四边形AEDF是菱形(填一个你认为恰当的条件即可).
20.如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为
(用含t的代数式表示).
三、解答题(共60分)
21.(6分)如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF.
求证:BE=AF.
22.(8分)如图,已知?ABCD.
(1)画出?A1B1C1D1,使?A1B1C1D1与?ABCD关于直线MN对称;
(2)画出?A2B2C2D2,使?A2B2C2D2与?ABCD关于点O中心对称;
(3)?A1B1C1D1与?A2B2C2D2是对称图形吗?若是,请在图上画出对称轴或对称中心.
23.(8分)如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
24.(8分)如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
25.(10分)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为
时,四边形AMDN是矩形;②当AM的值为
时,四边形AMDN是菱形.
26.(10分)对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
27.(10分)在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图①,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图②,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图③,请你求出CF的长.
答案:
一、
1-10
BDBAB
CDBAB
二、
11.
360°
12.
150°
110°
13.
3
14.
2
15.
17
16.
答案不唯一,如∠A=90°等
17.
60°
18.
AB=CD
19.
答案不唯一,如AB=AC,BD=DC等
20.
2t
三、
21.
证明:∵四边形ABCD是正方形,∴AD=AB,∠D=∠EAB=90°,在△EAB和△FDA中,,∴△EAB≌△FDA(SAS),∴BE=AF.
22.
解:(1)如图,?A1B1C1D1即为所求;
(2)如图,?A2B2C2D2即为所求;
(3)是对称图形,对称轴是直线EF.
23.
(1)证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD.又∵BE∥AC,∴四边形ABEC是平行四边形.∴BE=AC,∴BD=BE;
(2)解:∵四边形ABCD是矩形,∴AO=OC=BO=OD=4,即BD=8.∵∠DBC=30°,∴∠ABO=90°-30°=60°.∴△ABO是等边三角形,即AB=OB=4,于是AB=DC=CE=4.在Rt△DBC中,DC=4,BD=8,BC==4.∵AB∥DE,AD与BE不平行,∴四边形ABED是梯形,且BC为梯形的高,∴四边形ABED的面积=·(AB+DE)·BC=·(4+4+4)·4=24.
24.
证明:(1)因为DE∥AC,DF∥AB,所以四边形AEDF是平行四边形,所以AE=DF;
(2)若AD平分∠BAC,四边形AEDF是菱形.证明:∵AD平分∠BAC,∴∠EAD=∠FAD,∵DE∥AC,∴∠ADE=∠FAD,∴∠EAD=∠ADE,∴AE=DE,∵四边形AEDF是平行四边形,∴AEDF为菱形.
25.
(1)证明:∵四边形ABCD是菱形,∴ND∥AM,∴∠NDE=∠MAE,∠DNE=∠AME,又∵点E是AD边的中点,∴DE=AE,∴△NDE≌△MAE,∴ND=MA,∴四边形AMDN是平行四边形.
(2)
1
2
26.
证明:(1)∵对折AD与BC重合,折痕是MN,∴点M是AB的中点,∴A′是EF的中点,∵∠BA′E=∠A=90°,∴BA′垂直平分EF,∴BE=BF,∴∠A′BE=∠A′BF,由翻折的性质,∠ABE=∠A′BE,∴∠ABE=∠A′BE=∠A′BF,∴∠ABE=×90°=30°;
(2)∵沿EA′所在的直线折叠,点B落在AD上的点B′处,∴BE=B′E,BF=B′F,∵BE=BF,∴BE=B′E=B′F=BF,∴四边形BFB′E为菱形.
27.
解:(1)AD=CF.理由:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF,在△AOD和△COF中,∴△AOD≌△COF(SAS),∴AD=CF;
(2)与(1)同理求出CF=AD,连接DF交OE于G,则DF⊥OE,DG=OG=OE,∵正方形ODEF的边长为,∴OE=×=2,∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4.在Rt△ADG中,AD===,∴CF=AD=.
(满分120分)
一、选择题(每小题3分,共30分)
1.平行四边形的对角线一定具有的性质是(
)
A.相等
B.互相平分
C.互相垂直
D.互相垂直且相等
2.下列手机软件图标中,既是轴对称图形又是中心对称图形的是(
)
3.一个多边形的内角和是360°,这个多边形是(
)
A.三角形
B.四边形
C.六边形
D.不能确定
4.如果三角形的两边分别为3和5,那么连接这个三角形三边中点所得三角形的周长可能是(
)
A.5.5
B.5
C.4.5
D.4
5.下列命题中正确的是(
)
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
6.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是(
)
A.1
B.
C.2
D.2
7.如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为(
)
A.
B.
C.5
D.
8.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为(
)
A.1
B.
C.2
D.
9.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图①,测得AC=2;当∠B=60°时,如图②,AC=(
)
A.
B.2
C.
D.2
10.一菱形的周长是20cm,两条对角线的比是4∶3,则菱形的面积是(
)
A.12cm2
B.24cm2
C.48cm2
D.96cm2
二、填空题(每小题3分,共30分)
11.(广东中考)正五边形的外角和为
.
12.在?ABCD中,若∠A∶∠B=1∶5,则∠D=
;若∠A+∠C=140°,则∠D=
.
13.如图,在△ABC中,点D、E分别是AB、AC的中点.若BC=6,则DE=
.
14.如图,△ABC和△AB′C′成中心对称,A为对称中心.若∠C=90°,∠B=30°,BC=,则CC′的长为
.
15.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2=
.
16.如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的前提下,要想该四边形为矩形,需再加上的一个条件是
(填上你认为正确的一个答案即可).
17.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=60°,则∠B=
.
18.如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足
条件时,四边形EFGH是菱形.
19.如图,在△ABC中,AD⊥BC于点D,E、F分别是AB、AC边的中点,连接DE、EF、FD.当△ABC满足条件
时,四边形AEDF是菱形(填一个你认为恰当的条件即可).
20.如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为
(用含t的代数式表示).
三、解答题(共60分)
21.(6分)如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF.
求证:BE=AF.
22.(8分)如图,已知?ABCD.
(1)画出?A1B1C1D1,使?A1B1C1D1与?ABCD关于直线MN对称;
(2)画出?A2B2C2D2,使?A2B2C2D2与?ABCD关于点O中心对称;
(3)?A1B1C1D1与?A2B2C2D2是对称图形吗?若是,请在图上画出对称轴或对称中心.
23.(8分)如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
24.(8分)如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
25.(10分)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为
时,四边形AMDN是矩形;②当AM的值为
时,四边形AMDN是菱形.
26.(10分)对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
27.(10分)在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图①,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图②,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图③,请你求出CF的长.
答案:
一、
1-10
BDBAB
CDBAB
二、
11.
360°
12.
150°
110°
13.
3
14.
2
15.
17
16.
答案不唯一,如∠A=90°等
17.
60°
18.
AB=CD
19.
答案不唯一,如AB=AC,BD=DC等
20.
2t
三、
21.
证明:∵四边形ABCD是正方形,∴AD=AB,∠D=∠EAB=90°,在△EAB和△FDA中,,∴△EAB≌△FDA(SAS),∴BE=AF.
22.
解:(1)如图,?A1B1C1D1即为所求;
(2)如图,?A2B2C2D2即为所求;
(3)是对称图形,对称轴是直线EF.
23.
(1)证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD.又∵BE∥AC,∴四边形ABEC是平行四边形.∴BE=AC,∴BD=BE;
(2)解:∵四边形ABCD是矩形,∴AO=OC=BO=OD=4,即BD=8.∵∠DBC=30°,∴∠ABO=90°-30°=60°.∴△ABO是等边三角形,即AB=OB=4,于是AB=DC=CE=4.在Rt△DBC中,DC=4,BD=8,BC==4.∵AB∥DE,AD与BE不平行,∴四边形ABED是梯形,且BC为梯形的高,∴四边形ABED的面积=·(AB+DE)·BC=·(4+4+4)·4=24.
24.
证明:(1)因为DE∥AC,DF∥AB,所以四边形AEDF是平行四边形,所以AE=DF;
(2)若AD平分∠BAC,四边形AEDF是菱形.证明:∵AD平分∠BAC,∴∠EAD=∠FAD,∵DE∥AC,∴∠ADE=∠FAD,∴∠EAD=∠ADE,∴AE=DE,∵四边形AEDF是平行四边形,∴AEDF为菱形.
25.
(1)证明:∵四边形ABCD是菱形,∴ND∥AM,∴∠NDE=∠MAE,∠DNE=∠AME,又∵点E是AD边的中点,∴DE=AE,∴△NDE≌△MAE,∴ND=MA,∴四边形AMDN是平行四边形.
(2)
1
2
26.
证明:(1)∵对折AD与BC重合,折痕是MN,∴点M是AB的中点,∴A′是EF的中点,∵∠BA′E=∠A=90°,∴BA′垂直平分EF,∴BE=BF,∴∠A′BE=∠A′BF,由翻折的性质,∠ABE=∠A′BE,∴∠ABE=∠A′BE=∠A′BF,∴∠ABE=×90°=30°;
(2)∵沿EA′所在的直线折叠,点B落在AD上的点B′处,∴BE=B′E,BF=B′F,∵BE=BF,∴BE=B′E=B′F=BF,∴四边形BFB′E为菱形.
27.
解:(1)AD=CF.理由:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF,在△AOD和△COF中,∴△AOD≌△COF(SAS),∴AD=CF;
(2)与(1)同理求出CF=AD,连接DF交OE于G,则DF⊥OE,DG=OG=OE,∵正方形ODEF的边长为,∴OE=×=2,∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4.在Rt△ADG中,AD===,∴CF=AD=.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
