2020—2021学年八年级数学人教版下册18.2.3正方形课件(21张)
文档属性
| 名称 | 2020—2021学年八年级数学人教版下册18.2.3正方形课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 688.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:28:23 | ||
图片预览





文档简介
(共21张PPT)
18.2.3正方形
正方形的判定
学习目标
1.掌握正方形的判定条件.(重点)
2.会运用正方形的判定条件进行有关的论证.(难点)
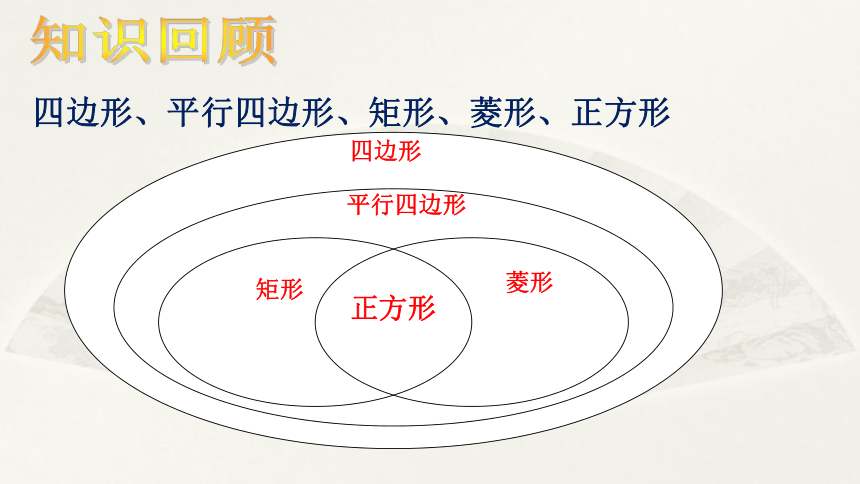
四边形、平行四边形、矩形、菱形、正方形
四边形
平行四边形
矩形
菱形
正方形
知识回顾
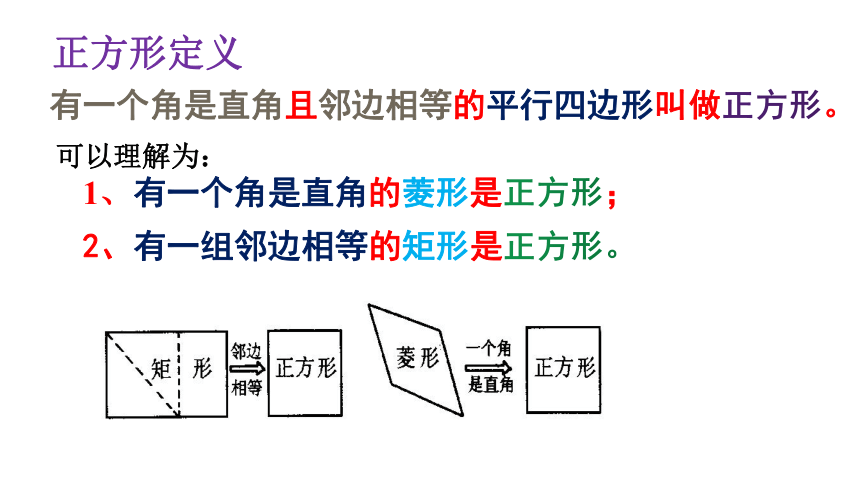
正方形定义
有一个角是直角且邻边相等的平行四边形叫做正方形。
可以理解为:
1、有一个角是直角的菱形是正方形;
2、有一组邻边相等的矩形是正方形。
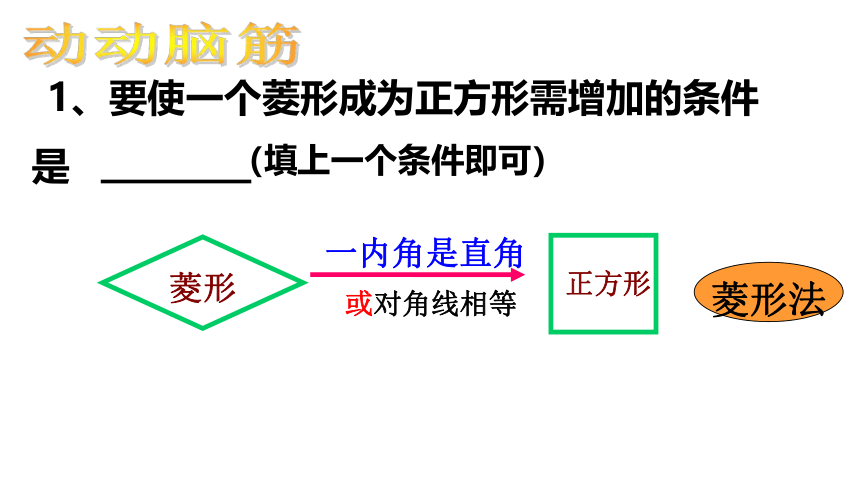
1、要使一个菱形成为正方形需增加的条件
是
(填上一个条件即可)
动动脑筋
正方形
菱形
一内角是直角
或对角线相等
菱形法
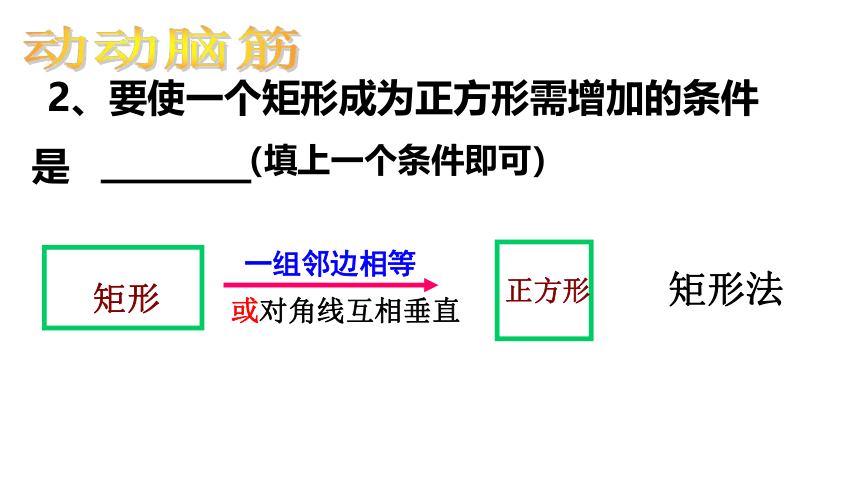
2、要使一个矩形成为正方形需增加的条件
是
(填上一个条件即可)
动动脑筋
或对角线互相垂直
矩形
一组邻边相等
正方形
矩形法
平行四边形
正方形
一组邻边相等
且一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
定义法
菱形法
矩形法
或对角线相等
或对角线互相垂直
√
√
√
×
(1)对角线互相垂直且相等的四边形是正方形(
)
(2)如果一个菱形的对角线相等,那么它一定
是正方形
(
)
(3)如果一个矩形的对角线互相垂直,那么它
一定是正方形
(
)
(4)四条边相等,且有一个角是直角的四边形
是正方形(
)
(5)四个角都相等的四边形是正方形
(
)
(6)四条边都相等的四边形是正方形
(
)
判断题:
×
×
课堂练习1:
.已知四边形ABCD是平行四边形,对角线AC、BD相交于点O。
⑴若AB=BC,则四边形ABCD是(
)
⑵若AC=BD,则四边形ABCD是(
)
⑶若∠BCD=900,则四边形ABCD是(
)
⑷若OA=OB,则四边形ABCD是(
)
⑸若AB=BC,且AC=BD,则四边形ABCD是
(
)
菱形
矩形
矩形
矩形
正方形
课堂练习2:
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是(
)
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
C
A
B
C
D
O
课堂练习3:
例题分析
例1、直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB
求证:四边形CEDF是正方形。
例题分析:
例题分析
例题分析:
A
B
C
D
E
F
∴四边形CEDF是正方形(
)
∴
DE=DF(
)
且DE⊥AC,
DF⊥BC
∵
CD平分∠ACB
∴
四边形CEDF为矩形(
)
而∠ACB=90°
∴
∠DEC=90°,
∠DFC=90°
证明:∵
DE⊥AC,DF⊥AB
有三个角是直角的四边形是矩形
角平分线上的点到角两边的距离相等
有一组邻边相等的矩形是正方形
例题分析
例2.正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.
四边形A`B`C`D`是正方形吗?为什么?
例题分析:
例题分析
例题分析:
在正方形ABCD中,点A`,B`,C`,D`分别是AB,BC,CD,DA的中点,
四边形A`B`C`D`是正方形吗?为什么?
课堂练习:
课堂练习:
四边形
平行四边形
矩形
菱形
正方形
课堂小结:
5种判
定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.矩形ABCD中,四个内角的平分线组成四边形EMFN,判断四边形EMFN的形状,并说明原因。
课后练习:
课后练习:
18.2.3正方形
正方形的判定
学习目标
1.掌握正方形的判定条件.(重点)
2.会运用正方形的判定条件进行有关的论证.(难点)
四边形、平行四边形、矩形、菱形、正方形
四边形
平行四边形
矩形
菱形
正方形
知识回顾
正方形定义
有一个角是直角且邻边相等的平行四边形叫做正方形。
可以理解为:
1、有一个角是直角的菱形是正方形;
2、有一组邻边相等的矩形是正方形。
1、要使一个菱形成为正方形需增加的条件
是
(填上一个条件即可)
动动脑筋
正方形
菱形
一内角是直角
或对角线相等
菱形法
2、要使一个矩形成为正方形需增加的条件
是
(填上一个条件即可)
动动脑筋
或对角线互相垂直
矩形
一组邻边相等
正方形
矩形法
平行四边形
正方形
一组邻边相等
且一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
定义法
菱形法
矩形法
或对角线相等
或对角线互相垂直
√
√
√
×
(1)对角线互相垂直且相等的四边形是正方形(
)
(2)如果一个菱形的对角线相等,那么它一定
是正方形
(
)
(3)如果一个矩形的对角线互相垂直,那么它
一定是正方形
(
)
(4)四条边相等,且有一个角是直角的四边形
是正方形(
)
(5)四个角都相等的四边形是正方形
(
)
(6)四条边都相等的四边形是正方形
(
)
判断题:
×
×
课堂练习1:
.已知四边形ABCD是平行四边形,对角线AC、BD相交于点O。
⑴若AB=BC,则四边形ABCD是(
)
⑵若AC=BD,则四边形ABCD是(
)
⑶若∠BCD=900,则四边形ABCD是(
)
⑷若OA=OB,则四边形ABCD是(
)
⑸若AB=BC,且AC=BD,则四边形ABCD是
(
)
菱形
矩形
矩形
矩形
正方形
课堂练习2:
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是(
)
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
C
A
B
C
D
O
课堂练习3:
例题分析
例1、直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB
求证:四边形CEDF是正方形。
例题分析:
例题分析
例题分析:
A
B
C
D
E
F
∴四边形CEDF是正方形(
)
∴
DE=DF(
)
且DE⊥AC,
DF⊥BC
∵
CD平分∠ACB
∴
四边形CEDF为矩形(
)
而∠ACB=90°
∴
∠DEC=90°,
∠DFC=90°
证明:∵
DE⊥AC,DF⊥AB
有三个角是直角的四边形是矩形
角平分线上的点到角两边的距离相等
有一组邻边相等的矩形是正方形
例题分析
例2.正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.
四边形A`B`C`D`是正方形吗?为什么?
例题分析:
例题分析
例题分析:
在正方形ABCD中,点A`,B`,C`,D`分别是AB,BC,CD,DA的中点,
四边形A`B`C`D`是正方形吗?为什么?
课堂练习:
课堂练习:
四边形
平行四边形
矩形
菱形
正方形
课堂小结:
5种判
定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.矩形ABCD中,四个内角的平分线组成四边形EMFN,判断四边形EMFN的形状,并说明原因。
课后练习:
课后练习:
