2020-2021学年北师大版数学七年级下册2.3.1平行线的性质探究课件(20张PPT)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册2.3.1平行线的性质探究课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
北师大版七年级下册
2.3
平行线的性质
(第1课时)
c
a
b
2
1
3
4
6
5
7
8
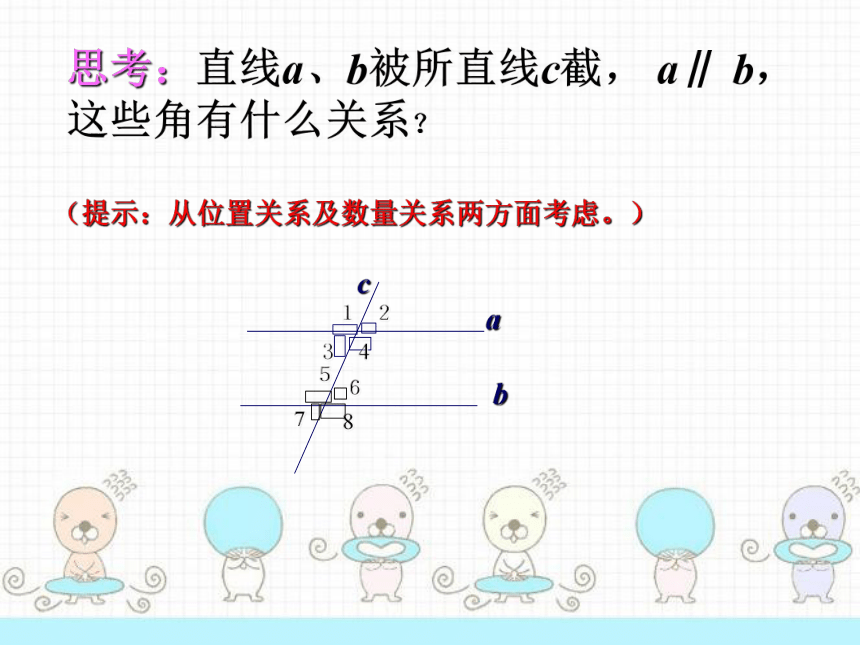
思考:直线a、b被所直线c截,
a∥
b,这些角有什么关系?
(提示:从位置关系及数量关系两方面考虑。)
b
1
2
3
4
5
6
7
8
a
c
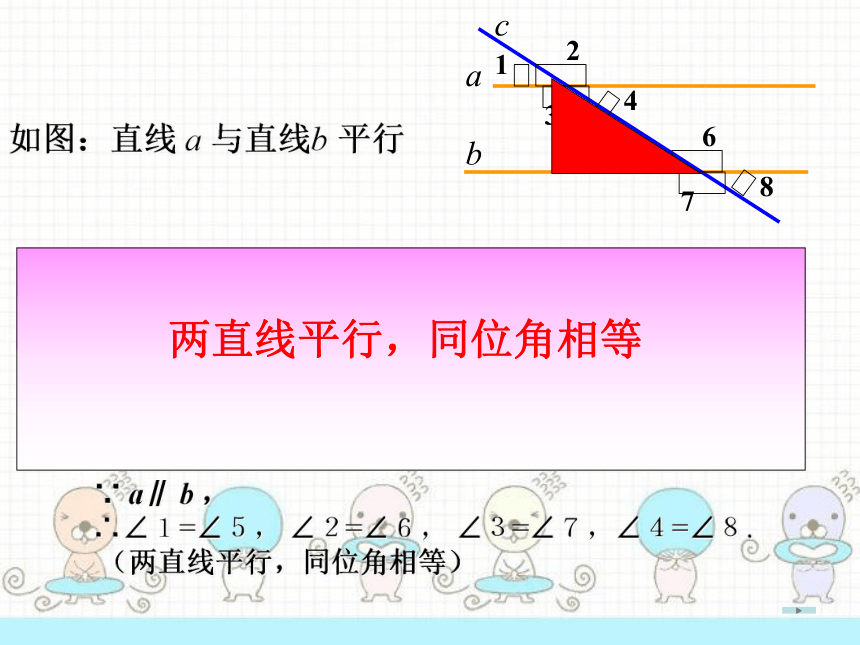
如图:直线
a
与直线b
平行
两直线平行,同位角相等
∵
a∥
b
,
∴∠1=∠5,
∠2=∠6,
∠3=∠7,∠4=∠8.
(两直线平行,同位角相等)
b
1
2
3
4
5
6
7
8
a
c
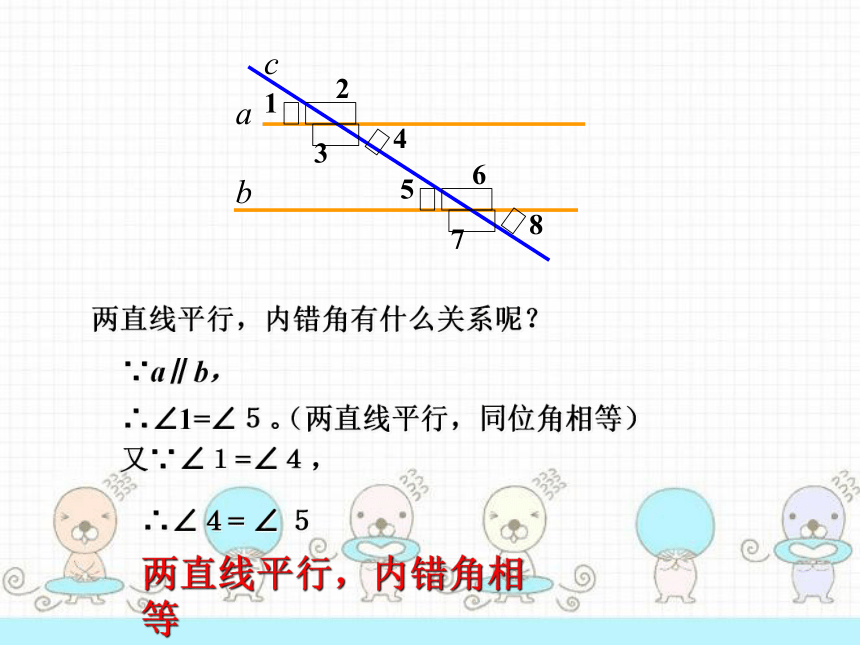
两直线平行,内错角有什么关系呢?
两直线平行,内错角相等
∵a∥b,
∴∠1=∠5。
(两直线平行,同位角相等)
又∵∠1=∠4,
∴∠4=
∠
5
b
1
2
3
4
5
6
7
8
a
c
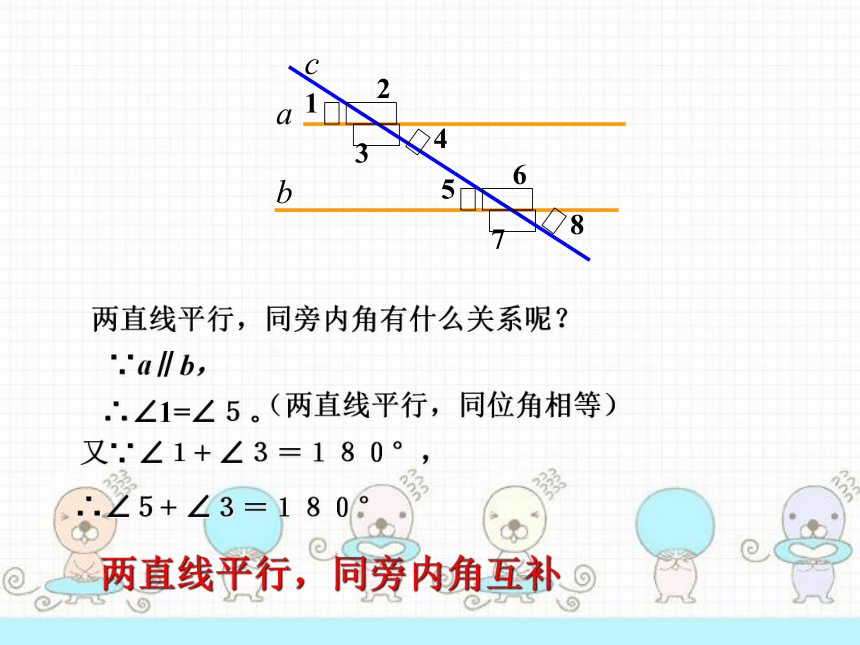
两直线平行,同旁内角有什么关系呢?
∴∠5+
∠3=180°
两直线平行,同旁内角互补
∵a∥b,
∴∠1=∠5。
(两直线平行,同位角相等)
又∵∠1+
∠3=180°,
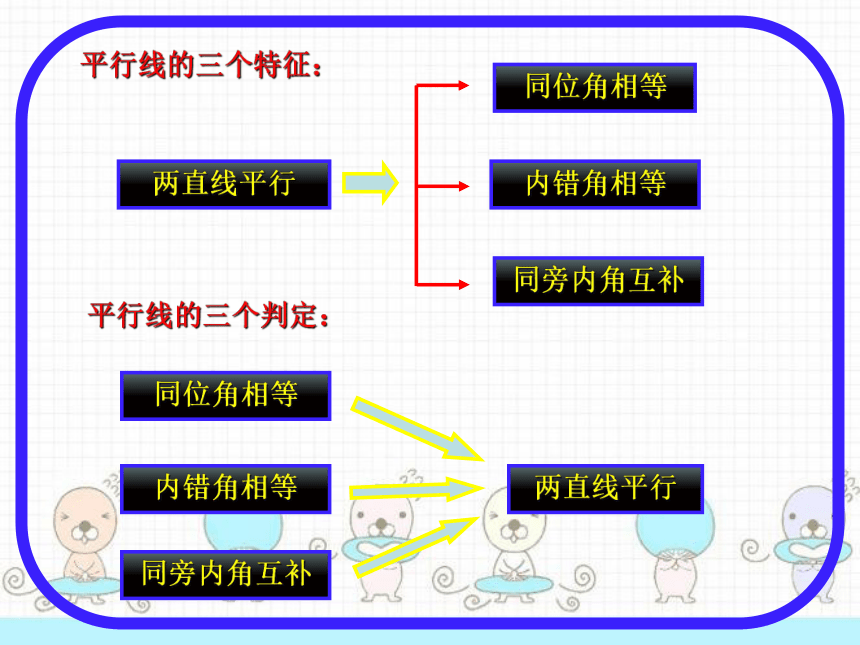
平行线的三个特征:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
例1
如图,已知直线a∥b,
∠1=50°,求∠5的度数。
两条平行线被第三条直线所截的八个角,
已知一个,可以求出其余的七个角。
b
4
3
1
2
5
6
7
8
a
c
能够求图中的其余所有角吗?
解: ∵
a∥b,
∴
∠1+∠5=180°
(两直线平行,同旁内角互补)
∴
∠5=
180°-
∠1
=130°
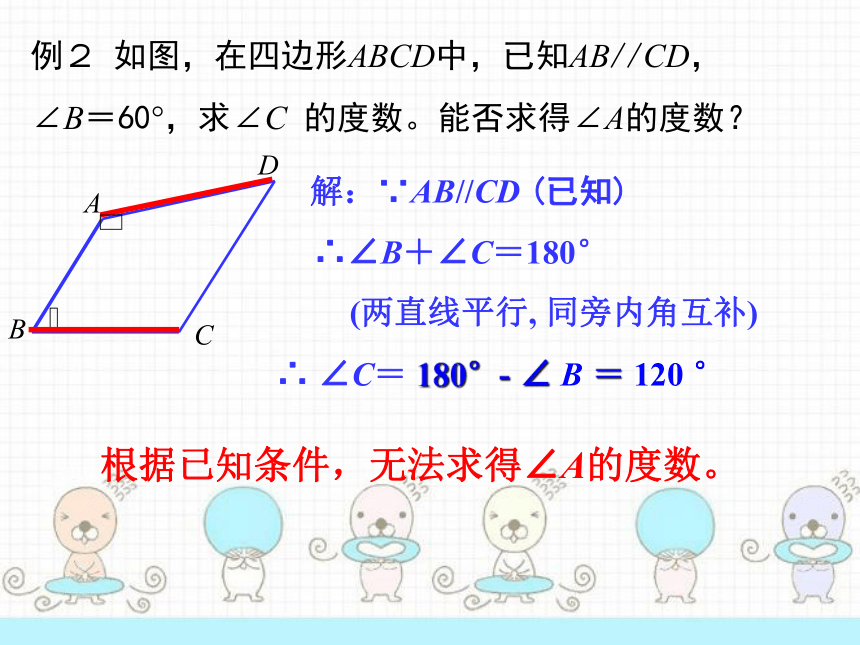
例2
如图,在四边形ABCD中,已知AB//CD,
∠B=60?,求∠C
的度数。能否求得∠A的度数?
A
B
C
D
解:∵AB//CD
(已知)
∴∠B+∠C=180°
(两直线平行,
同旁内角互补)
∴
∠C=
180°-
∠
B
=
120
°
根据已知条件,无法求得∠A的度数。
A
B
C
D
E
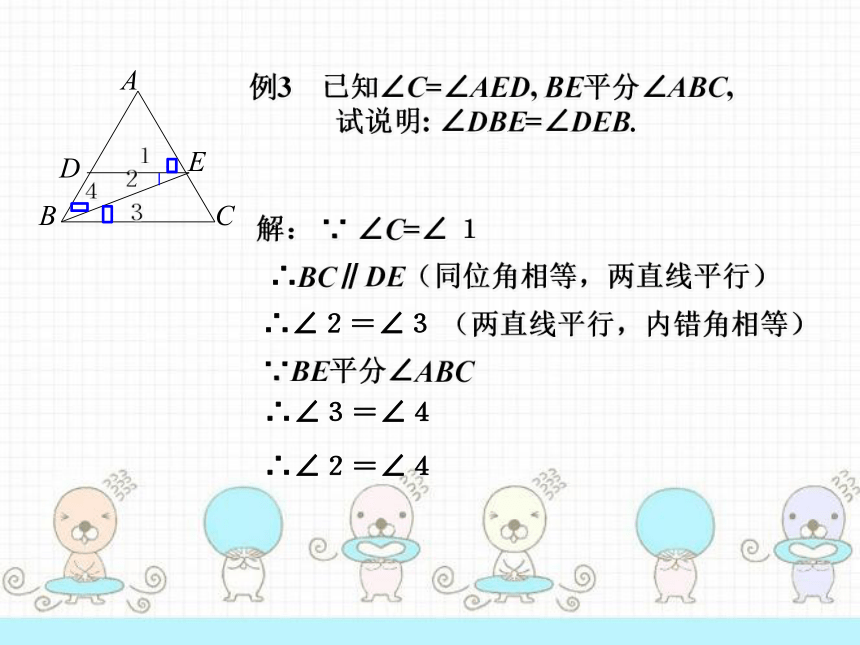
例3 已知∠C=∠AED,
BE平分∠ABC,
试说明:
∠DBE=∠DEB.
1
2
3
4
解:
∵
∠C=∠
1
∴BC∥DE(同位角相等,两直线平行)
∴∠2=∠3
(两直线平行,内错角相等)
∵BE平分∠ABC
∴∠3=∠4
∴∠2=∠4
1.如图,已知:∠1+∠2=180°.
求证:AB∥CD.
证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等)
∠2=∠4(
)
根据:等量代换
得:∠3+
=180°.
根据:同旁内角互补,两直线平行
得:
∥
.
4
1
2
3
A
B
C
E
F
D
对顶角相等
∠4
AB
CD
变式.
已知:
AB∥CD.
求证:
∠1+∠2=180°.
证明:由:
AB∥CD
(已知)
得∠3+∠4=180°(
?)
根据:∠2=∠4(
)
∠1=∠3
得:∠1+
=180°(
?)
4
1
2
3
A
B
C
E
F
D
对顶角相等
∠2
(等量代换)
(两直线平行,同旁内角互补)
(思维拓展)已知:
AB∥CD
你能确定∠B、∠D、∠E的数量关系吗?
平行线的三个特征:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
课后作业
(1)看书P21—P23(补全书上留白,划出重点内容);
(2)书P25习题5.3第1—6题;
(3)探究题(选作)
已知:∠M=135°,∠T
=
85°
,∠P=
140°.
你能判定MN∥PQ吗?
M
N
P
Q
T
爱学数学
爱数学周报
再见
北师大版七年级下册
2.3
平行线的性质
(第1课时)
c
a
b
2
1
3
4
6
5
7
8
思考:直线a、b被所直线c截,
a∥
b,这些角有什么关系?
(提示:从位置关系及数量关系两方面考虑。)
b
1
2
3
4
5
6
7
8
a
c
如图:直线
a
与直线b
平行
两直线平行,同位角相等
∵
a∥
b
,
∴∠1=∠5,
∠2=∠6,
∠3=∠7,∠4=∠8.
(两直线平行,同位角相等)
b
1
2
3
4
5
6
7
8
a
c
两直线平行,内错角有什么关系呢?
两直线平行,内错角相等
∵a∥b,
∴∠1=∠5。
(两直线平行,同位角相等)
又∵∠1=∠4,
∴∠4=
∠
5
b
1
2
3
4
5
6
7
8
a
c
两直线平行,同旁内角有什么关系呢?
∴∠5+
∠3=180°
两直线平行,同旁内角互补
∵a∥b,
∴∠1=∠5。
(两直线平行,同位角相等)
又∵∠1+
∠3=180°,
平行线的三个特征:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
例1
如图,已知直线a∥b,
∠1=50°,求∠5的度数。
两条平行线被第三条直线所截的八个角,
已知一个,可以求出其余的七个角。
b
4
3
1
2
5
6
7
8
a
c
能够求图中的其余所有角吗?
解: ∵
a∥b,
∴
∠1+∠5=180°
(两直线平行,同旁内角互补)
∴
∠5=
180°-
∠1
=130°
例2
如图,在四边形ABCD中,已知AB//CD,
∠B=60?,求∠C
的度数。能否求得∠A的度数?
A
B
C
D
解:∵AB//CD
(已知)
∴∠B+∠C=180°
(两直线平行,
同旁内角互补)
∴
∠C=
180°-
∠
B
=
120
°
根据已知条件,无法求得∠A的度数。
A
B
C
D
E
例3 已知∠C=∠AED,
BE平分∠ABC,
试说明:
∠DBE=∠DEB.
1
2
3
4
解:
∵
∠C=∠
1
∴BC∥DE(同位角相等,两直线平行)
∴∠2=∠3
(两直线平行,内错角相等)
∵BE平分∠ABC
∴∠3=∠4
∴∠2=∠4
1.如图,已知:∠1+∠2=180°.
求证:AB∥CD.
证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等)
∠2=∠4(
)
根据:等量代换
得:∠3+
=180°.
根据:同旁内角互补,两直线平行
得:
∥
.
4
1
2
3
A
B
C
E
F
D
对顶角相等
∠4
AB
CD
变式.
已知:
AB∥CD.
求证:
∠1+∠2=180°.
证明:由:
AB∥CD
(已知)
得∠3+∠4=180°(
?)
根据:∠2=∠4(
)
∠1=∠3
得:∠1+
=180°(
?)
4
1
2
3
A
B
C
E
F
D
对顶角相等
∠2
(等量代换)
(两直线平行,同旁内角互补)
(思维拓展)已知:
AB∥CD
你能确定∠B、∠D、∠E的数量关系吗?
平行线的三个特征:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
课后作业
(1)看书P21—P23(补全书上留白,划出重点内容);
(2)书P25习题5.3第1—6题;
(3)探究题(选作)
已知:∠M=135°,∠T
=
85°
,∠P=
140°.
你能判定MN∥PQ吗?
M
N
P
Q
T
爱学数学
爱数学周报
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
