2020—2021学年沪科版数学八年级下册课件-18.1 勾股定理(22张)
文档属性
| 名称 | 2020—2021学年沪科版数学八年级下册课件-18.1 勾股定理(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 519.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 15:04:14 | ||
图片预览



文档简介
(共22张PPT)
18.1
勾股定理
探究:
下面就让我们通过时光隧道,和古希腊的数学家毕达哥拉斯一起来研究这种图形吧。
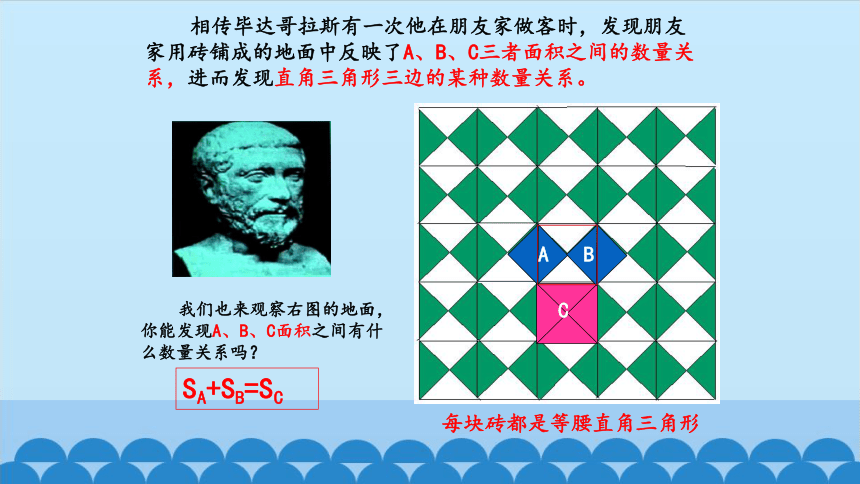
相传毕达哥拉斯有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系。
A
B
C
我们也来观察右图的地面,你能发现A、B、C面积之间有什么数量关系吗?
SA+SB=SC
每块砖都是等腰直角三角形
A
B
C
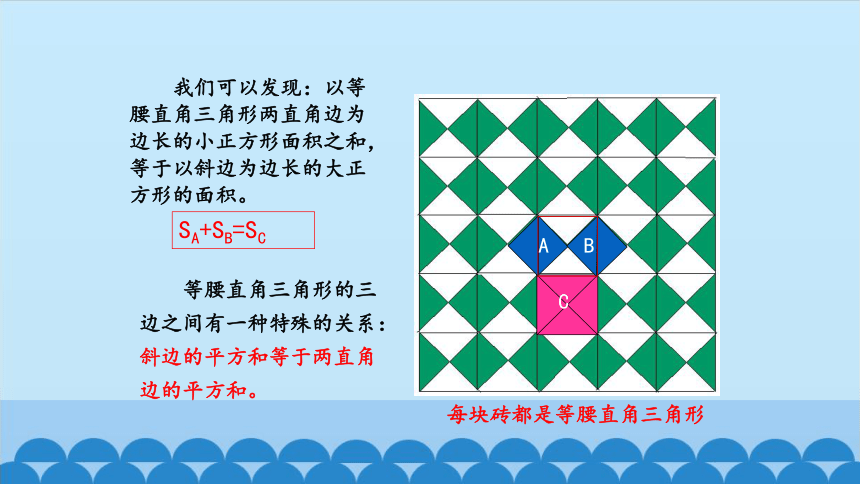
等腰直角三角形的三边之间有一种特殊的关系:斜边的平方和等于两直角边的平方和。
SA+SB=SC
每块砖都是等腰直角三角形
我们可以发现:以等腰直角三角形两直角边为边长的小正方形面积之和,等于以斜边为边长的大正方形的面积。
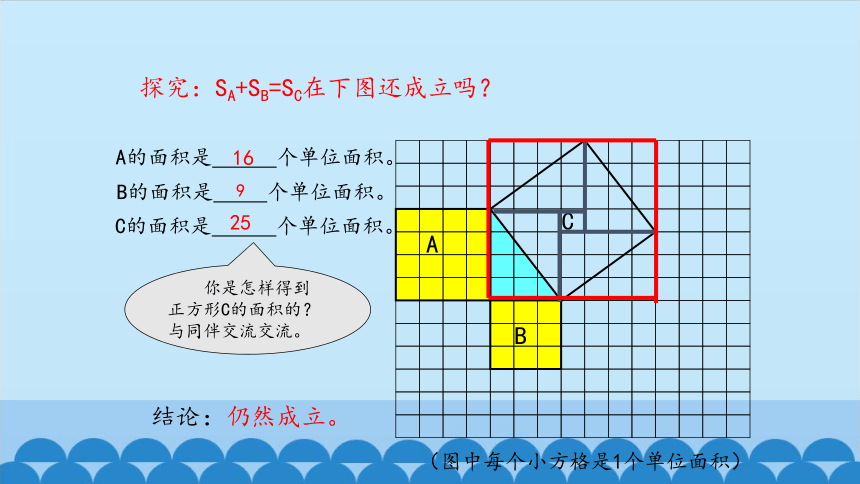
探究:SA+SB=SC在下图还成立吗?
A
B
C
结论:仍然成立。
A的面积是
个单位面积。
B的面积是
个单位面积。
C的面积是
个单位面积。
25
16
9
你是怎样得到正方形C的面积的?与同伴交流交流。
(图中每个小方格是1个单位面积)
A
B
C
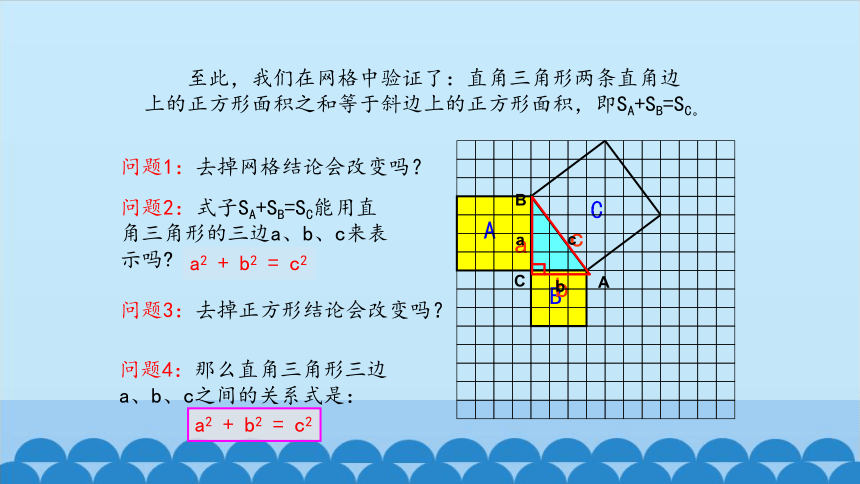
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?
问题4:那么直角三角形三边a、b、c之间的关系式是:
a
b
c
至此,我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC。
a2
+
b2
=
c2
a2
+
b2
=
c2
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
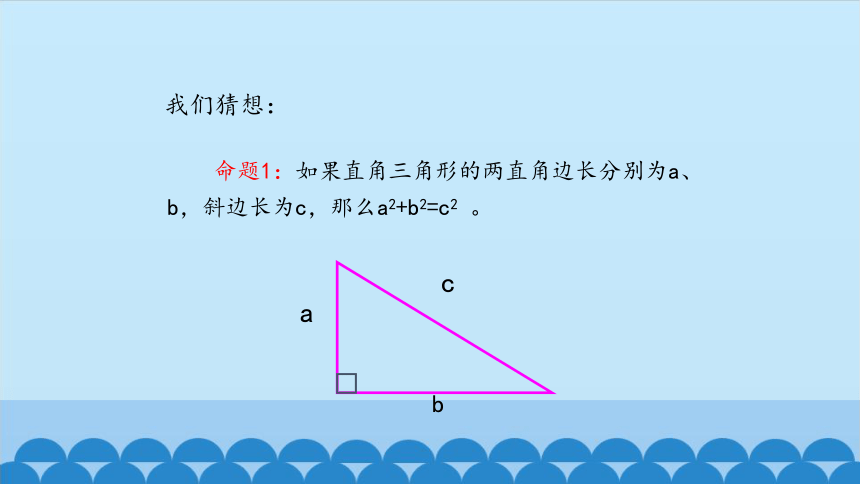
命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2
。
a
b
c
我们猜想:
是不是所有的直角三角形都具有这样的结论呢?光靠实验和猜想还不能把问题彻底搞清楚。
这就需要我们对一般的直角三角形进行证明。下面我们就一起来探究,看一看我国古代数学家赵爽是怎样证明这个命题的。
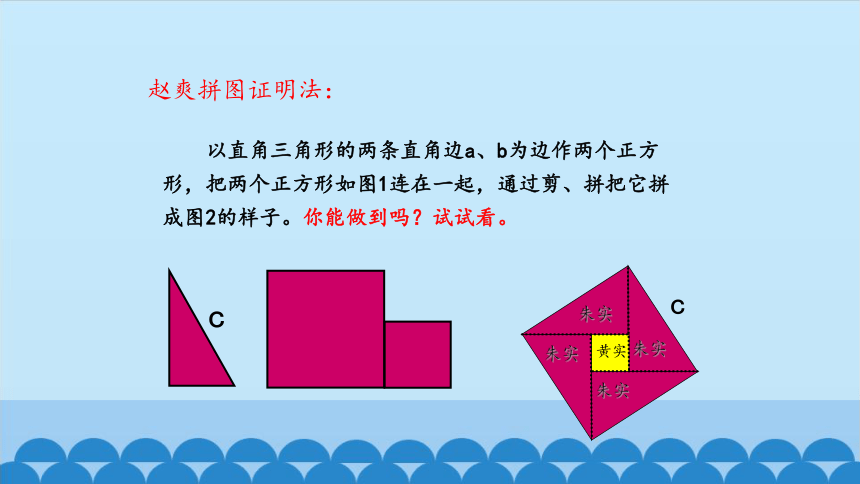
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子。你能做到吗?试试看。
赵爽拼图证明法:
c
黄实
朱实
朱实
朱实
朱实
c
黄实
朱实
朱实
朱实
朱实
b
?
a
〓
M
N
P
剪、拼过程展示:
“赵爽弦图”
黄实
朱实
朱实
朱实
朱实
c
a
b
c
b
a
用赵爽弦图证明
=
b
a
现在,我们已经证明了命题1的正确性,在数学上,经过证明被确认为正确的命题叫做定理,所以命题1在我国叫做勾股定理。
即:直角三角形两直角边的平方和等于斜边的平方。
勾股定理:
如果直角三角形两直角边长分别为a、b,斜边长为c,那么a2+b2=c2
。
a
b
c
例1:如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
例题探究:
9m
24m
?
例2:现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图,已知云梯最多只能伸长到10m,消防车高3m。救人时云梯伸至最长,在完成9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
设AC=x,则OC=8-x,于是根据勾股定理,得
从而可以解出x。
分析:如图,设A是云梯的下端点,AB是伸长后的云梯的,B是第一次救人的地点,D的第二次救人的地点,过点A的水平线与楼房ED的交点为O。则OB=9-3=6(m),OD=12-3=9(m)。
根据勾股定理得
解方程,得AO=8(m)
例3:已知:如图,在Rt△ABC中,两直角边AC=5,BC=12。求斜边上的高CD的长。
解:在Rt△ABC中,
又∵
Rt△ABC的面积
巩固练习
1.在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b。
(1)a=6,b=8,求c;
(2)a=8,c=17,求b。
2.在Rt△ABC中,∠B=90°,a=3,b=4,求c。
3.在直角三角形中,已知两边的长为3和4,求第三边的长。
运用勾股定理时应注意:
(1)在直角三角形中,认准直角边和斜边;
(2)两直角边的平方和等于斜边的平方。
4.图中已知数据表示面积,求表示边的未知数x、y的值。
9
16
x
y
144
169
5.
已知S1=1,S2=3,
S3=2,S4=4
,
求S5
、S6
、S7的值。
s3
1.本节课我们学到了什么?
通过学习,我们知道了著名的勾股定理,掌握了从特殊到一般的探索方法,还学会到了拼图证明的方法。
2.学了本节课后我们有什么感想?
我们发现有些数学结论就存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现。
谢
谢
18.1
勾股定理
探究:
下面就让我们通过时光隧道,和古希腊的数学家毕达哥拉斯一起来研究这种图形吧。
相传毕达哥拉斯有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系。
A
B
C
我们也来观察右图的地面,你能发现A、B、C面积之间有什么数量关系吗?
SA+SB=SC
每块砖都是等腰直角三角形
A
B
C
等腰直角三角形的三边之间有一种特殊的关系:斜边的平方和等于两直角边的平方和。
SA+SB=SC
每块砖都是等腰直角三角形
我们可以发现:以等腰直角三角形两直角边为边长的小正方形面积之和,等于以斜边为边长的大正方形的面积。
探究:SA+SB=SC在下图还成立吗?
A
B
C
结论:仍然成立。
A的面积是
个单位面积。
B的面积是
个单位面积。
C的面积是
个单位面积。
25
16
9
你是怎样得到正方形C的面积的?与同伴交流交流。
(图中每个小方格是1个单位面积)
A
B
C
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?
问题4:那么直角三角形三边a、b、c之间的关系式是:
a
b
c
至此,我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC。
a2
+
b2
=
c2
a2
+
b2
=
c2
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2
。
a
b
c
我们猜想:
是不是所有的直角三角形都具有这样的结论呢?光靠实验和猜想还不能把问题彻底搞清楚。
这就需要我们对一般的直角三角形进行证明。下面我们就一起来探究,看一看我国古代数学家赵爽是怎样证明这个命题的。
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子。你能做到吗?试试看。
赵爽拼图证明法:
c
黄实
朱实
朱实
朱实
朱实
c
黄实
朱实
朱实
朱实
朱实
b
?
a
〓
M
N
P
剪、拼过程展示:
“赵爽弦图”
黄实
朱实
朱实
朱实
朱实
c
a
b
c
b
a
用赵爽弦图证明
=
b
a
现在,我们已经证明了命题1的正确性,在数学上,经过证明被确认为正确的命题叫做定理,所以命题1在我国叫做勾股定理。
即:直角三角形两直角边的平方和等于斜边的平方。
勾股定理:
如果直角三角形两直角边长分别为a、b,斜边长为c,那么a2+b2=c2
。
a
b
c
例1:如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
例题探究:
9m
24m
?
例2:现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图,已知云梯最多只能伸长到10m,消防车高3m。救人时云梯伸至最长,在完成9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
设AC=x,则OC=8-x,于是根据勾股定理,得
从而可以解出x。
分析:如图,设A是云梯的下端点,AB是伸长后的云梯的,B是第一次救人的地点,D的第二次救人的地点,过点A的水平线与楼房ED的交点为O。则OB=9-3=6(m),OD=12-3=9(m)。
根据勾股定理得
解方程,得AO=8(m)
例3:已知:如图,在Rt△ABC中,两直角边AC=5,BC=12。求斜边上的高CD的长。
解:在Rt△ABC中,
又∵
Rt△ABC的面积
巩固练习
1.在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b。
(1)a=6,b=8,求c;
(2)a=8,c=17,求b。
2.在Rt△ABC中,∠B=90°,a=3,b=4,求c。
3.在直角三角形中,已知两边的长为3和4,求第三边的长。
运用勾股定理时应注意:
(1)在直角三角形中,认准直角边和斜边;
(2)两直角边的平方和等于斜边的平方。
4.图中已知数据表示面积,求表示边的未知数x、y的值。
9
16
x
y
144
169
5.
已知S1=1,S2=3,
S3=2,S4=4
,
求S5
、S6
、S7的值。
s3
1.本节课我们学到了什么?
通过学习,我们知道了著名的勾股定理,掌握了从特殊到一般的探索方法,还学会到了拼图证明的方法。
2.学了本节课后我们有什么感想?
我们发现有些数学结论就存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现。
谢
谢
