10.5(1)可化成一元一次方程的分式方程
文档属性
| 名称 | 10.5(1)可化成一元一次方程的分式方程 |

|
|
| 格式 | rar | ||
| 文件大小 | 137.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-07 00:00:00 | ||
图片预览




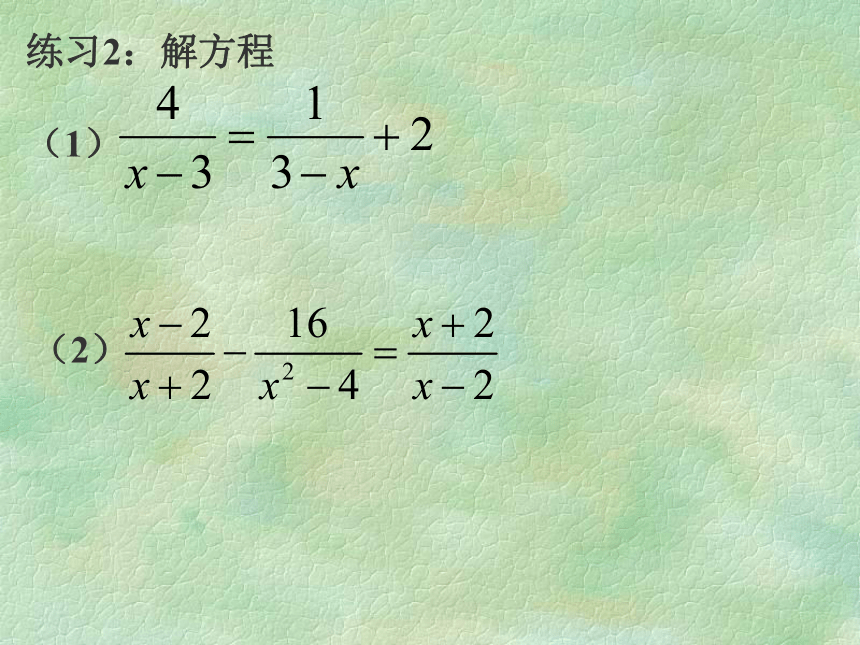
文档简介
(共15张PPT)
10.5(1)
可化成一元一次方程的分式方程
引例1:小杰和小莉两人从相距400米的两地同时
出发相向而行,练习跑步和竞走,
小杰每分钟跑320米,小莉每分钟走120米,
(1)若设两人x分钟后相遇,
则可列得方程: ;
(2)若设两人在相距A地x米处相遇,
则可列得方程: .
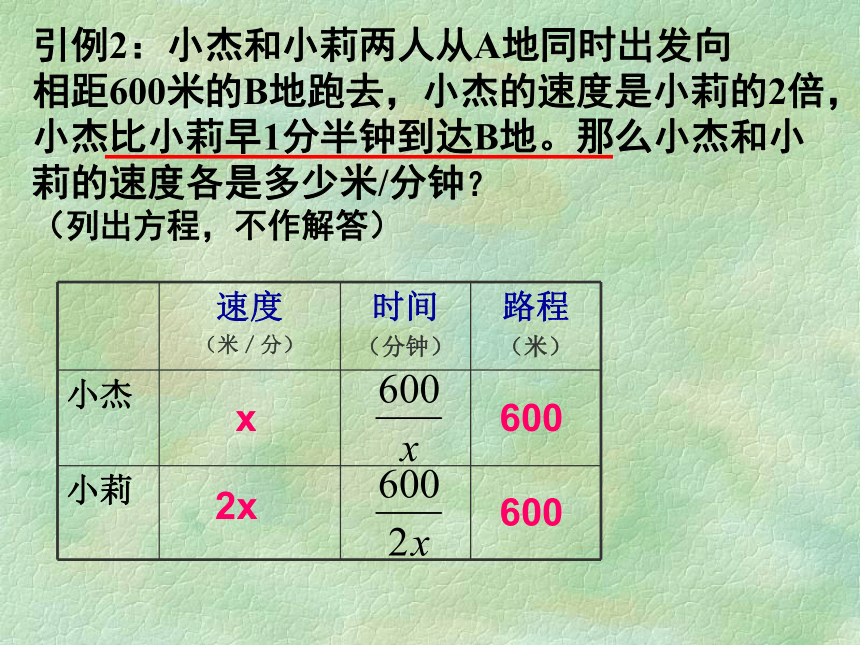
引例2:小杰和小莉两人从A地同时出发向
相距600米的B地跑去,小杰的速度是小莉的2倍,小杰比小莉早1分半钟到达B地。那么小杰和小莉的速度各是多少米/分钟?
(列出方程,不作解答)
速度
(米/分) 时间
(分钟) 路程
(米)
小杰
小莉
600
600
x
2x
判断下列哪些方程是分式方程?
(1)
(2)
(3)
(4)
(5)
(6)
练习1:x=2是下列哪个分式方程的一个解?
(1)
(2)
(3)
(1)解:把x=2代入原方程
左边=
右边=
因为 左边=右边
所以 x=2是原方程的一个解.
(3)解:把x=2代入原方程
结果使方程中的分式的分母为零,
分式无意义.
所以 x=2 不是原方程的解.
练习2:解方程
(1)
(2)
练习2:解方程
(2)
解:方程两边同乘以
检验:把x=2代入 x2-4,得x2-4=0。
所以 x=2是增根,不是原方程的解.
所以 原方程无解.
注意:分式方程的求根过程不一定是同解变形,所以分式方程一定要验根!
移项,化简得 x=2
引例2:小杰和小莉两人从A地同时出发向相距600米的B地跑去,小杰的速度是小莉的2倍,小杰比小莉早1分半钟到达B地。那么小杰和小莉的速度各是多少?
解分式方程的步骤:
(1)化:去分母,化成整式方程;
(2)解:解整式方程(一元一次方程);
(3)验:检验(可能产生増根).
课堂小结
思考题
则増根是 ,m为 .
有増根,
分式方程
作业布置
练习册P52-53 习题 10.5
课堂小结
分式方程
整式方程
转化
去分母
解
方
程
求整式方程的解
求分式方程的解
检验
10.5(1)
可化成一元一次方程的分式方程
引例1:小杰和小莉两人从相距400米的两地同时
出发相向而行,练习跑步和竞走,
小杰每分钟跑320米,小莉每分钟走120米,
(1)若设两人x分钟后相遇,
则可列得方程: ;
(2)若设两人在相距A地x米处相遇,
则可列得方程: .
引例2:小杰和小莉两人从A地同时出发向
相距600米的B地跑去,小杰的速度是小莉的2倍,小杰比小莉早1分半钟到达B地。那么小杰和小莉的速度各是多少米/分钟?
(列出方程,不作解答)
速度
(米/分) 时间
(分钟) 路程
(米)
小杰
小莉
600
600
x
2x
判断下列哪些方程是分式方程?
(1)
(2)
(3)
(4)
(5)
(6)
练习1:x=2是下列哪个分式方程的一个解?
(1)
(2)
(3)
(1)解:把x=2代入原方程
左边=
右边=
因为 左边=右边
所以 x=2是原方程的一个解.
(3)解:把x=2代入原方程
结果使方程中的分式的分母为零,
分式无意义.
所以 x=2 不是原方程的解.
练习2:解方程
(1)
(2)
练习2:解方程
(2)
解:方程两边同乘以
检验:把x=2代入 x2-4,得x2-4=0。
所以 x=2是增根,不是原方程的解.
所以 原方程无解.
注意:分式方程的求根过程不一定是同解变形,所以分式方程一定要验根!
移项,化简得 x=2
引例2:小杰和小莉两人从A地同时出发向相距600米的B地跑去,小杰的速度是小莉的2倍,小杰比小莉早1分半钟到达B地。那么小杰和小莉的速度各是多少?
解分式方程的步骤:
(1)化:去分母,化成整式方程;
(2)解:解整式方程(一元一次方程);
(3)验:检验(可能产生増根).
课堂小结
思考题
则増根是 ,m为 .
有増根,
分式方程
作业布置
练习册P52-53 习题 10.5
课堂小结
分式方程
整式方程
转化
去分母
解
方
程
求整式方程的解
求分式方程的解
检验
