2021年沪教版(上海)中考复习训练(word版含答案)
文档属性
| 名称 | 2021年沪教版(上海)中考复习训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览



文档简介
初三数学复习训练
一、选择题(本大题共6题,每题4分,满分24分)
1.化简的结果是(
)
(A)
(B)
(C)
(D)
2.下列二次根式中,不是最简二次根式的是(
)
(A)
(B)
(C)
(D)
3.若关于的方程有两个不相等的实数根,则的取值范围是(
)
(A)
(B)
(C)
(D)
4.已知第二象限内点P到x轴的距离为2,到y轴的距离为3,则点P的坐标为(
)
(A)
(B)
(C)
(D)
5.顺次联结等腰梯形四边中点所得的四边形是(
)
(A)等腰梯形
(B)矩形
(C)菱形
(D)正方形
6.下列命题中,正确的是
(
)
(A)Rt△ABC中,CD是AB上中线,则CD=AB;
(B)点P是∠AOB的平分线上一点,点M、N分别在OA、OB上,则PM=PN;
(C)Rt△ABC中,若∠B=30°,则AC=AB;
(D)一边上的中线等于这边的一半的三角形是直角三角形.
二、填空题(本大题共12题,每题4分,满分48分)
7.分解因式:=
.
8.计算:
.
9.方程的解是
.
10.不等式组的解集是
.
11.把二元二次方程转化为两个二元一次方程是
.
12.若一次函数的图像经过第一、二、三象限,则的取值范围是
.
13.抛物线的顶点坐标是
.
14.某单位举行联欢活动,在87张对奖券中,有一等奖一张,二等奖2张,三等奖3张
,则从中任意抽取一张对奖券恰为二等奖的概率是
.(结果用分数表示)
15.为了了解某校九年级学生的身体素质情况,在该校九年级随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出频数分布直方图(如图,每组数据可含最小值,不含最大值),如果在一分钟内跳绳次数少于120次的为不合格,那么可以估计该校九年级300名学生中跳绳不合格的人数为
.
16.梯形ABCD中,AB//CD,E、F是AD、BC的中点,若=,=,那么用、
地线性组合表示向量=
_.
17.已知△ABC中,点G是△ABC的重心,过点G作DE∥BC,与AB相交于点D,与AC相交于点E,如果△ABC的面积为9,那么△ADE的面积是
.
18.已知BC是⊙O的弦,以BC为斜边在⊙O内作等腰直角△ABC,如果BC=6,OA=1,那么⊙O的半径是
.
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
计算:
20.(本题满分10分)
解方程:.
21.(本题满分10分,第(1)题4分,第(2)题6分)
已知:如图,点D、E分别在线段AC、AB上,.
(1)求证:⊿AEC∽⊿ADB;
(2)AB=4,DB=5,sinC=,求.
22.(本题共2小题,第(1)小题5分,第(2)小题5分,满分10分)
某地举办乒乓球比赛,其组织费用y(元)包括两部分:第一部分是租用比赛场地等的固定费用b(元),第二部分是与参赛人数x(人)成正比例的人员费用.已知当x=20时,y=1600,当x=30时,y=2000.
(1)求y与x之间的函数关系式;
(2)如果有50名运动员参加比赛,且全部费用由运动员平均分摊,那么每名运动员将分担到多少元?
23.(本题共2小题,每小题6分,满分12分)
已知:如图,在梯形ABCD中,AD
//
BC,E、F分别为边AB、DC的中点,CG
//
DE,交EF的延长线于点G.
(1)求证:四边形DECG是平行四边形;
(2)当ED平分∠ADC时,求证:四边形DECG是矩形.
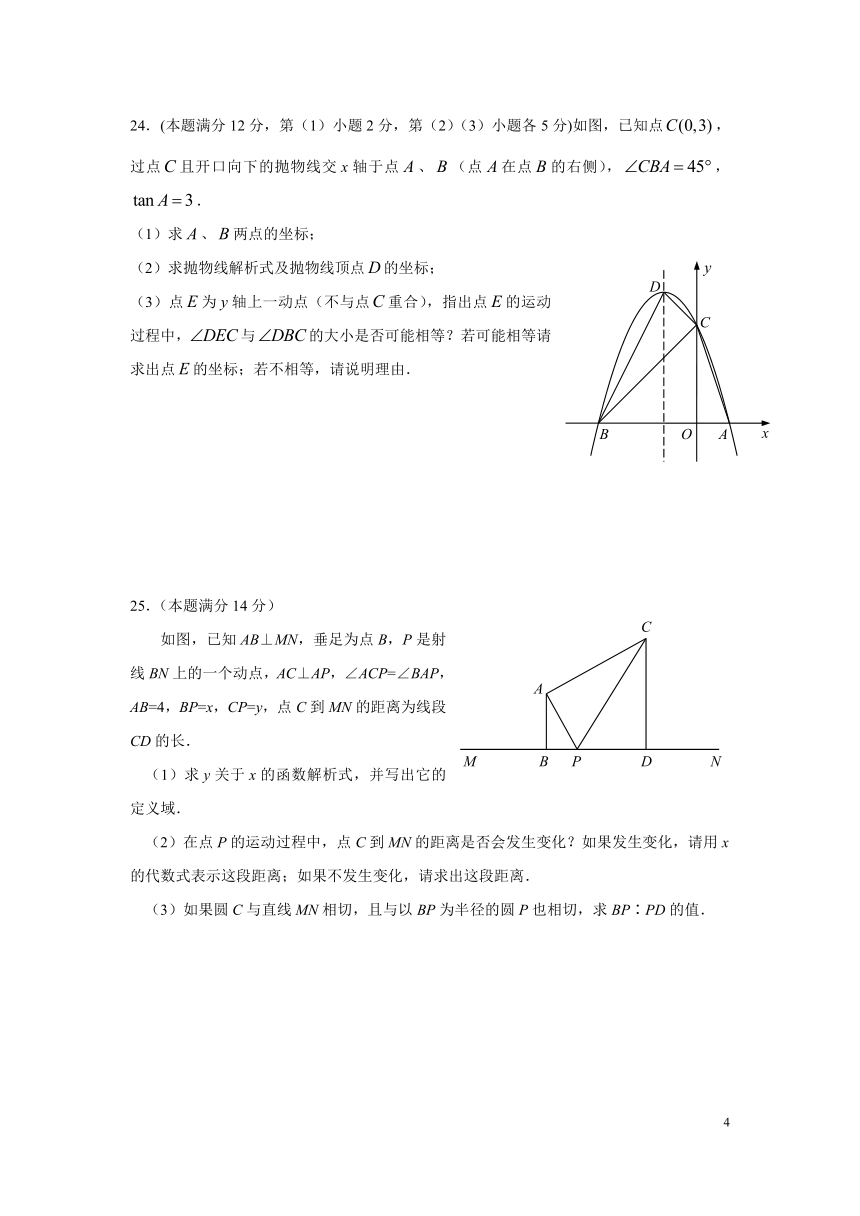
24.(本题满分12分,第(1)小题2分,第(2)(3)小题各5分)如图,已知点,过点且开口向下的抛物线交x轴于点、(点在点的右侧),,.
(1)求、两点的坐标;
(2)求抛物线解析式及抛物线顶点的坐标;
(3)点为y轴上一动点(不与点重合),指出点的运动过程中,与的大小是否可能相等?若可能相等请求出点的坐标;若不相等,请说明理由.
25.(本题满分14分)
如图,已知AB⊥MN,垂足为点B,P是射线BN上的一个动点,AC⊥AP,∠ACP=∠BAP,AB=4,BP=x,CP=y,点C到MN的距离为线段CD的长.
(1)求y关于x的函数解析式,并写出它的定义域.
(2)在点P的运动过程中,点C到MN的距离是否会发生变化?如果发生变化,请用x的代数式表示这段距离;如果不发生变化,请求出这段距离.
(3)如果圆C与直线MN相切,且与以BP为半径的圆P也相切,求BP∶PD的值.
初三数学复习训练参考答案
一.选择题
1.B;
2.D;
3.B;
4.C;
5.C;
6.D;
二、填空题
7.
;
8.
;
9.;
10.;
11.
和;
12.;
13.(0,);14.;
15.72;
16.;
17.4;
18.或5
三.解答题
19.
解:原式=-------------------------(每项化简2分共8分)
------------------------------------------------------------(2分)
20.
去分母得:…………………………………3
分
化简并整理得:
……………………………………………3分
解得:
或者
……………………………………………2分
经检验,是原方程的根,为增根。………………………………1分:
所以,原方程的根为。…………………………………1分:
21.证明:(1)∵
∴
……………………………………(2分)
又∵∠DAB=∠EAC,
∴⊿AEC∽⊿ADB.
……………………………………(2分)
解
(2)∵⊿AEC∽⊿ADB,
∴∠B=∠C.…………………………………………(2分)
过点A作BD的垂线,垂足为F,
则………………………(2分)
∴……………(2分)
22、(1)设…………………………1分
把x=20,y=1600;x=30,y=2000分别代入得:………………………1分
解得:…………………………………2分
∴…………………………1分
(2)把代入解析式得:…………………………………2分
元…………………………………2分
答:每名运动员要支付56元…………………………1分
23.证明:(1)∵
F是边CD的中点,∴
DF
=
CF.…………………………(1分)
∵
CG
//
DE,
∴
∠DEF
=∠CGF.………………………………………………(1分)
又
∠DFE
=∠CFG,
∴
△DEF≌△CGF(A.A.S).………………………………(2分)
∴
DE
=
CG.………………………………………………………(1分)
又
CG
//
DE,
∴
四边形DECG是平行四边形.…………………………………(1分)
(2)∵
ED平分∠ADC,∴
∠ADE
=∠FDE.………………………(1分)
∵
E、F分别为边AB、DC的中点,
∴
EF
//
AD.
∴
∠ADE
=∠DEF.………………………………………………(1分)
∴
∠DEF
=∠EDF.即得
EF
=
DF
=
CF.
∴
∠FEC
=∠ECF.………………………………………………(1分)
即得
∠EDC
+∠DCE
=∠DEC.
∵
∠EDC
+∠DCE
+∠DEC
=
180°,
∴
2∠DEC
=
180°.
即得
∠DEC
=
90°.………………………………………………(2分)
又∵
四边形DECG是平行四边形,
∴
四边形DECG是矩形.…………………………………………(1分)
24、(1)
在
………………………2分
(2)
则,————(2分)
解得:.————(1分)
∴此函数解析式为.————(1分)
.
∴顶点为.————(1分)
(3)在点E的运动过程中,∠DEC与∠DBC的大小可能相等。
………………………2分
,则
当点E在点C上方时,
∴
………………………2分
当点E在点C下方时,
同理可得,当时,
………………………1分
综上所述,在点E的运动过程中,∠DEC与∠DBC的大小可能相等。当时点的坐标为。
25.解:(1)∵AB⊥MN,AC⊥AP,∴.
又∵∠ACP=∠BAP,∴△ABP∽△CAP.……………………………………(1分)
∴,即.………………………………(1分)
∴所求的函数解析式为
.……………………(1分,1分)
(2)CD的长不会发生变化.……………………………………………………(1分)
延长CA交直线MN于点E.………………………………………………(1分)
∵AC⊥AP,∴.
∵∠ACP=∠BAP,∴.∴.
∴.
∴.
………………………………………………………………(1分)
∵,,∴.
∴.…………………………………………………………(1分)
∵AB=4,∴.………………………………………………………(1分)
(3)∵圆C与直线MN相切,∴圆C的半径为8.……………………………(1分)
(i)当圆C与圆P外切时,,即.
∴.∴.
……………………………………………(1分)
∴.
…………………………………………………………(1分)
(ii)当圆C与圆P内切时,,即,
∴.
∴
或
.
∴(不合题意,舍去)或无实数解.……………………(1分,1分)
∴综上所述
.
2
一、选择题(本大题共6题,每题4分,满分24分)
1.化简的结果是(
)
(A)
(B)
(C)
(D)
2.下列二次根式中,不是最简二次根式的是(
)
(A)
(B)
(C)
(D)
3.若关于的方程有两个不相等的实数根,则的取值范围是(
)
(A)
(B)
(C)
(D)
4.已知第二象限内点P到x轴的距离为2,到y轴的距离为3,则点P的坐标为(
)
(A)
(B)
(C)
(D)
5.顺次联结等腰梯形四边中点所得的四边形是(
)
(A)等腰梯形
(B)矩形
(C)菱形
(D)正方形
6.下列命题中,正确的是
(
)
(A)Rt△ABC中,CD是AB上中线,则CD=AB;
(B)点P是∠AOB的平分线上一点,点M、N分别在OA、OB上,则PM=PN;
(C)Rt△ABC中,若∠B=30°,则AC=AB;
(D)一边上的中线等于这边的一半的三角形是直角三角形.
二、填空题(本大题共12题,每题4分,满分48分)
7.分解因式:=
.
8.计算:
.
9.方程的解是
.
10.不等式组的解集是
.
11.把二元二次方程转化为两个二元一次方程是
.
12.若一次函数的图像经过第一、二、三象限,则的取值范围是
.
13.抛物线的顶点坐标是
.
14.某单位举行联欢活动,在87张对奖券中,有一等奖一张,二等奖2张,三等奖3张
,则从中任意抽取一张对奖券恰为二等奖的概率是
.(结果用分数表示)
15.为了了解某校九年级学生的身体素质情况,在该校九年级随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出频数分布直方图(如图,每组数据可含最小值,不含最大值),如果在一分钟内跳绳次数少于120次的为不合格,那么可以估计该校九年级300名学生中跳绳不合格的人数为
.
16.梯形ABCD中,AB//CD,E、F是AD、BC的中点,若=,=,那么用、
地线性组合表示向量=
_.
17.已知△ABC中,点G是△ABC的重心,过点G作DE∥BC,与AB相交于点D,与AC相交于点E,如果△ABC的面积为9,那么△ADE的面积是
.
18.已知BC是⊙O的弦,以BC为斜边在⊙O内作等腰直角△ABC,如果BC=6,OA=1,那么⊙O的半径是
.
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
计算:
20.(本题满分10分)
解方程:.
21.(本题满分10分,第(1)题4分,第(2)题6分)
已知:如图,点D、E分别在线段AC、AB上,.
(1)求证:⊿AEC∽⊿ADB;
(2)AB=4,DB=5,sinC=,求.
22.(本题共2小题,第(1)小题5分,第(2)小题5分,满分10分)
某地举办乒乓球比赛,其组织费用y(元)包括两部分:第一部分是租用比赛场地等的固定费用b(元),第二部分是与参赛人数x(人)成正比例的人员费用.已知当x=20时,y=1600,当x=30时,y=2000.
(1)求y与x之间的函数关系式;
(2)如果有50名运动员参加比赛,且全部费用由运动员平均分摊,那么每名运动员将分担到多少元?
23.(本题共2小题,每小题6分,满分12分)
已知:如图,在梯形ABCD中,AD
//
BC,E、F分别为边AB、DC的中点,CG
//
DE,交EF的延长线于点G.
(1)求证:四边形DECG是平行四边形;
(2)当ED平分∠ADC时,求证:四边形DECG是矩形.
24.(本题满分12分,第(1)小题2分,第(2)(3)小题各5分)如图,已知点,过点且开口向下的抛物线交x轴于点、(点在点的右侧),,.
(1)求、两点的坐标;
(2)求抛物线解析式及抛物线顶点的坐标;
(3)点为y轴上一动点(不与点重合),指出点的运动过程中,与的大小是否可能相等?若可能相等请求出点的坐标;若不相等,请说明理由.
25.(本题满分14分)
如图,已知AB⊥MN,垂足为点B,P是射线BN上的一个动点,AC⊥AP,∠ACP=∠BAP,AB=4,BP=x,CP=y,点C到MN的距离为线段CD的长.
(1)求y关于x的函数解析式,并写出它的定义域.
(2)在点P的运动过程中,点C到MN的距离是否会发生变化?如果发生变化,请用x的代数式表示这段距离;如果不发生变化,请求出这段距离.
(3)如果圆C与直线MN相切,且与以BP为半径的圆P也相切,求BP∶PD的值.
初三数学复习训练参考答案
一.选择题
1.B;
2.D;
3.B;
4.C;
5.C;
6.D;
二、填空题
7.
;
8.
;
9.;
10.;
11.
和;
12.;
13.(0,);14.;
15.72;
16.;
17.4;
18.或5
三.解答题
19.
解:原式=-------------------------(每项化简2分共8分)
------------------------------------------------------------(2分)
20.
去分母得:…………………………………3
分
化简并整理得:
……………………………………………3分
解得:
或者
……………………………………………2分
经检验,是原方程的根,为增根。………………………………1分:
所以,原方程的根为。…………………………………1分:
21.证明:(1)∵
∴
……………………………………(2分)
又∵∠DAB=∠EAC,
∴⊿AEC∽⊿ADB.
……………………………………(2分)
解
(2)∵⊿AEC∽⊿ADB,
∴∠B=∠C.…………………………………………(2分)
过点A作BD的垂线,垂足为F,
则………………………(2分)
∴……………(2分)
22、(1)设…………………………1分
把x=20,y=1600;x=30,y=2000分别代入得:………………………1分
解得:…………………………………2分
∴…………………………1分
(2)把代入解析式得:…………………………………2分
元…………………………………2分
答:每名运动员要支付56元…………………………1分
23.证明:(1)∵
F是边CD的中点,∴
DF
=
CF.…………………………(1分)
∵
CG
//
DE,
∴
∠DEF
=∠CGF.………………………………………………(1分)
又
∠DFE
=∠CFG,
∴
△DEF≌△CGF(A.A.S).………………………………(2分)
∴
DE
=
CG.………………………………………………………(1分)
又
CG
//
DE,
∴
四边形DECG是平行四边形.…………………………………(1分)
(2)∵
ED平分∠ADC,∴
∠ADE
=∠FDE.………………………(1分)
∵
E、F分别为边AB、DC的中点,
∴
EF
//
AD.
∴
∠ADE
=∠DEF.………………………………………………(1分)
∴
∠DEF
=∠EDF.即得
EF
=
DF
=
CF.
∴
∠FEC
=∠ECF.………………………………………………(1分)
即得
∠EDC
+∠DCE
=∠DEC.
∵
∠EDC
+∠DCE
+∠DEC
=
180°,
∴
2∠DEC
=
180°.
即得
∠DEC
=
90°.………………………………………………(2分)
又∵
四边形DECG是平行四边形,
∴
四边形DECG是矩形.…………………………………………(1分)
24、(1)
在
………………………2分
(2)
则,————(2分)
解得:.————(1分)
∴此函数解析式为.————(1分)
.
∴顶点为.————(1分)
(3)在点E的运动过程中,∠DEC与∠DBC的大小可能相等。
………………………2分
,则
当点E在点C上方时,
∴
………………………2分
当点E在点C下方时,
同理可得,当时,
………………………1分
综上所述,在点E的运动过程中,∠DEC与∠DBC的大小可能相等。当时点的坐标为。
25.解:(1)∵AB⊥MN,AC⊥AP,∴.
又∵∠ACP=∠BAP,∴△ABP∽△CAP.……………………………………(1分)
∴,即.………………………………(1分)
∴所求的函数解析式为
.……………………(1分,1分)
(2)CD的长不会发生变化.……………………………………………………(1分)
延长CA交直线MN于点E.………………………………………………(1分)
∵AC⊥AP,∴.
∵∠ACP=∠BAP,∴.∴.
∴.
∴.
………………………………………………………………(1分)
∵,,∴.
∴.…………………………………………………………(1分)
∵AB=4,∴.………………………………………………………(1分)
(3)∵圆C与直线MN相切,∴圆C的半径为8.……………………………(1分)
(i)当圆C与圆P外切时,,即.
∴.∴.
……………………………………………(1分)
∴.
…………………………………………………………(1分)
(ii)当圆C与圆P内切时,,即,
∴.
∴
或
.
∴(不合题意,舍去)或无实数解.……………………(1分,1分)
∴综上所述
.
2
同课章节目录
