2020-2021学年人教A版数学 选修2-2课件:1.1.3 导数的几何意义(共31张PPT)
文档属性
| 名称 | 2020-2021学年人教A版数学 选修2-2课件:1.1.3 导数的几何意义(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
1.1.3 导数的几何意义
1.导数的几何意义
曲线y=f(x)在点(x0,f(x0))处的导数f′(x0)的几何意义为______________,相应地,曲线y=f(x)在点(x0,f(x0))处的切线方程为____________________.
切线的斜率
1.函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
A.在点x0处的斜率
B.在点(x0,f(x0))处的切线与x轴所夹锐角的正切值
C.曲线y=f(x)在点(x0,f(x0))处切线的斜率
D.点(x0,f(x0))与点(0,0)连线的斜率
【答案】C
2.(多选题)曲线y=x2在x=0处的( )
A.切线斜率为0
B.切线方程为y=2x
C.没有切线
D.切线方程为y=0
【答案】AD
3.已知曲线y=x3在点(2,8)处的切线方程为12x-ay-16=0,则实数a的值是( )
A.-1
B.1
C.-2
D.2
【答案】B
4.曲线y=x2+3x在点(2,10)处的切线的斜率是______.
【答案】7
【例1】
求曲线y=x3-2x在点(1,-1)处的切线方程.
【解题探究】根据导数的几何意义求切线的斜率即可.
求曲线在某点处的切线方程
求曲线在某点处的切线,关键是利用导数求出切线斜率.
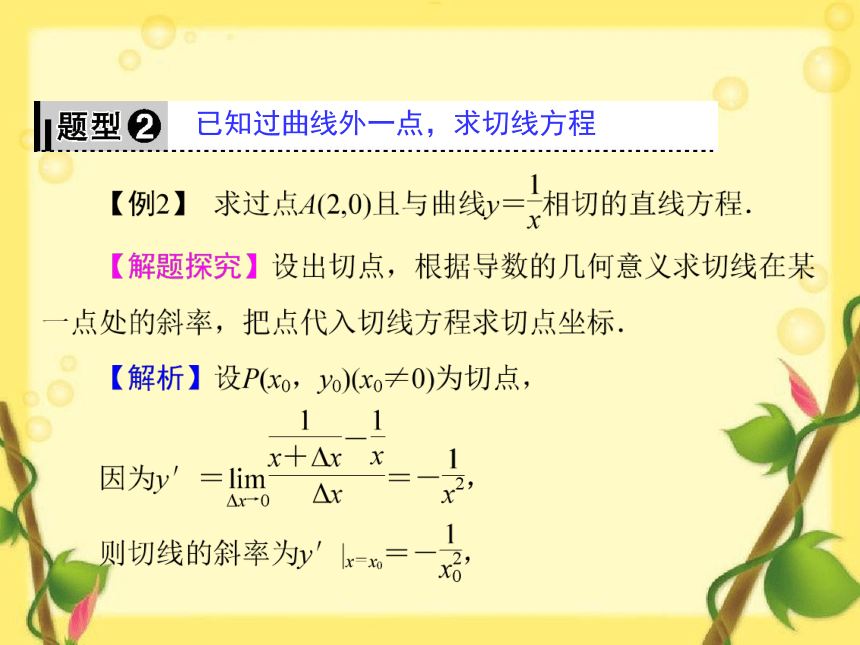
已知过曲线外一点,求切线方程
求过曲线外一点的切线方程时,设切点坐标,求出切线方程,再把已知点代入切线方程求得切点坐标,进而求得切线.也可将切线的斜率用两点式和切点处的导数分别表示出来,求出切点,进而求得切线.
2.试求过点P(3,5)且与曲线y=x2相切的直线方程.
【例3】
已知曲线y=x2在点P处的切线分别满足下列条件,求点P的坐标.
(1)平行于直线y=4x-5;
(2)与x轴成135°的倾斜角.
【解题探究】设切点坐标,根据导数的几何意义求切线斜率,然后利用条件(平行、倾斜角)求切点坐标.
求切点坐标
求切点坐标的步骤
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
3.已知曲线C:y=x3-3x2+2x,直线l:y=kx且直线l与曲线C相切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标.
忽略隐含条件致误
【示例】
已知曲线y=ax2+bx-5在点(2,1)处的切线方程为y=-3x+7,求a,b的值.
【错因分析】忽视了切点在曲线上这一条件而导致思路受阻.
3.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在切线上,则设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
1.曲线f(x)=x2+3x在点A(1,4)处的切线斜率为( )
A.2
B.5
C.6
D.11
【答案】B
4.(2017年安徽马鞍山期中)如图函数f(x)的图象在点P处的切线为y=-2x+5,则f(2)+f′(2)=________.
【答案】-1
1.1.3 导数的几何意义
1.导数的几何意义
曲线y=f(x)在点(x0,f(x0))处的导数f′(x0)的几何意义为______________,相应地,曲线y=f(x)在点(x0,f(x0))处的切线方程为____________________.
切线的斜率
1.函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
A.在点x0处的斜率
B.在点(x0,f(x0))处的切线与x轴所夹锐角的正切值
C.曲线y=f(x)在点(x0,f(x0))处切线的斜率
D.点(x0,f(x0))与点(0,0)连线的斜率
【答案】C
2.(多选题)曲线y=x2在x=0处的( )
A.切线斜率为0
B.切线方程为y=2x
C.没有切线
D.切线方程为y=0
【答案】AD
3.已知曲线y=x3在点(2,8)处的切线方程为12x-ay-16=0,则实数a的值是( )
A.-1
B.1
C.-2
D.2
【答案】B
4.曲线y=x2+3x在点(2,10)处的切线的斜率是______.
【答案】7
【例1】
求曲线y=x3-2x在点(1,-1)处的切线方程.
【解题探究】根据导数的几何意义求切线的斜率即可.
求曲线在某点处的切线方程
求曲线在某点处的切线,关键是利用导数求出切线斜率.
已知过曲线外一点,求切线方程
求过曲线外一点的切线方程时,设切点坐标,求出切线方程,再把已知点代入切线方程求得切点坐标,进而求得切线.也可将切线的斜率用两点式和切点处的导数分别表示出来,求出切点,进而求得切线.
2.试求过点P(3,5)且与曲线y=x2相切的直线方程.
【例3】
已知曲线y=x2在点P处的切线分别满足下列条件,求点P的坐标.
(1)平行于直线y=4x-5;
(2)与x轴成135°的倾斜角.
【解题探究】设切点坐标,根据导数的几何意义求切线斜率,然后利用条件(平行、倾斜角)求切点坐标.
求切点坐标
求切点坐标的步骤
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
3.已知曲线C:y=x3-3x2+2x,直线l:y=kx且直线l与曲线C相切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标.
忽略隐含条件致误
【示例】
已知曲线y=ax2+bx-5在点(2,1)处的切线方程为y=-3x+7,求a,b的值.
【错因分析】忽视了切点在曲线上这一条件而导致思路受阻.
3.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在切线上,则设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
1.曲线f(x)=x2+3x在点A(1,4)处的切线斜率为( )
A.2
B.5
C.6
D.11
【答案】B
4.(2017年安徽马鞍山期中)如图函数f(x)的图象在点P处的切线为y=-2x+5,则f(2)+f′(2)=________.
【答案】-1
