人教版数学七年级下册:第五章 相交线与平行线 5.1—5.2平行线及其判定 阶段练习(word附答案)
文档属性
| 名称 | 人教版数学七年级下册:第五章 相交线与平行线 5.1—5.2平行线及其判定 阶段练习(word附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 130.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览


文档简介
相交线与平行线 阶段练习(5.1—5.2)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.邻补角是指( )
A.和为180°的两个角
B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.下列各图中,∠1与∠2是对顶角的是( )
3.如图,直线AB,CD被EF所截,下列说法正确的有( )
①∠3与∠5是内错角;②∠2与∠7是同位角;③∠4与∠5是同旁内角;④图中有4对同位角,2对内错角,2对同旁内角;⑤∠1与∠7是内错角.
A.1个 B.2个 C.3个 D.4个
4.下列说法错误的是( )
A.两条直线相交,有一个角是直角,则两条直线互相垂直
B.若互为对顶角的两角之和为180°,则两直线互相垂直
C.两直线相交,所构成的四个角中,若有两个角相等,则两直线互相垂直
D.在同一平面上,过点A作直线l的垂线,这样的垂线只有一条
5.如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是(A)
A.20° B.30° C.40° D.50°
6.下列说法错误的是( )
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,则它和另一条也相交
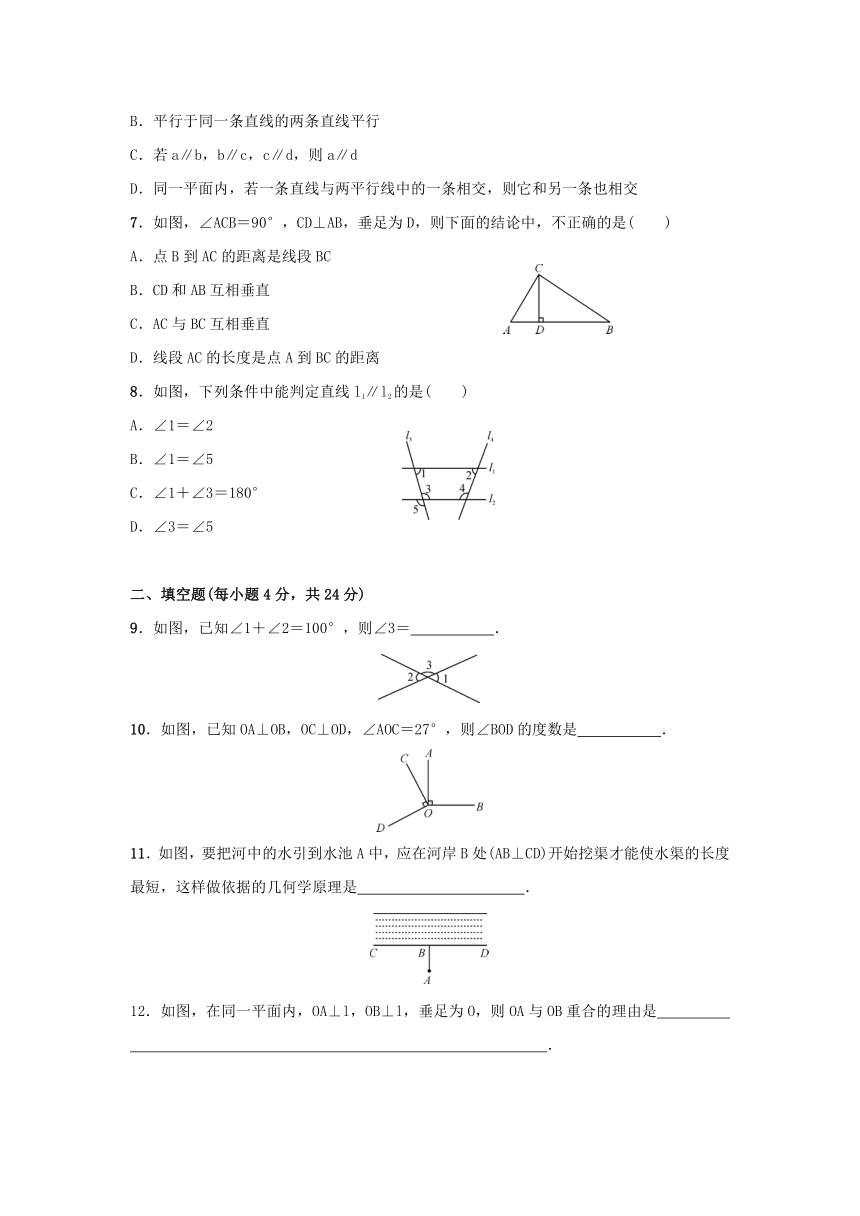
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是( )
3285490220980A.点B到AC的距离是线段BC
B.CD和AB互相垂直
C.AC与BC互相垂直
D.线段AC的长度是点A到BC的距离
8.如图,下列条件中能判定直线l1∥l2的是( )
2393950205740A.∠1=∠2
B.∠1=∠5
C.∠1+∠3=180°
D.∠3=∠5
二、填空题(每小题4分,共24分)
9.如图,已知∠1+∠2=100°,则∠3= .
10.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是 .
11.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 .
如图,在同一平面内,OA⊥l,OB⊥l,垂足为O,则OA与OB重合的理由是
.
13.如图所示,AB与BC被AD所截得的内错角是 ;DE与AC被直线AD所截得的内错角是 ;图中∠4的内错角是 .
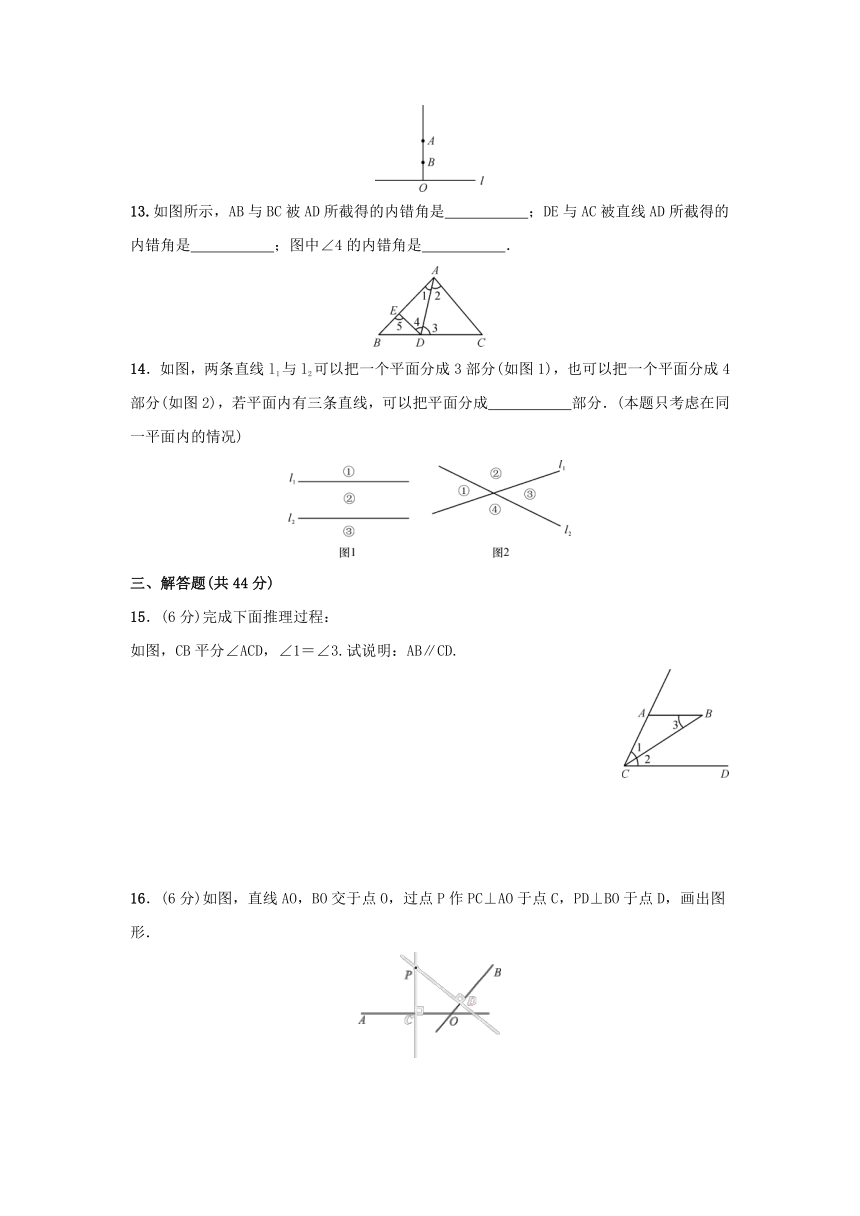
14.如图,两条直线l1与l2可以把一个平面分成3部分(如图1),也可以把一个平面分成4部分(如图2),若平面内有三条直线,可以把平面分成 部分.(本题只考虑在同一平面内的情况)
三、解答题(共44分)
15.(6分)完成下面推理过程:
如图,CB平分∠ACD,∠1=∠3.试说明:AB∥CD.
16.(6分)如图,直线AO,BO交于点O,过点P作PC⊥AO于点C,PD⊥BO于点D,画出图形.
17.(6分)如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明:AB∥CD.
18.(8分)如图,已知直线l1,l2,l3被直线l所截,∠α=105°,∠β=75°,∠γ=75°,运用已知条件,你能找出哪两条直线是平行的吗?若能,请写出理由.
19.(8分)如图,AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.
20.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示是光线从空气射入水中,再从水中射入空气的示意图.由于折射率相同,已知∠1=∠4,∠2=∠3,请你用所学知识来判断光线c与光线d是否平行?并说明理由.
参考答案:
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.邻补角是指( D )
A.和为180°的两个角
B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.下列各图中,∠1与∠2是对顶角的是(C)
3.如图,直线AB,CD被EF所截,下列说法正确的有(C)
①∠3与∠5是内错角;②∠2与∠7是同位角;③∠4与∠5是同旁内角;④图中有4对同位角,2对内错角,2对同旁内角;⑤∠1与∠7是内错角.
A.1个 B.2个 C.3个 D.4个
4.下列说法错误的是(C)
A.两条直线相交,有一个角是直角,则两条直线互相垂直
B.若互为对顶角的两角之和为180°,则两直线互相垂直
C.两直线相交,所构成的四个角中,若有两个角相等,则两直线互相垂直
D.在同一平面上,过点A作直线l的垂线,这样的垂线只有一条
5.如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是(A)
A.20° B.30° C.40° D.50°
6.下列说法错误的是(A)
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,则它和另一条也相交
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是(A)
A.点B到AC的距离是线段BC
B.CD和AB互相垂直
C.AC与BC互相垂直
D.线段AC的长度是点A到BC的距离
8.如图,下列条件中能判定直线l1∥l2的是(C)
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
二、填空题(每小题4分,共24分)
9.如图,已知∠1+∠2=100°,则∠3=130°.
10.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是153°.
11.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.
12.如图,在同一平面内,OA⊥l,OB⊥l,垂足为O,则OA与OB重合的理由是同一平面内,过一点有且只有一条直线与已知直线垂直.
13.如图所示,AB与BC被AD所截得的内错角是∠1和∠3;DE与AC被直线AD所截得的内错角是∠2和∠4;图中∠4的内错角是∠5和∠2.
14.如图,两条直线l1与l2可以把一个平面分成3部分(如图1),也可以把一个平面分成4部分(如图2),若平面内有三条直线,可以把平面分成4或6或7部分.(本题只考虑在同一平面内的情况)
三、解答题(共44分)
15.(6分)完成下面推理过程:
如图,CB平分∠ACD,∠1=∠3.试说明:AB∥CD.
解:∵CB平分∠ACD,
∴∠1=∠2(角平分线的定义).
∵∠1=∠3,
∴∠2=∠3.
∴AB∥CD(内错角相等,两直线平行).
16.(6分)如图,直线AO,BO交于点O,过点P作PC⊥AO于点C,PD⊥BO于点D,画出图形.
解:如图,作∠ACP=90°,作∠PDB=90°,则直线PC,PD即为所求.
17.(6分)如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明:AB∥CD.
解:∵OF平分∠EOD,∠FOD=25°,
∴∠EOD=2∠FOD=50°.
又∵∠OEB=130°,
∴∠OEB+∠EOD=180°.
∴AB∥CD(同旁内角互补,两直线平行).
18.(8分)如图,已知直线l1,l2,l3被直线l所截,∠α=105°,∠β=75°,∠γ=75°,运用已知条件,你能找出哪两条直线是平行的吗?若能,请写出理由.
解:l1∥l2∥l3.理由:
∵∠1=∠β=75°,∠α=105°,
∴∠α+∠1=180°.
∴l1∥l2(同旁内角互补,两直线平行).
∵∠β=75°,∠γ=75°,
∴∠β=∠γ.
∴l2∥l3(内错角相等,两直线平行).
∴l1∥l2∥l3(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
19.(8分)如图,AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.
解:∵AB,CD相交于点O,
∴∠BOD=∠AOC=40°.
∵OD平分∠BOF,
∴∠DOF=∠BOD=40°.
∵OE⊥CD,
∴∠EOD=90°.
∴∠EOF=∠EOD+∠DOF=130°.
20.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示是光线从空气射入水中,再从水中射入空气的示意图.由于折射率相同,已知∠1=∠4,∠2=∠3,请你用所学知识来判断光线c与光线d是否平行?并说明理由.
解:c∥d.理由如下:
∵∠1+∠5=180°,∠4+∠6=180°,∠1=∠4,
∴∠5=∠6.
∵∠2=∠3,
∴∠2+∠5=∠3+∠6.
∴c∥d.
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.邻补角是指( )
A.和为180°的两个角
B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.下列各图中,∠1与∠2是对顶角的是( )
3.如图,直线AB,CD被EF所截,下列说法正确的有( )
①∠3与∠5是内错角;②∠2与∠7是同位角;③∠4与∠5是同旁内角;④图中有4对同位角,2对内错角,2对同旁内角;⑤∠1与∠7是内错角.
A.1个 B.2个 C.3个 D.4个
4.下列说法错误的是( )
A.两条直线相交,有一个角是直角,则两条直线互相垂直
B.若互为对顶角的两角之和为180°,则两直线互相垂直
C.两直线相交,所构成的四个角中,若有两个角相等,则两直线互相垂直
D.在同一平面上,过点A作直线l的垂线,这样的垂线只有一条
5.如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是(A)
A.20° B.30° C.40° D.50°
6.下列说法错误的是( )
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,则它和另一条也相交
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是( )
3285490220980A.点B到AC的距离是线段BC
B.CD和AB互相垂直
C.AC与BC互相垂直
D.线段AC的长度是点A到BC的距离
8.如图,下列条件中能判定直线l1∥l2的是( )
2393950205740A.∠1=∠2
B.∠1=∠5
C.∠1+∠3=180°
D.∠3=∠5
二、填空题(每小题4分,共24分)
9.如图,已知∠1+∠2=100°,则∠3= .
10.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是 .
11.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 .
如图,在同一平面内,OA⊥l,OB⊥l,垂足为O,则OA与OB重合的理由是
.
13.如图所示,AB与BC被AD所截得的内错角是 ;DE与AC被直线AD所截得的内错角是 ;图中∠4的内错角是 .
14.如图,两条直线l1与l2可以把一个平面分成3部分(如图1),也可以把一个平面分成4部分(如图2),若平面内有三条直线,可以把平面分成 部分.(本题只考虑在同一平面内的情况)
三、解答题(共44分)
15.(6分)完成下面推理过程:
如图,CB平分∠ACD,∠1=∠3.试说明:AB∥CD.
16.(6分)如图,直线AO,BO交于点O,过点P作PC⊥AO于点C,PD⊥BO于点D,画出图形.
17.(6分)如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明:AB∥CD.
18.(8分)如图,已知直线l1,l2,l3被直线l所截,∠α=105°,∠β=75°,∠γ=75°,运用已知条件,你能找出哪两条直线是平行的吗?若能,请写出理由.
19.(8分)如图,AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.
20.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示是光线从空气射入水中,再从水中射入空气的示意图.由于折射率相同,已知∠1=∠4,∠2=∠3,请你用所学知识来判断光线c与光线d是否平行?并说明理由.
参考答案:
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.邻补角是指( D )
A.和为180°的两个角
B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.下列各图中,∠1与∠2是对顶角的是(C)
3.如图,直线AB,CD被EF所截,下列说法正确的有(C)
①∠3与∠5是内错角;②∠2与∠7是同位角;③∠4与∠5是同旁内角;④图中有4对同位角,2对内错角,2对同旁内角;⑤∠1与∠7是内错角.
A.1个 B.2个 C.3个 D.4个
4.下列说法错误的是(C)
A.两条直线相交,有一个角是直角,则两条直线互相垂直
B.若互为对顶角的两角之和为180°,则两直线互相垂直
C.两直线相交,所构成的四个角中,若有两个角相等,则两直线互相垂直
D.在同一平面上,过点A作直线l的垂线,这样的垂线只有一条
5.如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是(A)
A.20° B.30° C.40° D.50°
6.下列说法错误的是(A)
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,则它和另一条也相交
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是(A)
A.点B到AC的距离是线段BC
B.CD和AB互相垂直
C.AC与BC互相垂直
D.线段AC的长度是点A到BC的距离
8.如图,下列条件中能判定直线l1∥l2的是(C)
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
二、填空题(每小题4分,共24分)
9.如图,已知∠1+∠2=100°,则∠3=130°.
10.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是153°.
11.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.
12.如图,在同一平面内,OA⊥l,OB⊥l,垂足为O,则OA与OB重合的理由是同一平面内,过一点有且只有一条直线与已知直线垂直.
13.如图所示,AB与BC被AD所截得的内错角是∠1和∠3;DE与AC被直线AD所截得的内错角是∠2和∠4;图中∠4的内错角是∠5和∠2.
14.如图,两条直线l1与l2可以把一个平面分成3部分(如图1),也可以把一个平面分成4部分(如图2),若平面内有三条直线,可以把平面分成4或6或7部分.(本题只考虑在同一平面内的情况)
三、解答题(共44分)
15.(6分)完成下面推理过程:
如图,CB平分∠ACD,∠1=∠3.试说明:AB∥CD.
解:∵CB平分∠ACD,
∴∠1=∠2(角平分线的定义).
∵∠1=∠3,
∴∠2=∠3.
∴AB∥CD(内错角相等,两直线平行).
16.(6分)如图,直线AO,BO交于点O,过点P作PC⊥AO于点C,PD⊥BO于点D,画出图形.
解:如图,作∠ACP=90°,作∠PDB=90°,则直线PC,PD即为所求.
17.(6分)如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明:AB∥CD.
解:∵OF平分∠EOD,∠FOD=25°,
∴∠EOD=2∠FOD=50°.
又∵∠OEB=130°,
∴∠OEB+∠EOD=180°.
∴AB∥CD(同旁内角互补,两直线平行).
18.(8分)如图,已知直线l1,l2,l3被直线l所截,∠α=105°,∠β=75°,∠γ=75°,运用已知条件,你能找出哪两条直线是平行的吗?若能,请写出理由.
解:l1∥l2∥l3.理由:
∵∠1=∠β=75°,∠α=105°,
∴∠α+∠1=180°.
∴l1∥l2(同旁内角互补,两直线平行).
∵∠β=75°,∠γ=75°,
∴∠β=∠γ.
∴l2∥l3(内错角相等,两直线平行).
∴l1∥l2∥l3(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
19.(8分)如图,AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.
解:∵AB,CD相交于点O,
∴∠BOD=∠AOC=40°.
∵OD平分∠BOF,
∴∠DOF=∠BOD=40°.
∵OE⊥CD,
∴∠EOD=90°.
∴∠EOF=∠EOD+∠DOF=130°.
20.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示是光线从空气射入水中,再从水中射入空气的示意图.由于折射率相同,已知∠1=∠4,∠2=∠3,请你用所学知识来判断光线c与光线d是否平行?并说明理由.
解:c∥d.理由如下:
∵∠1+∠5=180°,∠4+∠6=180°,∠1=∠4,
∴∠5=∠6.
∵∠2=∠3,
∴∠2+∠5=∠3+∠6.
∴c∥d.
