人教版数学 七年级下册 5.2.2 平行线的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版数学 七年级下册 5.2.2 平行线的判定 同步练习(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 75.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览



文档简介
5.2.2 平行线的判定
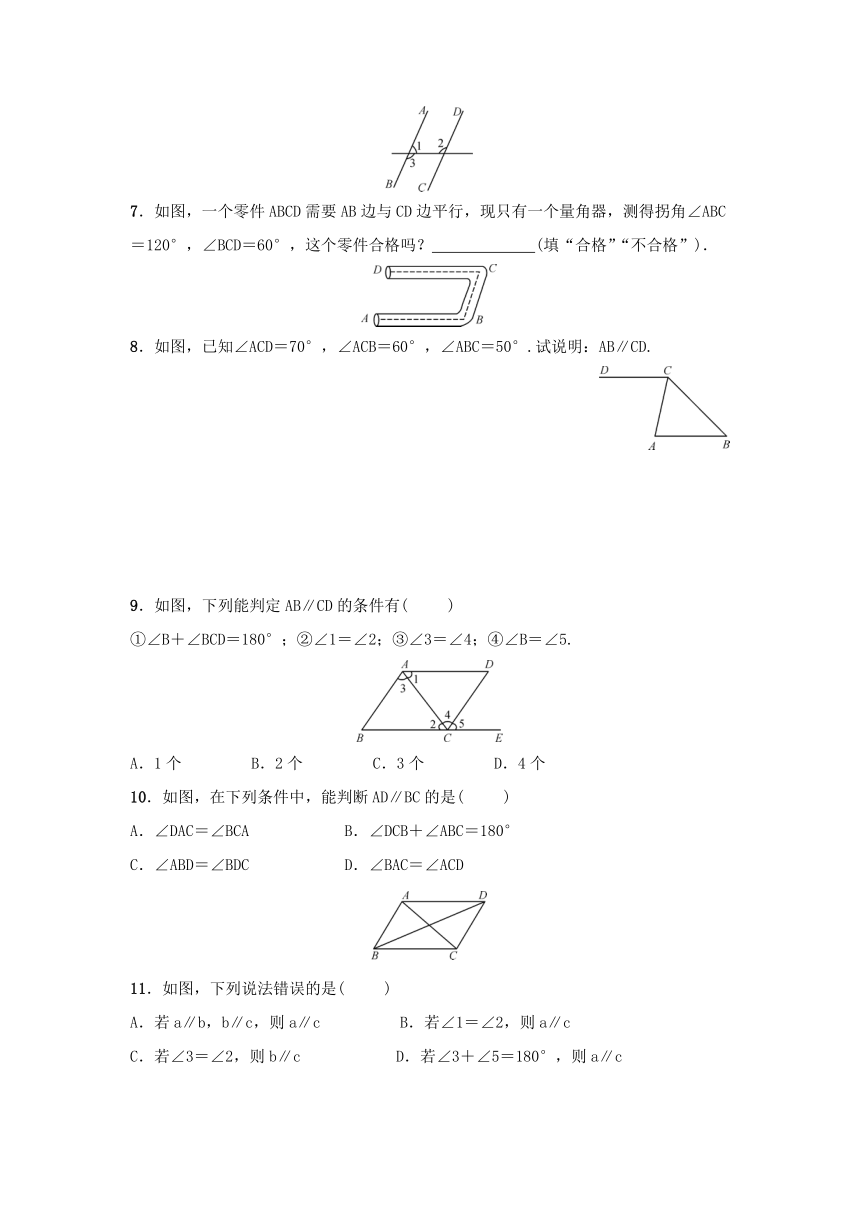
1.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
2.如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
3.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有 .
4.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠A=∠ABE
5.如图,请在括号内填上正确的理由:
∵∠DAC=∠C(已知),
∴AD∥BC( ).
6.如图,已知∠1=70°,要使AB∥CD,则须具备的另一个条件是( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
7.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗? (填“合格”“不合格”).
8.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
9.如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
10.如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
11.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
12.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
13.如图,已知AB⊥BC,BC⊥CD,∠1=∠2,试判断BE与CF的位置关系,并说明你的理由.
14.如图,AB⊥AC,∠1与∠B互余.
(1)AD与BC平行吗?为什么?
(2)若∠B=∠D,则AB与CD平行吗?为什么?
15.已知,如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由.
16.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
参考答案:
1.如图,∠1=120°,要使a∥b,则∠2的大小是(D)
A.60° B.80° C.100° D.120°
2.如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是同位角相等,两直线平行.
3.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有AB∥CD,EF∥CG.
4.如图,能判定EB∥AC的条件是(D)
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠A=∠ABE
5.如图,请在括号内填上正确的理由:
∵∠DAC=∠C(已知),
∴AD∥BC(内错角相等,两直线平行).
6.如图,已知∠1=70°,要使AB∥CD,则须具备的另一个条件是(C)
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
7.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?合格(填“合格”“不合格”).
8.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
解:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=130°.
∵∠ABC=50°,
∴∠BCD+∠ABC=180°.
∴AB∥CD.
9.如图,下列能判定AB∥CD的条件有(C)
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
10.如图,在下列条件中,能判断AD∥BC的是(A)
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
11.如图,下列说法错误的是(C)
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
12.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(任意添加一个符合题意的条件即可)
13.如图,已知AB⊥BC,BC⊥CD,∠1=∠2,试判断BE与CF的位置关系,并说明你的理由.
解:BE∥CF.
理由:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°(垂直的定义).
∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2,
即∠EBC=∠BCF.
∴BE∥CF(内错角相等,两直线平行).
14.如图,AB⊥AC,∠1与∠B互余.
(1)AD与BC平行吗?为什么?
(2)若∠B=∠D,则AB与CD平行吗?为什么?
解:(1)AD∥BC.理由如下:∵AB⊥AC,
∴∠BAC=90°.
∵∠1与∠B互余,
∴∠1+∠B=90°.
∴∠1+∠BAC+∠B=180°,
即∠B+∠BAD=180°.
∴AD∥BC.
(2)AB∥CD.理由如下:
由(1)可知∠B+∠BAD=180°.
∵∠B=∠D,
∴∠D+∠BAD=180°.
∴AB∥CD.
15.已知,如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由.
解:CF∥BD.
方法一:∵BD⊥BE,
∴∠DBE=90°.
∴∠1+∠2=90°.
∵∠1+∠C=90°,∴∠2=∠C.
∴CF∥BD(同位角相等,两直线平行).
方法二:∵BD⊥BE,∴∠DBE=90°.
∵∠1+∠C=90°,
∴∠C+∠DBC=∠1+∠DBE+∠C=90°+90°=180°.
∴CF∥BD(同旁内角互补,两直线平行).
16.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
解:CD∥EF.
理由如下:
∵AB⊥BD,CD⊥BD,
∴∠B+∠D=90°+90°=180°.
∴AB∥CD.
∵∠1+∠2=180°,
∴AB∥EF(同旁内角互补,两直线平行).
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
1.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
2.如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
3.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有 .
4.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠A=∠ABE
5.如图,请在括号内填上正确的理由:
∵∠DAC=∠C(已知),
∴AD∥BC( ).
6.如图,已知∠1=70°,要使AB∥CD,则须具备的另一个条件是( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
7.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗? (填“合格”“不合格”).
8.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
9.如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
10.如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
11.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
12.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
13.如图,已知AB⊥BC,BC⊥CD,∠1=∠2,试判断BE与CF的位置关系,并说明你的理由.
14.如图,AB⊥AC,∠1与∠B互余.
(1)AD与BC平行吗?为什么?
(2)若∠B=∠D,则AB与CD平行吗?为什么?
15.已知,如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由.
16.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
参考答案:
1.如图,∠1=120°,要使a∥b,则∠2的大小是(D)
A.60° B.80° C.100° D.120°
2.如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是同位角相等,两直线平行.
3.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有AB∥CD,EF∥CG.
4.如图,能判定EB∥AC的条件是(D)
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠A=∠ABE
5.如图,请在括号内填上正确的理由:
∵∠DAC=∠C(已知),
∴AD∥BC(内错角相等,两直线平行).
6.如图,已知∠1=70°,要使AB∥CD,则须具备的另一个条件是(C)
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
7.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?合格(填“合格”“不合格”).
8.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
解:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=130°.
∵∠ABC=50°,
∴∠BCD+∠ABC=180°.
∴AB∥CD.
9.如图,下列能判定AB∥CD的条件有(C)
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
10.如图,在下列条件中,能判断AD∥BC的是(A)
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
11.如图,下列说法错误的是(C)
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
12.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(任意添加一个符合题意的条件即可)
13.如图,已知AB⊥BC,BC⊥CD,∠1=∠2,试判断BE与CF的位置关系,并说明你的理由.
解:BE∥CF.
理由:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°(垂直的定义).
∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2,
即∠EBC=∠BCF.
∴BE∥CF(内错角相等,两直线平行).
14.如图,AB⊥AC,∠1与∠B互余.
(1)AD与BC平行吗?为什么?
(2)若∠B=∠D,则AB与CD平行吗?为什么?
解:(1)AD∥BC.理由如下:∵AB⊥AC,
∴∠BAC=90°.
∵∠1与∠B互余,
∴∠1+∠B=90°.
∴∠1+∠BAC+∠B=180°,
即∠B+∠BAD=180°.
∴AD∥BC.
(2)AB∥CD.理由如下:
由(1)可知∠B+∠BAD=180°.
∵∠B=∠D,
∴∠D+∠BAD=180°.
∴AB∥CD.
15.已知,如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由.
解:CF∥BD.
方法一:∵BD⊥BE,
∴∠DBE=90°.
∴∠1+∠2=90°.
∵∠1+∠C=90°,∴∠2=∠C.
∴CF∥BD(同位角相等,两直线平行).
方法二:∵BD⊥BE,∴∠DBE=90°.
∵∠1+∠C=90°,
∴∠C+∠DBC=∠1+∠DBE+∠C=90°+90°=180°.
∴CF∥BD(同旁内角互补,两直线平行).
16.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
解:CD∥EF.
理由如下:
∵AB⊥BD,CD⊥BD,
∴∠B+∠D=90°+90°=180°.
∴AB∥CD.
∵∠1+∠2=180°,
∴AB∥EF(同旁内角互补,两直线平行).
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
