苏教版六年级数学下册4比例的基本性质课件(共17张PPT)
文档属性
| 名称 | 苏教版六年级数学下册4比例的基本性质课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览






文档简介
第四单元 比 例
1、什么叫做比例?
2、什么样的两个比才能组成比例?
表示两个比相等的式子叫做比例。
两个比的比值相等。
复习回顾
应用比例的意义判断下面的比,哪些能组成比例?把组成的比例写出来。
1
3
:
1
4
1 : 5 和 0.8 : 4 12 : 9 和
7 : 4 和 5 : 3 80 : 2 和 200 : 5
1 : 5 =0.8 : 4
内项
12 : 9 =
1
3
:
1
4
80 :2 = 200: 5
外项
3
5
6
10
=
外项
内项
外项
内项
内项
外项
自主探究
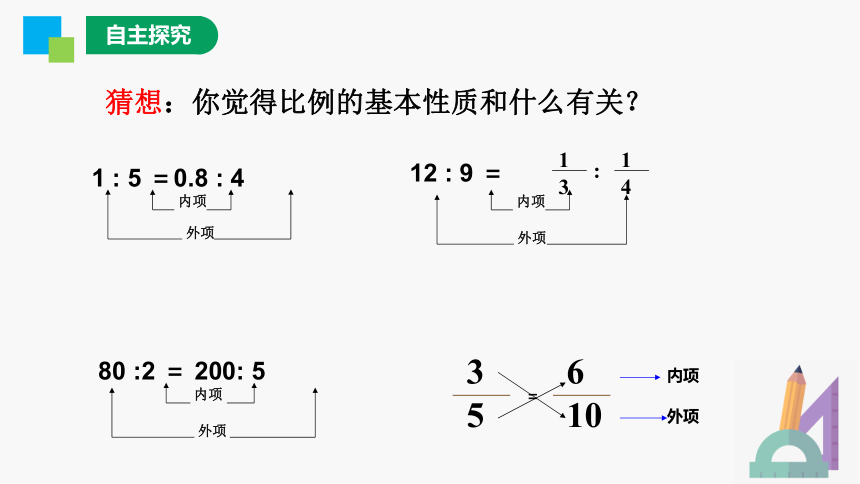
猜想:你觉得比例的基本性质和什么有关?
在比例里,两个外项的积等于两个内项的积?
验证:
这个结论是否正确呢?请再举几个例子,在小组内交流一下。
3 :2=5 :4
在比例里,两个外项的积等于两个内项的积。
如果用字母表示比例的四个项,即a:b=c:d,那么这个规律可以表示为( )
ad = bc
这就是比例的基本性质。
1 : 5 和 0.8 : 4
外项
内项
两个外项的积:1×4=4
两个内项的积: 5×0.8=4
因为乘积相等,所以这两个比可以组成比例。
步骤:
1、假设这两个比可以组成比例。
2、分别找出外项与内项,并计算它们的乘积。
3、根据比例的基本性质判断。
1 : 5 = 0.8 : 4
即1×4= 5×0.8
应用比例的基本性质判断两个比是不是可以组成比例。
1 : 5 和 0.8 : 4
外项
内项
两个外项的积:1×4=4
两个内项的积: 5×0.8=4
因为乘积相等,所以这两个比可以组成比例。
步骤:
1、假设这两个比可以组成比例。
2、分别找出外项与内项,并计算它们的乘积。
3、根据比例的基本性质判断。
1 : 5 = 0.8 : 4
即1×4= 5×0.8
基础练习
练一练:应用比例的基本性质判断下面哪些组的两个比可以组成比例?
(1)10:12和25:30 (2)0.2:0.25和4:50
(3) (4)
2
8
3
27
和
变式练习
第一关:1.5 : 3=( ): 4
想:说说你是怎样想的?
变式练习
第二关:12: ( ) =( ) : 5
还可能是什么答案?这样的答案有多少个呢?
第三关:
a×4=b×3,则 a : b=( ) : ( )
变式练习
拓展练习
根据2×9=3×6,你能用这四个数字写出比例式吗?看谁写的多。
2: ( ) =( ) : 9
2: ( ) =( ) : 9
9: ( ) =( ) : 2
9: ( ) =( ) : 2
3: ( 2 ) =( 9 ) : 6
3: ( 9 ) =( 2 ) : 6
6: ( 2 ) =( 9 ) : 3
6: ( 9 ) =( 2 ) : 3
3
3
3
3
6
6
6
6
判断3、5、8、4这四个数字能不能组成比例?如果不能,如果换一个数字,你可以换成什么数,就能够让它们可以组成例了?
拓展练习
总结回顾
通过本节课的学习,你有什么收获?和大家分享一下?
观察
-猜想
-验证
-归纳
-应用
怎么知道什么!
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
作业布置
课本P41页练习七第1、2、3题。
1、什么叫做比例?
2、什么样的两个比才能组成比例?
表示两个比相等的式子叫做比例。
两个比的比值相等。
复习回顾
应用比例的意义判断下面的比,哪些能组成比例?把组成的比例写出来。
1
3
:
1
4
1 : 5 和 0.8 : 4 12 : 9 和
7 : 4 和 5 : 3 80 : 2 和 200 : 5
1 : 5 =0.8 : 4
内项
12 : 9 =
1
3
:
1
4
80 :2 = 200: 5
外项
3
5
6
10
=
外项
内项
外项
内项
内项
外项
自主探究
猜想:你觉得比例的基本性质和什么有关?
在比例里,两个外项的积等于两个内项的积?
验证:
这个结论是否正确呢?请再举几个例子,在小组内交流一下。
3 :2=5 :4
在比例里,两个外项的积等于两个内项的积。
如果用字母表示比例的四个项,即a:b=c:d,那么这个规律可以表示为( )
ad = bc
这就是比例的基本性质。
1 : 5 和 0.8 : 4
外项
内项
两个外项的积:1×4=4
两个内项的积: 5×0.8=4
因为乘积相等,所以这两个比可以组成比例。
步骤:
1、假设这两个比可以组成比例。
2、分别找出外项与内项,并计算它们的乘积。
3、根据比例的基本性质判断。
1 : 5 = 0.8 : 4
即1×4= 5×0.8
应用比例的基本性质判断两个比是不是可以组成比例。
1 : 5 和 0.8 : 4
外项
内项
两个外项的积:1×4=4
两个内项的积: 5×0.8=4
因为乘积相等,所以这两个比可以组成比例。
步骤:
1、假设这两个比可以组成比例。
2、分别找出外项与内项,并计算它们的乘积。
3、根据比例的基本性质判断。
1 : 5 = 0.8 : 4
即1×4= 5×0.8
基础练习
练一练:应用比例的基本性质判断下面哪些组的两个比可以组成比例?
(1)10:12和25:30 (2)0.2:0.25和4:50
(3) (4)
2
8
3
27
和
变式练习
第一关:1.5 : 3=( ): 4
想:说说你是怎样想的?
变式练习
第二关:12: ( ) =( ) : 5
还可能是什么答案?这样的答案有多少个呢?
第三关:
a×4=b×3,则 a : b=( ) : ( )
变式练习
拓展练习
根据2×9=3×6,你能用这四个数字写出比例式吗?看谁写的多。
2: ( ) =( ) : 9
2: ( ) =( ) : 9
9: ( ) =( ) : 2
9: ( ) =( ) : 2
3: ( 2 ) =( 9 ) : 6
3: ( 9 ) =( 2 ) : 6
6: ( 2 ) =( 9 ) : 3
6: ( 9 ) =( 2 ) : 3
3
3
3
3
6
6
6
6
判断3、5、8、4这四个数字能不能组成比例?如果不能,如果换一个数字,你可以换成什么数,就能够让它们可以组成例了?
拓展练习
总结回顾
通过本节课的学习,你有什么收获?和大家分享一下?
观察
-猜想
-验证
-归纳
-应用
怎么知道什么!
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
作业布置
课本P41页练习七第1、2、3题。
