浙江省绍兴市上虞区2021届高三上学期期末教学质量调测数学试题 Word版含答案
文档属性
| 名称 | 浙江省绍兴市上虞区2021届高三上学期期末教学质量调测数学试题 Word版含答案 | 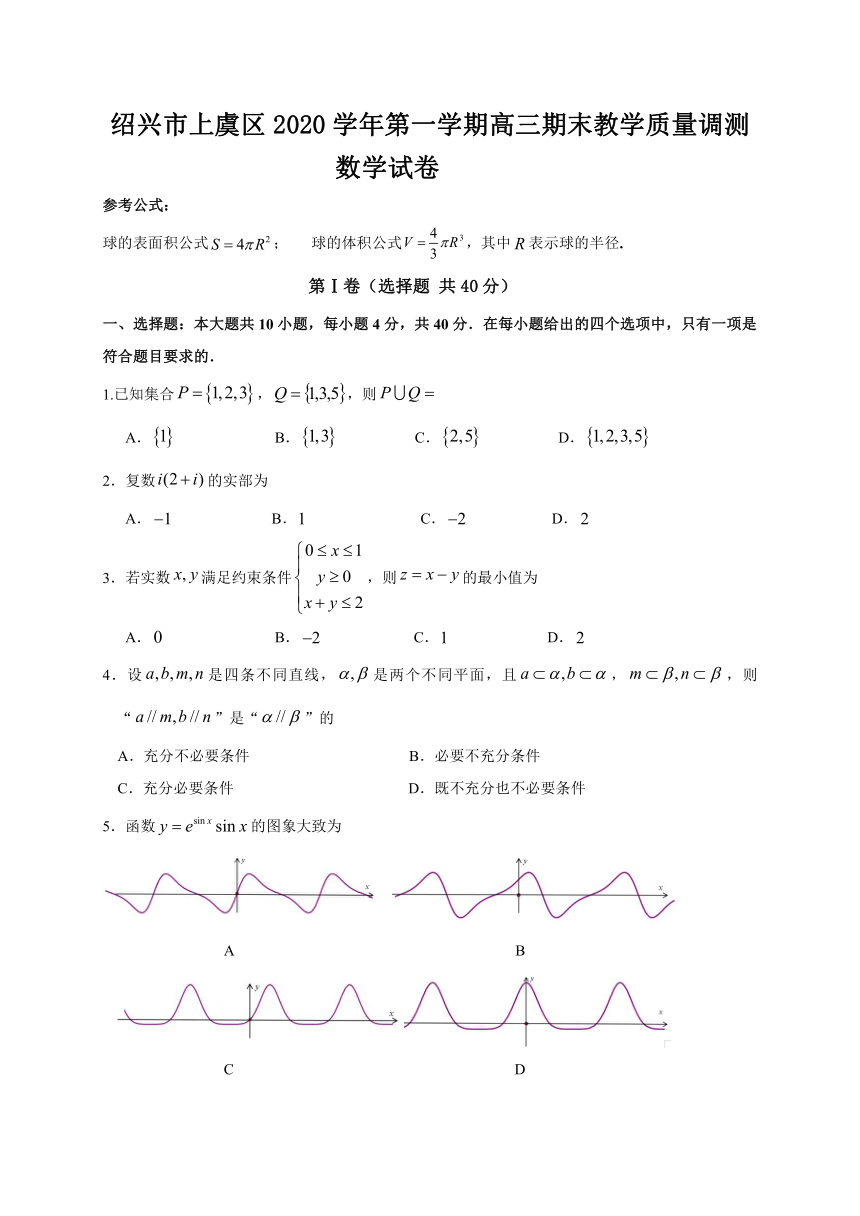 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 13:27:32 | ||
图片预览




文档简介
绍兴市上虞区2020学年第一学期高三期末教学质量调测
数学试卷
参考公式:
球的表面积公式; 球的体积公式,其中表示球的半径.
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则
A. B. C. D.
2.复数的实部为
A. B. C. D.
3.若实数满足约束条件,则的最小值为
A. B. C. D.
4.设是四条不同直线,是两个不同平面,且,,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.函数的图象大致为
A B
C D
6.函数的所有极小值点从小到大排列成数列,设是的前项和,则
A. B. C. D.
7.某几何体的三视图如图所示,且该几何体的体积为,
则正视图中的为
A. B. C. D.
8.已知圆和,动圆与圆,圆均
相切,是的内心,且,则的值为
A. B. C. D.
9.用表示非空集合中元素的个数,定义,已知集合,,且,设实数的所有可能取值构成集合,则
A. B. C. D.
10.已知函数,若对任意,存在使得
,则的最大值为
A. B. C. D.
第Ⅱ卷(非选择题共110分)
二、填空题:本大题共7小题,共36分.多空题每小题6分,单空题每小题4分.
11.双曲线的焦距等于 ▲ ;离心率是 ▲ .
12.若,则 ▲ ;_____▲ __.
13.已知角的终边与单位圆交于点且,则 ▲ ;
▲ .
14.已知函数,若,则 ▲ ;
若恒成立,则实数的取值范围是 ▲ .
15.已知且,则的最小值为 ▲ .
16.“e游小镇”某公司有A,B,C,D,E五幢独立的大楼,每两幢大楼的顶楼之间没有连接的天桥,现公司打算在这五幢楼的顶楼之间共建造3座天桥(每两幢楼的顶楼之间至多建造一座天桥),要使A楼的人员能够通过天桥走到B楼,则3座天桥的建造方法共有 ▲ 种.
17.设,,,且,是平面内两个不共线的单位向量,若向量满足,则的最大值为 ▲ .
三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)设函数.
(Ⅰ)求的最小正周期;
(Ⅱ)已知的内角,,对应的边分别为,若, 且,求的面积.
19.(本题满分15分)在四棱台中,平面,,
,,,,垂足为.
(Ⅰ)证明:平面平面;
(Ⅱ)若二面角正弦值为,求直线与平面所成角的余弦.
20.(本题满分15分)在数列,和中,为等差数列,设前项的和为,的前项和为,,,,,.
(Ⅰ)求数列的通项公式;
(Ⅱ)求证:.
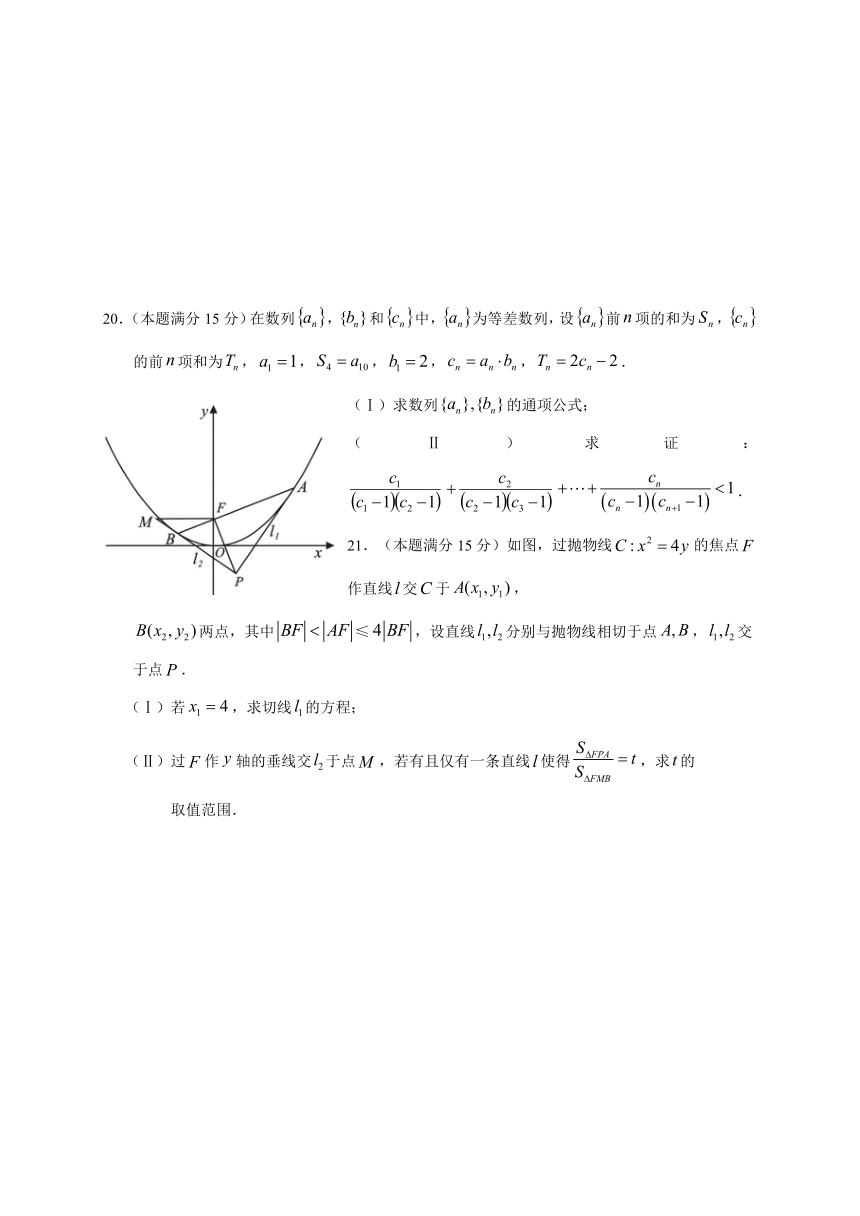
21.(本题满分15分)如图,过抛物线的焦点作直线交于,
两点,其中≤,设直线分别与抛物线相切于点,交于点.
(Ⅰ)若,求切线的方程;
(Ⅱ)过作轴的垂线交于点,若有且仅有一条直线使得,求的
取值范围.
22.(本题满分15分)已知函数有两个不同的零点().
(Ⅰ)求实数的取值范围;
(Ⅱ)记的极值点为,求证:
(i);(ii).
2020学年第一学期高三期末教学质量调测
数学参考答案(2020.2)
一、选择题:每小题4分,共40分.
1---10 DABDC BACDC
10.解析:根据题意,的值域是的值域的子集,
易知,对,只需考虑的情况,
因为,记,则
于是,从而,由得.
二、填空题:多空题每小题6分,单空题每小题4分,共36分.
11. , 12. 64,6 13., 14. 2,
15. 16.63 17.
17.解析:设,,.,则在以为直径的圆,
如图,要使得最大,四边形必须是
凸四边形,从而.
不妨固定,设,
则,,.
.
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.(14分)(Ⅰ)
-------------------4分
-------------------5分
. -------------------6分
(Ⅱ)因为,所以,则或. ----------------8分
当时,因为,
,则,
-------------------11分
当时,,
所以,则.
故的面积为或.-------------------14分
19.(15分)(Ⅰ)由,则,又平面,得,
结合,于是平面,-------------------3分
由于平面,
则①,又②,③,根据①②③,
有平面,------------6分
且平面,于是平面平面. ------------7分
(Ⅱ)法一:由(Ⅰ)知,平面,所以
直线与平面所成角为,------------9分
同时我们还得到且,因为,所以.
故直线所成的角或其补角等于二面角的大小,
易知所成的角为,于是. ------------ 12分
由(Ⅰ)知,平面,所以,故是直角梯形,
,又,,所以,
直线与平面所成角的余弦为.------------15分
法二:因为平面,,
以为原点,为轴建立
空间直角坐标系,
由(Ⅰ)知,平面,所以
直线与平面所成角为,
设.如图2,易知,,
,------------9分
设平面的法向量为,
则 ,
取,------------11分
设平面的法向量为,
则,
取, ------------13分
由题意,,
解得. ------------15分
20.(15分)(Ⅰ),
------------3分
,,
时,
,是公比为2的等比数列------------7分. ------------8分
(Ⅱ)因为
------------11分
.
------------15分
21.(Ⅰ)因为,则点,由,则,------------2分
所以的斜率等于,从而的方程是.
------------5分
(Ⅱ)设,代入抛物线,
则,从而.------------7分
设直线交于点,设,,
,则,,
而,所以.------------9分
需要来求的坐标,
由,得,于是,
即,同理得,联立两切线方程,得
,所以.
同时在中令,得,,代入的表达式,
得到, ---------12分
因为,则,结合 得,
从而,令,则且,记,
要使得有且仅有一条直线使得,则,或
所以的范围是或. ------------15分
22.(Ⅰ)由得 ------------2分
函数有两个不同的零点
在上不单调,, ------------4分
令得,故在上单调递增,
令得,故在上单调递减,
则的极大值为,.
时,时,的取值范围是. -----6分
(Ⅱ)(i)是函数的零点,
即①,要证,
只要证,即只要证,
由①,只要证,整理后即,--------8分
令 ,即证,
因为,
因为,则,故在上递增,
易知,则,所以成立. ------------10分
(ii)要证,只需证
令,则,且
下面先证明,------------12分
这只要证明,设,所以只要证明
,设,
则,所以递增,
则成立.于是得到,
因此只要证明 ,构造函数,
则,故在上递减,
在上递增,则,即成立.------------15分
数学试卷
参考公式:
球的表面积公式; 球的体积公式,其中表示球的半径.
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则
A. B. C. D.
2.复数的实部为
A. B. C. D.
3.若实数满足约束条件,则的最小值为
A. B. C. D.
4.设是四条不同直线,是两个不同平面,且,,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.函数的图象大致为
A B
C D
6.函数的所有极小值点从小到大排列成数列,设是的前项和,则
A. B. C. D.
7.某几何体的三视图如图所示,且该几何体的体积为,
则正视图中的为
A. B. C. D.
8.已知圆和,动圆与圆,圆均
相切,是的内心,且,则的值为
A. B. C. D.
9.用表示非空集合中元素的个数,定义,已知集合,,且,设实数的所有可能取值构成集合,则
A. B. C. D.
10.已知函数,若对任意,存在使得
,则的最大值为
A. B. C. D.
第Ⅱ卷(非选择题共110分)
二、填空题:本大题共7小题,共36分.多空题每小题6分,单空题每小题4分.
11.双曲线的焦距等于 ▲ ;离心率是 ▲ .
12.若,则 ▲ ;_____▲ __.
13.已知角的终边与单位圆交于点且,则 ▲ ;
▲ .
14.已知函数,若,则 ▲ ;
若恒成立,则实数的取值范围是 ▲ .
15.已知且,则的最小值为 ▲ .
16.“e游小镇”某公司有A,B,C,D,E五幢独立的大楼,每两幢大楼的顶楼之间没有连接的天桥,现公司打算在这五幢楼的顶楼之间共建造3座天桥(每两幢楼的顶楼之间至多建造一座天桥),要使A楼的人员能够通过天桥走到B楼,则3座天桥的建造方法共有 ▲ 种.
17.设,,,且,是平面内两个不共线的单位向量,若向量满足,则的最大值为 ▲ .
三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)设函数.
(Ⅰ)求的最小正周期;
(Ⅱ)已知的内角,,对应的边分别为,若, 且,求的面积.
19.(本题满分15分)在四棱台中,平面,,
,,,,垂足为.
(Ⅰ)证明:平面平面;
(Ⅱ)若二面角正弦值为,求直线与平面所成角的余弦.
20.(本题满分15分)在数列,和中,为等差数列,设前项的和为,的前项和为,,,,,.
(Ⅰ)求数列的通项公式;
(Ⅱ)求证:.
21.(本题满分15分)如图,过抛物线的焦点作直线交于,
两点,其中≤,设直线分别与抛物线相切于点,交于点.
(Ⅰ)若,求切线的方程;
(Ⅱ)过作轴的垂线交于点,若有且仅有一条直线使得,求的
取值范围.
22.(本题满分15分)已知函数有两个不同的零点().
(Ⅰ)求实数的取值范围;
(Ⅱ)记的极值点为,求证:
(i);(ii).
2020学年第一学期高三期末教学质量调测
数学参考答案(2020.2)
一、选择题:每小题4分,共40分.
1---10 DABDC BACDC
10.解析:根据题意,的值域是的值域的子集,
易知,对,只需考虑的情况,
因为,记,则
于是,从而,由得.
二、填空题:多空题每小题6分,单空题每小题4分,共36分.
11. , 12. 64,6 13., 14. 2,
15. 16.63 17.
17.解析:设,,.,则在以为直径的圆,
如图,要使得最大,四边形必须是
凸四边形,从而.
不妨固定,设,
则,,.
.
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.(14分)(Ⅰ)
-------------------4分
-------------------5分
. -------------------6分
(Ⅱ)因为,所以,则或. ----------------8分
当时,因为,
,则,
-------------------11分
当时,,
所以,则.
故的面积为或.-------------------14分
19.(15分)(Ⅰ)由,则,又平面,得,
结合,于是平面,-------------------3分
由于平面,
则①,又②,③,根据①②③,
有平面,------------6分
且平面,于是平面平面. ------------7分
(Ⅱ)法一:由(Ⅰ)知,平面,所以
直线与平面所成角为,------------9分
同时我们还得到且,因为,所以.
故直线所成的角或其补角等于二面角的大小,
易知所成的角为,于是. ------------ 12分
由(Ⅰ)知,平面,所以,故是直角梯形,
,又,,所以,
直线与平面所成角的余弦为.------------15分
法二:因为平面,,
以为原点,为轴建立
空间直角坐标系,
由(Ⅰ)知,平面,所以
直线与平面所成角为,
设.如图2,易知,,
,------------9分
设平面的法向量为,
则 ,
取,------------11分
设平面的法向量为,
则,
取, ------------13分
由题意,,
解得. ------------15分
20.(15分)(Ⅰ),
------------3分
,,
时,
,是公比为2的等比数列------------7分. ------------8分
(Ⅱ)因为
------------11分
.
------------15分
21.(Ⅰ)因为,则点,由,则,------------2分
所以的斜率等于,从而的方程是.
------------5分
(Ⅱ)设,代入抛物线,
则,从而.------------7分
设直线交于点,设,,
,则,,
而,所以.------------9分
需要来求的坐标,
由,得,于是,
即,同理得,联立两切线方程,得
,所以.
同时在中令,得,,代入的表达式,
得到, ---------12分
因为,则,结合 得,
从而,令,则且,记,
要使得有且仅有一条直线使得,则,或
所以的范围是或. ------------15分
22.(Ⅰ)由得 ------------2分
函数有两个不同的零点
在上不单调,, ------------4分
令得,故在上单调递增,
令得,故在上单调递减,
则的极大值为,.
时,时,的取值范围是. -----6分
(Ⅱ)(i)是函数的零点,
即①,要证,
只要证,即只要证,
由①,只要证,整理后即,--------8分
令 ,即证,
因为,
因为,则,故在上递增,
易知,则,所以成立. ------------10分
(ii)要证,只需证
令,则,且
下面先证明,------------12分
这只要证明,设,所以只要证明
,设,
则,所以递增,
则成立.于是得到,
因此只要证明 ,构造函数,
则,故在上递减,
在上递增,则,即成立.------------15分
同课章节目录
