2020-2021学年七年级数学苏科版下册第7章《平面图形的认识(二)》培优提升训练(一)(Word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册第7章《平面图形的认识(二)》培优提升训练(一)(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 266.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:57:50 | ||
图片预览



文档简介
苏科版七年级数学下册第7章《平面图形的认识(二)》
培优提升训练(一)
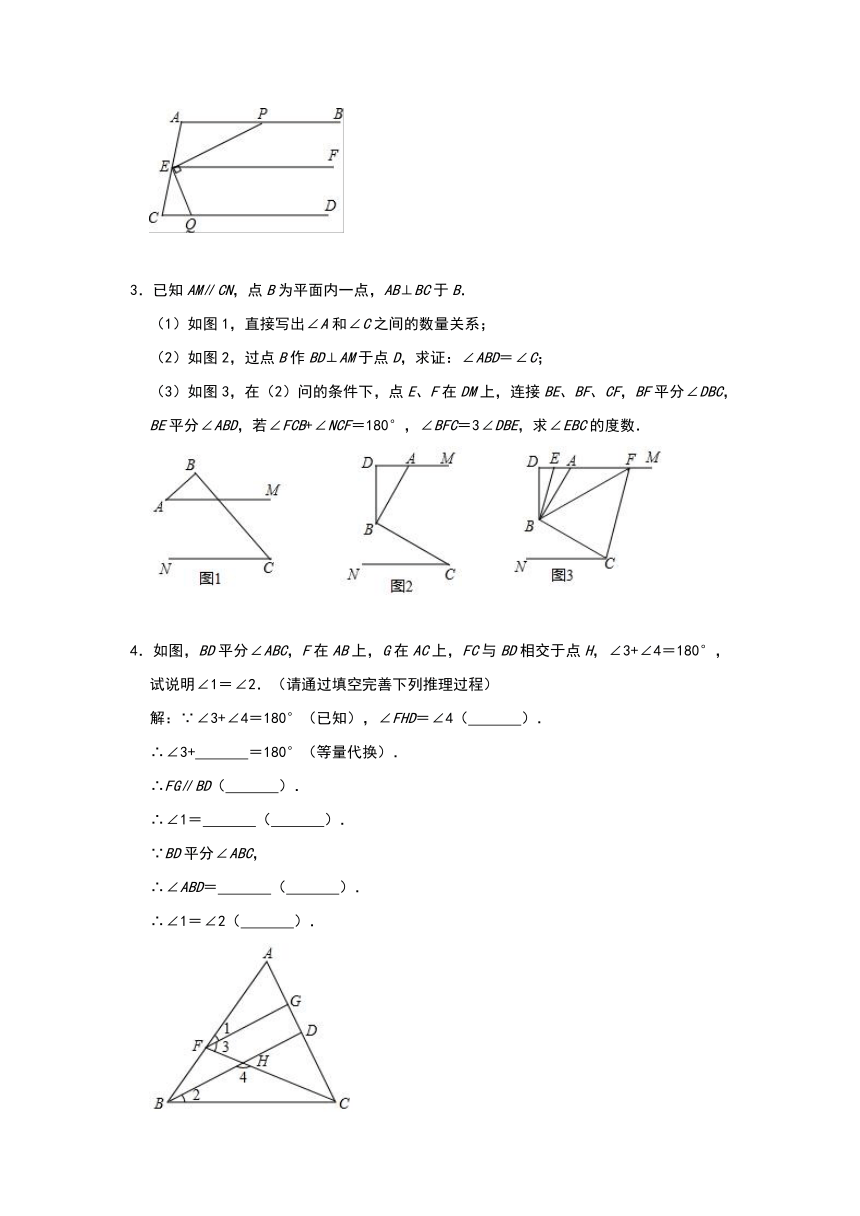
1.如图,线段AB∥CD,点P沿射线AC运动(不与A、C两点重合),连接PB、PC,作PF平分∠BPD,作PE∥AB,设∠ABP=α,∠PDC=β.
(1)如图1,当α<β,探究∠EPF与α、β的数量关系;
(2)当点P位置发生变化时,请你利用提供的图2、3、4继续操作,探究(1)中的问题.
2.完成下面推理过程.在括号内的横线上填空或填上推理依据.
如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD
证明:∵AB∥EF
∴∠APE=
(
)
∵EP⊥EQ
∴∠PEQ=
(
)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥
(
)
∴AB∥CD(
)
3.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
4.如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2.(请通过填空完善下列推理过程)
解:∵∠3+∠4=180°(已知),∠FHD=∠4(
).
∴∠3+
=180°(等量代换).
∴FG∥BD(
).
∴∠1=
(
).
∵BD平分∠ABC,
∴∠ABD=
(
).
∴∠1=∠2(
).
5.如图,在△ABC中,∠A=30°,∠ACB=80°,△ABC的外角∠CBD的平分线BE交AC的延长线于点
E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
6.如图,在△ABC中,∠B=31°,∠C=55°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE于F,求∠ADF的度数.
7.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为120°,40°,20°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=35°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=60°,求△ABC中最小内角的度数.
8.如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E;
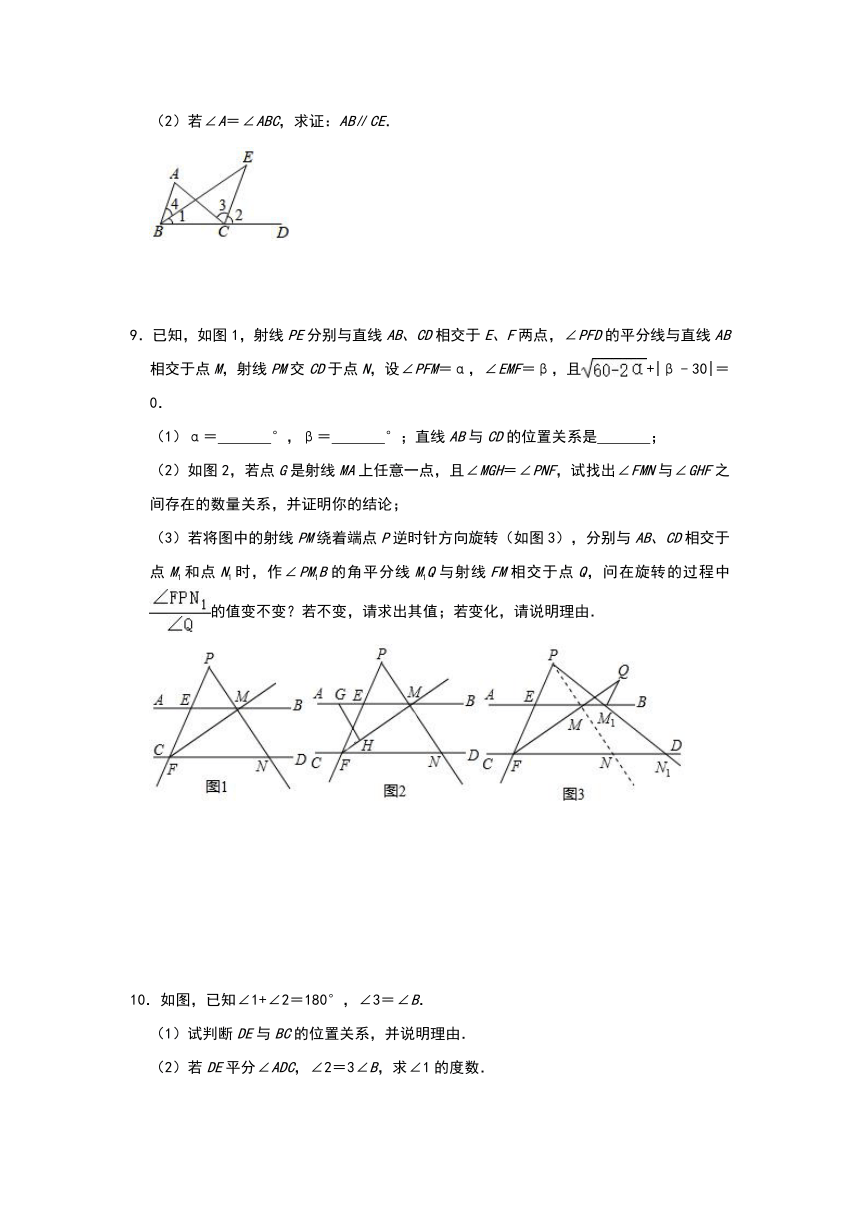
(2)若∠A=∠ABC,求证:AB∥CE.
9.已知,如图1,射线PE分别与直线AB、CD相交于E、F两点,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,设∠PFM=α,∠EMF=β,且+|β﹣30|=0.
(1)α=
°,β=
°;直线AB与CD的位置关系是
;
(2)如图2,若点G是射线MA上任意一点,且∠MGH=∠PNF,试找出∠FMN与∠GHF之间存在的数量关系,并证明你的结论;
(3)若将图中的射线PM绕着端点P逆时针方向旋转(如图3),分别与AB、CD相交于点M1和点N1时,作∠PM1B的角平分线M1Q与射线FM相交于点Q,问在旋转的过程中的值变不变?若不变,请求出其值;若变化,请说明理由.
10.如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
11.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,则有MD∥GF.下面是小颖同学的思考过程,请你在括号内填上依据.
思考过程:
因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°
(
)
所以∠BDC=∠EFC(等量代换).
所以
(同位角相等,两直线平行).
所以∠2=∠CBD
(
)
因为∠1=∠2(已知),
所以∠1=∠CBD
(
).
所以
(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°
(
),
所以MD∥BC
(
)
所以MD∥GF
(
)
12.如图,∠A+∠ABC=180°,BD⊥CD于点D,EF⊥CD于点F.
(1)请说明AD∥BC的理由;
(2)若∠ADB=45°,求∠FEC的度数.
13.如图,已知两条射线BP∥CQ,动线段AD的两个端点A、D分别在射线BP、CQ上,且∠B=∠ADC=110°,F在线段AB上,AC平分∠DCF,CE平分∠BCF.
(1)请判断AD与BC的位置关系,并说明理由;
(2)求∠ACE的度数;
(3)若平行移动AD,使∠BEC=∠CAD,求∠CAD的度数.
14.小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.
(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由.
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=50°,∠ABC=40°,求∠BED的度数.
(3)将图2中的线段BC沿DC所在的直线平移,使得点B在点A的右侧,若∠FAD=m°,∠ABC=n°,其他条件不变,得到图3,请你求出∠BED的度数(用含m,n的式子表示).
15.如图,直线MN∥GH,直线l1分别交直线MN、GH于A、B两点,直线l2分别交直线MN、GH于C、D两点,且直线l1、l2交于点E,点P是直线l2上不同于C、D、E点的动点.
(1)如图①,当点P在线段CE上时,请直写出∠NAP、∠HBP、∠APB之间的数量关系:
;
(2)如图②,当点P在线段DE上时,(1)中的∠NAP、∠HBP、∠APB之间的数量关系还成立吗?如果成立,请说明成立的理由;如果不成立,请写出这三个角之间的数量关系,并说明理由.
(3)如果点P在直线l2上且在C、D两点外侧运动时,其他条件不变,请直接写出∠NAP、∠HBP、∠APB之间的数量关系
.
参考答案
1.解:(1)如图1,∵AB∥CD,PE∥AB,∴AB∥CD∥PE,
∴∠BPE=∠ABP=α,
∠DPE=∠PDC=β,
∵PF平分∠BPD,
∴∠BPF=∠DPF,
∵∠BPF=∠BPE+∠EPF=α+∠EPF,
∠DPF=∠DPE﹣∠EPF=β﹣∠EPF,
∴α+∠EPF=β﹣∠EPF,
∴.
(2)①当α=β时,如图2,
此时∠EPF=0°.
②当点P在线段AC上,且α>β时,如图3,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
∴∠BPE=∠ABP=α,
∠DPE=∠PDC=β,
∵PF平分∠BPD,
∴∠BPF=∠DPF,
∵∠BPF=∠BPE﹣∠EPF=α﹣∠EPF,
∠DPF=∠DPE+∠EPF=β+∠EPF,
∴α﹣∠EPF=β+∠EPF,
∴.
③当点P在点C的下方时,如图4,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
∴∠BPE=∠ABP=α,
∠DPE=∠PDC=β,
∵PF平分∠BPD,
∴∠BPF=∠DPF,
∵∠BPF=∠BPE﹣∠EPF=α﹣∠EPF,
∠DPF=∠EPF﹣∠DPE=∠EPF﹣β,
∴α﹣∠EPF=∠EPF﹣β,
∴.
综上,当点P位置发生变化时,∠EPF与α、β的数量关系或.
2.证明:∵AB∥EF
∴∠APE=∠PEF(两直线平行,内错角相等)
∵EP⊥EQ
∴∠PEQ=90°(垂直的定义)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=∠QEF
∴EF∥CD(内错角相等,两直线平行)
∴AB∥CD(平行于同一直线的两直线互相平行),
故答案为:∠PEF,两直线平行,内错角相等,90°,∠QEF,内错角相等,两直线平行,CD,平行于同一直线的两直线互相平行.
3.解:
(1)如图1,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠A+∠AOB=90°,
∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,
∴∠DBG=90°,
∴∠ABD+∠ABG=90°,
∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)知∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,
则∠ABE=α,∠ABD=2α=∠CBG,
∠GBF=∠AFB=β,
∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°得:
2α+β+3α+3α+β=180°,
∵AB⊥BC,
∴β+β+2α=90°,
∴α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
4.解:∵∠3+∠4=180°(已知),∠FHD=∠4(对顶角相等),
∴∠3+∠FHD=180°(等量代换),
∴FG∥BD(同旁内角互补,两直线平行),
∴∠1=∠ABD(两直线平行,同位角相等),
∵BD平分∠ABC,
∴∠ABD=∠2(角平分线的定义),
∴∠1=∠2(等量代换),
故答案为:对顶角相等,∠FHD,同旁内角互补,两直线平行,∠ABD,两直线平行,同位角相等,∠2,角平分线的定义,等量代换.
5.解:(1)∵在△ABC中,∠A=30°,∠ACB=80°,
∴∠CBD=∠A+∠ACB=110°,
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=55°;
(2)∵∠ACB=80°,∠CBE=55°,
∴∠CEB=∠ACB﹣∠CBE=80°﹣55°=25°,
∵DF∥BE,
∴∠F=∠CEB=25°.
6.解:∵∠B=31°,∠C=55°,
∴∠BAC=94°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=47°,
∴∠AED=∠B+∠BAE=31°+47°=78°,
∵AD⊥BC,DF⊥AE,
∴∠EFD=∠ADE=90°,
∴∠AED+∠EDF=∠EDF+∠ADF,
∴∠ADF=∠AED=78°.
7.解:(1)△ABC是“三倍角三角形”,理由如下:
∵∠A=35°,∠B=40°,
∴∠C=180°﹣35°﹣40°=105°=35°×3,
∴△ABC是“三倍角三角形”;
(2)∵∠B=60°,
∴∠A+∠C=120°,
设最小的角为x,
①当60°=3x时,x=20°,
②当x+3x=120°时,x=30°,
答:△ABC中最小内角为20°或30°.
8.证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知),
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(三角形外角的性质),
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质),
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知),
∴∠ACD=2∠2,∠ABC=2∠1(角平分线的性质
),
∴∠A=2∠2﹣2∠1(
等量代换),
=2(∠2﹣∠1)(提取公因数),
=2∠E(等量代换);
(2)由(1)可知:∠A=2∠E
∵∠A=∠ABC,∠ABC=2∠ABE,
∴2∠E=2∠ABE,
即∠E=∠ABE,
∴AB∥CE.
9.(1)证明:∵+|β﹣30|=0,
∴α=β=30,
∴∠PFM=∠MFN=30°,∠EMF=30°,
∴∠EMF=∠MFN,
∴AB∥CD;
故答案为:30;30;AB∥CD;
(2)解:∠FMN+∠GHF=180°.
理由:∵AB∥CD,
∴∠MNF=∠PME,
∵∠MGH=∠MNF,
∴∠PME=∠MGH,
∴GH∥PN,
∴∠GHM=∠FMN,
∵∠GHF+∠GHM=180°,
∴∠FMN+∠GHF=180°.
(3)解:的值不变,=2.
理由:如图3中,作∠PEM1的平分线交M1Q的延长线于R.
∵AB∥CD,
∴∠PEM1=∠PFN,
∵∠PER=∠PEM1,∠PFQ=∠PFN,
∴∠PER=∠PFQ,
∴ER∥FQ,
∴∠FQM1=∠R,
设∠PER=∠REB=x,∠PM1R=∠RM1B=y,
则有:,可得∠EPM1=2∠R,
∴∠EPM1=2∠FQM1
∴=2.
10.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
11.解:因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°(垂直的定义),
所以∠BDC=∠EFC(等量代换),
所以BD∥EF(同位角相等,两直线平行),
所以∠2=∠CBD(两直线平行,同位角相等),
因为∠1=∠2(已知),
所以∠1=∠CBD(等量代换),
所以BC∥GF(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°(已知),
所以MD∥GF(同旁内角互补,两直线平行),
所以DM∥BC(平行于同一条直线的两条直线平行);
故答案为:垂直的定义;BD∥EF;两直线平行,同位角相等;等量代换;BC∥GF;已知;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
12.解:如图所示:
(1)AD∥BC的理由如下:
∵∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行);
(2)∵BD⊥CD,
∴∠BDC=90°,
∵AD∥BC,
∴∠ADB=∠DBC,
又∵∠ADB=45°,
∴∠DBC=45°,
又∵BD⊥CD.EF⊥CD,
∴BD∥EF,
∴∠DBC=∠FEC,
∴∠FEC=45°.
13.解:(1)结论:AD∥BC.
理由:∵BP∥CQ,
∴∠DCB=180°﹣∠B=180°﹣110°=70°,
∵∠ADC+∠DCB=110°+70°=180°,
∴AD∥BC.
(2)∵AC平分∠DCF,CE平分∠BCF,
∴∠ACF=∠DCF,∠FCE=∠FCB,
∴∠ACE=∠ACF+∠FCE=∠DCF+∠FCB=∠DCB=×70°=35°.
(3)设∠ACD=x,
∵AB∥CD,
∴∠BEC=∠DCE=35°+x,
∵AD∥BC,
∴∠DAC=∠ACB=70°﹣x,
则有35°+x=(70°﹣x),
解得x=28°,
∴∠CAD=70°﹣28°=42°.
14.解:(1)如图1中,作EF∥AB,则有EF∥CD,
∴∠1=∠BAE,∠2=∠DCE,
∴∠AEC=∠1+∠2=∠BAE+∠DCE.
(2)如图2,过点E作EH∥AB,
∵AB∥CD,∠FAD=50°,
∴∠FAD=∠ADC=50°,
∵DE平分∠ADC,∠ADC=50°,
∴∠EDC=∠ADC=25°,
∵BE平分∠ABC,∠ABC=40°,
∴∠ABE=∠ABC=20°,
∵AB∥CD,
∴AB∥CD∥EH,
∴∠ABE=∠BEH=20°,∠CDE=∠DEH=25°,
∴∠BED=∠BEH+∠DEH=45°.
(3)∠BED的度数改变.
过点E作EG∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=∠FAD=m°
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=m°
∵AB∥CD,
∴AB∥CD∥EG,
∴∠BEG=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEG=m°,
∴∠BED=∠BEG+∠DEG=180°﹣n°+m°.
15.解:(1)如图①,过P点作PQ∥GH,
∵MN∥GH,
∴MN∥PQ∥GH,
∴∠APQ=∠NAP,
∠BPQ=∠HBP,
∵∠APB=∠APQ+∠BPQ,
∴∠APB=∠NAP+∠HBP;
(2)如图②,过P点作PQ∥GH,
∵MN∥GH,
∴MN∥PQ∥GH,
∴∠APQ+∠NAP=180°,
∠BPQ+∠HBP=180°,
∵∠APB=∠APQ+∠BPQ,
∴∠APB=(180°﹣∠NAP)+(180°﹣∠HBP)=360°﹣(∠NAP+∠HBP);
(3)如备用图,
∵MN∥GH,
∴∠PFN=∠HBP,
∵∠PFN=∠NAP+∠APB,
∴∠HBP=∠NAP+∠APB.
如备用图,
∵MN∥GH,
∴∠PFB=∠NAP,
∵∠HBP=∠PFB+∠APB,
∴∠HBP=∠NAP+∠APB.
故答案为:∠APB=∠NAP+∠HBP;∠HBP=∠NAP+∠APB.
培优提升训练(一)
1.如图,线段AB∥CD,点P沿射线AC运动(不与A、C两点重合),连接PB、PC,作PF平分∠BPD,作PE∥AB,设∠ABP=α,∠PDC=β.
(1)如图1,当α<β,探究∠EPF与α、β的数量关系;
(2)当点P位置发生变化时,请你利用提供的图2、3、4继续操作,探究(1)中的问题.
2.完成下面推理过程.在括号内的横线上填空或填上推理依据.
如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD
证明:∵AB∥EF
∴∠APE=
(
)
∵EP⊥EQ
∴∠PEQ=
(
)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥
(
)
∴AB∥CD(
)
3.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
4.如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2.(请通过填空完善下列推理过程)
解:∵∠3+∠4=180°(已知),∠FHD=∠4(
).
∴∠3+
=180°(等量代换).
∴FG∥BD(
).
∴∠1=
(
).
∵BD平分∠ABC,
∴∠ABD=
(
).
∴∠1=∠2(
).
5.如图,在△ABC中,∠A=30°,∠ACB=80°,△ABC的外角∠CBD的平分线BE交AC的延长线于点
E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
6.如图,在△ABC中,∠B=31°,∠C=55°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE于F,求∠ADF的度数.
7.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为120°,40°,20°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=35°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=60°,求△ABC中最小内角的度数.
8.如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E;
(2)若∠A=∠ABC,求证:AB∥CE.
9.已知,如图1,射线PE分别与直线AB、CD相交于E、F两点,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,设∠PFM=α,∠EMF=β,且+|β﹣30|=0.
(1)α=
°,β=
°;直线AB与CD的位置关系是
;
(2)如图2,若点G是射线MA上任意一点,且∠MGH=∠PNF,试找出∠FMN与∠GHF之间存在的数量关系,并证明你的结论;
(3)若将图中的射线PM绕着端点P逆时针方向旋转(如图3),分别与AB、CD相交于点M1和点N1时,作∠PM1B的角平分线M1Q与射线FM相交于点Q,问在旋转的过程中的值变不变?若不变,请求出其值;若变化,请说明理由.
10.如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
11.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,则有MD∥GF.下面是小颖同学的思考过程,请你在括号内填上依据.
思考过程:
因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°
(
)
所以∠BDC=∠EFC(等量代换).
所以
(同位角相等,两直线平行).
所以∠2=∠CBD
(
)
因为∠1=∠2(已知),
所以∠1=∠CBD
(
).
所以
(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°
(
),
所以MD∥BC
(
)
所以MD∥GF
(
)
12.如图,∠A+∠ABC=180°,BD⊥CD于点D,EF⊥CD于点F.
(1)请说明AD∥BC的理由;
(2)若∠ADB=45°,求∠FEC的度数.
13.如图,已知两条射线BP∥CQ,动线段AD的两个端点A、D分别在射线BP、CQ上,且∠B=∠ADC=110°,F在线段AB上,AC平分∠DCF,CE平分∠BCF.
(1)请判断AD与BC的位置关系,并说明理由;
(2)求∠ACE的度数;
(3)若平行移动AD,使∠BEC=∠CAD,求∠CAD的度数.
14.小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.
(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由.
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=50°,∠ABC=40°,求∠BED的度数.
(3)将图2中的线段BC沿DC所在的直线平移,使得点B在点A的右侧,若∠FAD=m°,∠ABC=n°,其他条件不变,得到图3,请你求出∠BED的度数(用含m,n的式子表示).
15.如图,直线MN∥GH,直线l1分别交直线MN、GH于A、B两点,直线l2分别交直线MN、GH于C、D两点,且直线l1、l2交于点E,点P是直线l2上不同于C、D、E点的动点.
(1)如图①,当点P在线段CE上时,请直写出∠NAP、∠HBP、∠APB之间的数量关系:
;
(2)如图②,当点P在线段DE上时,(1)中的∠NAP、∠HBP、∠APB之间的数量关系还成立吗?如果成立,请说明成立的理由;如果不成立,请写出这三个角之间的数量关系,并说明理由.
(3)如果点P在直线l2上且在C、D两点外侧运动时,其他条件不变,请直接写出∠NAP、∠HBP、∠APB之间的数量关系
.
参考答案
1.解:(1)如图1,∵AB∥CD,PE∥AB,∴AB∥CD∥PE,
∴∠BPE=∠ABP=α,
∠DPE=∠PDC=β,
∵PF平分∠BPD,
∴∠BPF=∠DPF,
∵∠BPF=∠BPE+∠EPF=α+∠EPF,
∠DPF=∠DPE﹣∠EPF=β﹣∠EPF,
∴α+∠EPF=β﹣∠EPF,
∴.
(2)①当α=β时,如图2,
此时∠EPF=0°.
②当点P在线段AC上,且α>β时,如图3,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
∴∠BPE=∠ABP=α,
∠DPE=∠PDC=β,
∵PF平分∠BPD,
∴∠BPF=∠DPF,
∵∠BPF=∠BPE﹣∠EPF=α﹣∠EPF,
∠DPF=∠DPE+∠EPF=β+∠EPF,
∴α﹣∠EPF=β+∠EPF,
∴.
③当点P在点C的下方时,如图4,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
∴∠BPE=∠ABP=α,
∠DPE=∠PDC=β,
∵PF平分∠BPD,
∴∠BPF=∠DPF,
∵∠BPF=∠BPE﹣∠EPF=α﹣∠EPF,
∠DPF=∠EPF﹣∠DPE=∠EPF﹣β,
∴α﹣∠EPF=∠EPF﹣β,
∴.
综上,当点P位置发生变化时,∠EPF与α、β的数量关系或.
2.证明:∵AB∥EF
∴∠APE=∠PEF(两直线平行,内错角相等)
∵EP⊥EQ
∴∠PEQ=90°(垂直的定义)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=∠QEF
∴EF∥CD(内错角相等,两直线平行)
∴AB∥CD(平行于同一直线的两直线互相平行),
故答案为:∠PEF,两直线平行,内错角相等,90°,∠QEF,内错角相等,两直线平行,CD,平行于同一直线的两直线互相平行.
3.解:
(1)如图1,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠A+∠AOB=90°,
∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,
∴∠DBG=90°,
∴∠ABD+∠ABG=90°,
∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)知∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,
则∠ABE=α,∠ABD=2α=∠CBG,
∠GBF=∠AFB=β,
∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°得:
2α+β+3α+3α+β=180°,
∵AB⊥BC,
∴β+β+2α=90°,
∴α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
4.解:∵∠3+∠4=180°(已知),∠FHD=∠4(对顶角相等),
∴∠3+∠FHD=180°(等量代换),
∴FG∥BD(同旁内角互补,两直线平行),
∴∠1=∠ABD(两直线平行,同位角相等),
∵BD平分∠ABC,
∴∠ABD=∠2(角平分线的定义),
∴∠1=∠2(等量代换),
故答案为:对顶角相等,∠FHD,同旁内角互补,两直线平行,∠ABD,两直线平行,同位角相等,∠2,角平分线的定义,等量代换.
5.解:(1)∵在△ABC中,∠A=30°,∠ACB=80°,
∴∠CBD=∠A+∠ACB=110°,
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=55°;
(2)∵∠ACB=80°,∠CBE=55°,
∴∠CEB=∠ACB﹣∠CBE=80°﹣55°=25°,
∵DF∥BE,
∴∠F=∠CEB=25°.
6.解:∵∠B=31°,∠C=55°,
∴∠BAC=94°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=47°,
∴∠AED=∠B+∠BAE=31°+47°=78°,
∵AD⊥BC,DF⊥AE,
∴∠EFD=∠ADE=90°,
∴∠AED+∠EDF=∠EDF+∠ADF,
∴∠ADF=∠AED=78°.
7.解:(1)△ABC是“三倍角三角形”,理由如下:
∵∠A=35°,∠B=40°,
∴∠C=180°﹣35°﹣40°=105°=35°×3,
∴△ABC是“三倍角三角形”;
(2)∵∠B=60°,
∴∠A+∠C=120°,
设最小的角为x,
①当60°=3x时,x=20°,
②当x+3x=120°时,x=30°,
答:△ABC中最小内角为20°或30°.
8.证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知),
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(三角形外角的性质),
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质),
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知),
∴∠ACD=2∠2,∠ABC=2∠1(角平分线的性质
),
∴∠A=2∠2﹣2∠1(
等量代换),
=2(∠2﹣∠1)(提取公因数),
=2∠E(等量代换);
(2)由(1)可知:∠A=2∠E
∵∠A=∠ABC,∠ABC=2∠ABE,
∴2∠E=2∠ABE,
即∠E=∠ABE,
∴AB∥CE.
9.(1)证明:∵+|β﹣30|=0,
∴α=β=30,
∴∠PFM=∠MFN=30°,∠EMF=30°,
∴∠EMF=∠MFN,
∴AB∥CD;
故答案为:30;30;AB∥CD;
(2)解:∠FMN+∠GHF=180°.
理由:∵AB∥CD,
∴∠MNF=∠PME,
∵∠MGH=∠MNF,
∴∠PME=∠MGH,
∴GH∥PN,
∴∠GHM=∠FMN,
∵∠GHF+∠GHM=180°,
∴∠FMN+∠GHF=180°.
(3)解:的值不变,=2.
理由:如图3中,作∠PEM1的平分线交M1Q的延长线于R.
∵AB∥CD,
∴∠PEM1=∠PFN,
∵∠PER=∠PEM1,∠PFQ=∠PFN,
∴∠PER=∠PFQ,
∴ER∥FQ,
∴∠FQM1=∠R,
设∠PER=∠REB=x,∠PM1R=∠RM1B=y,
则有:,可得∠EPM1=2∠R,
∴∠EPM1=2∠FQM1
∴=2.
10.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
11.解:因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°(垂直的定义),
所以∠BDC=∠EFC(等量代换),
所以BD∥EF(同位角相等,两直线平行),
所以∠2=∠CBD(两直线平行,同位角相等),
因为∠1=∠2(已知),
所以∠1=∠CBD(等量代换),
所以BC∥GF(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°(已知),
所以MD∥GF(同旁内角互补,两直线平行),
所以DM∥BC(平行于同一条直线的两条直线平行);
故答案为:垂直的定义;BD∥EF;两直线平行,同位角相等;等量代换;BC∥GF;已知;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
12.解:如图所示:
(1)AD∥BC的理由如下:
∵∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行);
(2)∵BD⊥CD,
∴∠BDC=90°,
∵AD∥BC,
∴∠ADB=∠DBC,
又∵∠ADB=45°,
∴∠DBC=45°,
又∵BD⊥CD.EF⊥CD,
∴BD∥EF,
∴∠DBC=∠FEC,
∴∠FEC=45°.
13.解:(1)结论:AD∥BC.
理由:∵BP∥CQ,
∴∠DCB=180°﹣∠B=180°﹣110°=70°,
∵∠ADC+∠DCB=110°+70°=180°,
∴AD∥BC.
(2)∵AC平分∠DCF,CE平分∠BCF,
∴∠ACF=∠DCF,∠FCE=∠FCB,
∴∠ACE=∠ACF+∠FCE=∠DCF+∠FCB=∠DCB=×70°=35°.
(3)设∠ACD=x,
∵AB∥CD,
∴∠BEC=∠DCE=35°+x,
∵AD∥BC,
∴∠DAC=∠ACB=70°﹣x,
则有35°+x=(70°﹣x),
解得x=28°,
∴∠CAD=70°﹣28°=42°.
14.解:(1)如图1中,作EF∥AB,则有EF∥CD,
∴∠1=∠BAE,∠2=∠DCE,
∴∠AEC=∠1+∠2=∠BAE+∠DCE.
(2)如图2,过点E作EH∥AB,
∵AB∥CD,∠FAD=50°,
∴∠FAD=∠ADC=50°,
∵DE平分∠ADC,∠ADC=50°,
∴∠EDC=∠ADC=25°,
∵BE平分∠ABC,∠ABC=40°,
∴∠ABE=∠ABC=20°,
∵AB∥CD,
∴AB∥CD∥EH,
∴∠ABE=∠BEH=20°,∠CDE=∠DEH=25°,
∴∠BED=∠BEH+∠DEH=45°.
(3)∠BED的度数改变.
过点E作EG∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=∠FAD=m°
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=m°
∵AB∥CD,
∴AB∥CD∥EG,
∴∠BEG=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEG=m°,
∴∠BED=∠BEG+∠DEG=180°﹣n°+m°.
15.解:(1)如图①,过P点作PQ∥GH,
∵MN∥GH,
∴MN∥PQ∥GH,
∴∠APQ=∠NAP,
∠BPQ=∠HBP,
∵∠APB=∠APQ+∠BPQ,
∴∠APB=∠NAP+∠HBP;
(2)如图②,过P点作PQ∥GH,
∵MN∥GH,
∴MN∥PQ∥GH,
∴∠APQ+∠NAP=180°,
∠BPQ+∠HBP=180°,
∵∠APB=∠APQ+∠BPQ,
∴∠APB=(180°﹣∠NAP)+(180°﹣∠HBP)=360°﹣(∠NAP+∠HBP);
(3)如备用图,
∵MN∥GH,
∴∠PFN=∠HBP,
∵∠PFN=∠NAP+∠APB,
∴∠HBP=∠NAP+∠APB.
如备用图,
∵MN∥GH,
∴∠PFB=∠NAP,
∵∠HBP=∠PFB+∠APB,
∴∠HBP=∠NAP+∠APB.
故答案为:∠APB=∠NAP+∠HBP;∠HBP=∠NAP+∠APB.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
