高二数学立体几何试题及答案
图片预览



文档简介
【模拟试题】
一. 选择题(每小题5分,共60分)
1. 给出四个命题:
①各侧面都是正方形的棱柱一定是正棱柱;
②各对角面是全等矩形的平行六面体一定是长方体;
③有两个侧面垂直于底面的棱柱一定是直棱柱;
④长方体一定是正四棱柱。
其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
2. 下列四个命题:
①各侧面是全等的等腰三角形的四棱锥是正四棱锥;
②底面是正多边形的棱锥是正棱锥;
③棱锥的所有面可能都是直角三角形;
④四棱锥中侧面最多有四个直角三角形。
正确的命题有________个
A. 1 B. 2 C. 3 D. 4
3. 长方体的一个顶点处的三条棱长之比为1:2:3,它的表面积为88,则它的对角线长为( )
A. 12 B. 24 C. D.
4. 湖面上漂着一个球,湖结冰后将球取出,冰面上留下一个面直径为24cm,深为8cm的空穴,则该球的半径是( )
A. 8cm B. 12cm C. 13cm D.
5. 一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积为侧面积的比是( )
A. B. C. D.
6. 已知直线,有下面四个命题:
①;②;③;④。
其中正确的两个命题是( )
A. ①② B. ③④ C. ②④ D. ①③
7. 若干毫升水倒入底面半径为2cm的圆柱形器皿中,量得水面的高度为6cm,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是( )
A. B. C. D.
8. 设正方体的全面积为,一个球内切于该正方体,那么这个球的体积是( )
A. B. C. D.
9. 对于直线m、n和平面能得出的一个条件是( )
A. B.
C. D.
10. 如果直线l、m与平面满足:,那么必有( )
A. B.
C. D.
11. 已知正方体的八个顶点中,有四个点恰好为正四面体的顶点,则该正四面体的体积与正方体的体积之比为( )
A. B. C. 2:3 D. 1:3
12. 向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是( )
二. 填空题(每小题4分,共16分)
13. 正方体的全面积是,它的顶点都在球面上,这个球的表面积是__________。
14. 正四棱台的斜高与上、下底面边长之比为5:2:8,体积为,则棱台的高为____________。
15. 正三棱柱的底面边长为a,过它的一条侧棱上相距为b的两点作两个互相平行的截面,在这两个截面间的斜三棱柱的侧面积为____________。
16. 已知是两个不同的平面,m、n是平面之外的两条不同的直线,给出四个论断:
①m⊥n,②,③,④。
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______________。
三. 解答题(共74分)
17. (12分)正方体中,E、F、G分别是棱DA、DC、的中点,试找出过正方体的三个顶点且与平面EFG平行的平面,并证明之。
18. (12分)球内有相距1cm的两个平行截面,截面的面积分别是,球心不在截面之间,求球的表面积与体积。
19. (12分)一个正三棱柱的三视图如图所示,求这个正三棱锥的表面积。
20. (12分)直角梯形的一个内角为45°,下底长为上底长的,这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是(),求这个旋转体的体积。
21. (12分)有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇形ABCD,作圆台形容器的侧面,并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面)。(如图)试求
(1)AD应取多长?
(2)容器的容积。
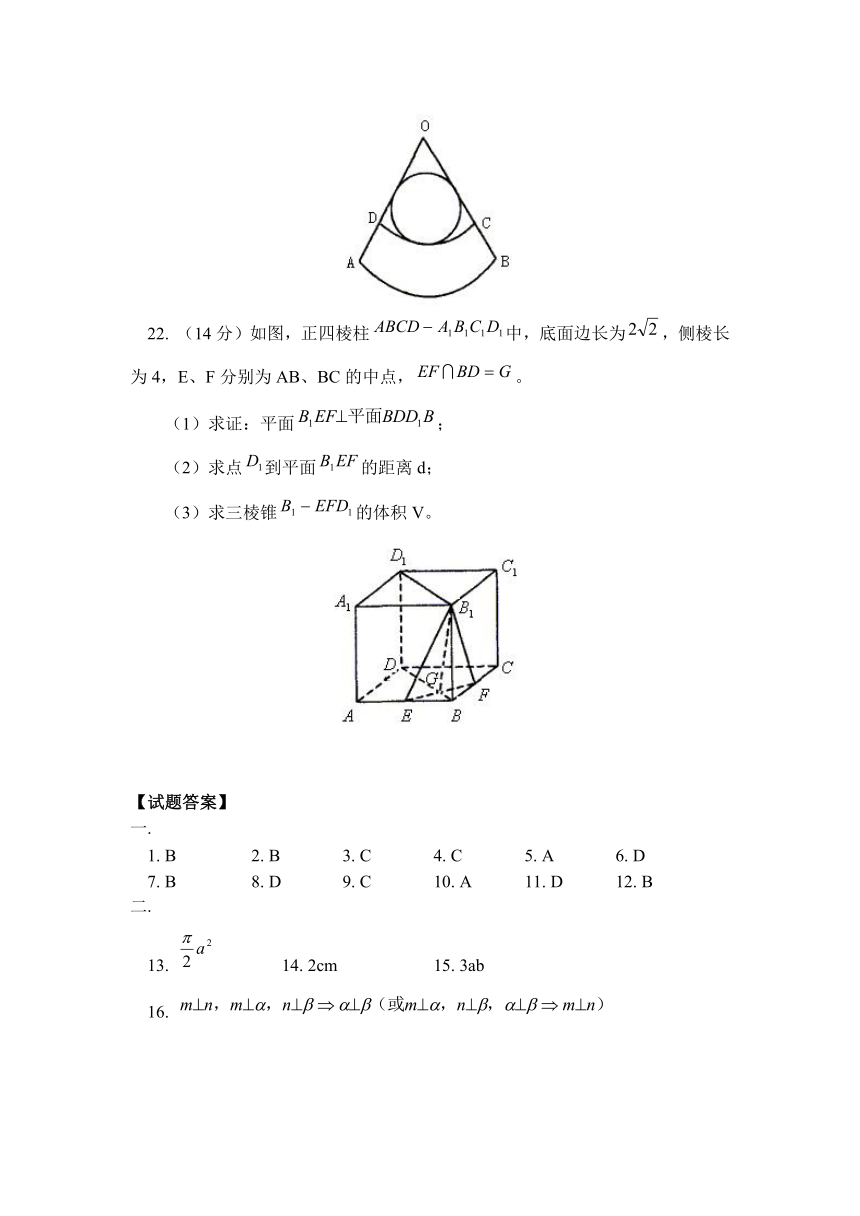
22. (14分)如图,正四棱柱中,底面边长为,侧棱长为4,E、F分别为AB、BC的中点,。
(1)求证:平面;
(2)求点到平面的距离d;
(3)求三棱锥的体积V。
【试题答案】
一.
1. B 2. B 3. C 4. C 5. A 6. D
7. B 8. D 9. C 10. A 11. D 12. B
二.
13. 14. 2cm 15. 3ab
16.
三.
17. 证明:过的平面与平面EFG平行,由E、F、G是棱DA、DC、的中点可得GE//,GF//,平面EFG,平面EFG
∴//平面AEG,//平面EFG
又
∴平面EFG//平面
18. 解:如图,设两平行截面半径分别为
依题意,
19. 解:由三视图知正三棱锥的高为2mm
由左视图知正三棱锥的底面三角形的高为
设底面边长为a,则
∴正三棱柱的表面积
20. 解:如图,梯形ABCD,AB//CD,∠A=90°,∠B=45°,绕AB边旋转一周后形成一圆柱和一圆锥的组合体。
设
根据题设
所以旋转体体积
21. 解:如图,设圆台上、下底面半径分别为r、R、AD=x,则
由题意得
(2)又圆台的高h=
22. 证明:(1)如图,连结AC
∵正四棱柱的底面呈正方形
∴AC⊥BD
又AC⊥
∴AC⊥平面
∵E、F分别为AB、BC的中点
∴EF//AC
∴EF⊥平面
∴平面
解(2)在对角面中,作,垂足为H
∵平面,且平面平面
∴
∴为点到平面的距离
在Rt△中,
(2)
一. 选择题(每小题5分,共60分)
1. 给出四个命题:
①各侧面都是正方形的棱柱一定是正棱柱;
②各对角面是全等矩形的平行六面体一定是长方体;
③有两个侧面垂直于底面的棱柱一定是直棱柱;
④长方体一定是正四棱柱。
其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
2. 下列四个命题:
①各侧面是全等的等腰三角形的四棱锥是正四棱锥;
②底面是正多边形的棱锥是正棱锥;
③棱锥的所有面可能都是直角三角形;
④四棱锥中侧面最多有四个直角三角形。
正确的命题有________个
A. 1 B. 2 C. 3 D. 4
3. 长方体的一个顶点处的三条棱长之比为1:2:3,它的表面积为88,则它的对角线长为( )
A. 12 B. 24 C. D.
4. 湖面上漂着一个球,湖结冰后将球取出,冰面上留下一个面直径为24cm,深为8cm的空穴,则该球的半径是( )
A. 8cm B. 12cm C. 13cm D.
5. 一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积为侧面积的比是( )
A. B. C. D.
6. 已知直线,有下面四个命题:
①;②;③;④。
其中正确的两个命题是( )
A. ①② B. ③④ C. ②④ D. ①③
7. 若干毫升水倒入底面半径为2cm的圆柱形器皿中,量得水面的高度为6cm,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是( )
A. B. C. D.
8. 设正方体的全面积为,一个球内切于该正方体,那么这个球的体积是( )
A. B. C. D.
9. 对于直线m、n和平面能得出的一个条件是( )
A. B.
C. D.
10. 如果直线l、m与平面满足:,那么必有( )
A. B.
C. D.
11. 已知正方体的八个顶点中,有四个点恰好为正四面体的顶点,则该正四面体的体积与正方体的体积之比为( )
A. B. C. 2:3 D. 1:3
12. 向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是( )
二. 填空题(每小题4分,共16分)
13. 正方体的全面积是,它的顶点都在球面上,这个球的表面积是__________。
14. 正四棱台的斜高与上、下底面边长之比为5:2:8,体积为,则棱台的高为____________。
15. 正三棱柱的底面边长为a,过它的一条侧棱上相距为b的两点作两个互相平行的截面,在这两个截面间的斜三棱柱的侧面积为____________。
16. 已知是两个不同的平面,m、n是平面之外的两条不同的直线,给出四个论断:
①m⊥n,②,③,④。
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______________。
三. 解答题(共74分)
17. (12分)正方体中,E、F、G分别是棱DA、DC、的中点,试找出过正方体的三个顶点且与平面EFG平行的平面,并证明之。
18. (12分)球内有相距1cm的两个平行截面,截面的面积分别是,球心不在截面之间,求球的表面积与体积。
19. (12分)一个正三棱柱的三视图如图所示,求这个正三棱锥的表面积。
20. (12分)直角梯形的一个内角为45°,下底长为上底长的,这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是(),求这个旋转体的体积。
21. (12分)有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇形ABCD,作圆台形容器的侧面,并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面)。(如图)试求
(1)AD应取多长?
(2)容器的容积。
22. (14分)如图,正四棱柱中,底面边长为,侧棱长为4,E、F分别为AB、BC的中点,。
(1)求证:平面;
(2)求点到平面的距离d;
(3)求三棱锥的体积V。
【试题答案】
一.
1. B 2. B 3. C 4. C 5. A 6. D
7. B 8. D 9. C 10. A 11. D 12. B
二.
13. 14. 2cm 15. 3ab
16.
三.
17. 证明:过的平面与平面EFG平行,由E、F、G是棱DA、DC、的中点可得GE//,GF//,平面EFG,平面EFG
∴//平面AEG,//平面EFG
又
∴平面EFG//平面
18. 解:如图,设两平行截面半径分别为
依题意,
19. 解:由三视图知正三棱锥的高为2mm
由左视图知正三棱锥的底面三角形的高为
设底面边长为a,则
∴正三棱柱的表面积
20. 解:如图,梯形ABCD,AB//CD,∠A=90°,∠B=45°,绕AB边旋转一周后形成一圆柱和一圆锥的组合体。
设
根据题设
所以旋转体体积
21. 解:如图,设圆台上、下底面半径分别为r、R、AD=x,则
由题意得
(2)又圆台的高h=
22. 证明:(1)如图,连结AC
∵正四棱柱的底面呈正方形
∴AC⊥BD
又AC⊥
∴AC⊥平面
∵E、F分别为AB、BC的中点
∴EF//AC
∴EF⊥平面
∴平面
解(2)在对角面中,作,垂足为H
∵平面,且平面平面
∴
∴为点到平面的距离
在Rt△中,
(2)
