2020—2021学年人教版数学八年级下册18.1.2平行四边形的判定课件(22张)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册18.1.2平行四边形的判定课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 578.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
第十八章
平行四边形
三角形的中位线(一)
学习目标
能够运用中位线进行有关的证明和计算。
进一步提高几何推理能力。
情境引入:
如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点间的距离?根据是什么?
前面我们研究平行四边形时,常常把
它分成几个三角形,利用三角形全等的性
质研究平行四边形的有关问题。下面我们
利用平行四边形研究三角形的有关问题。
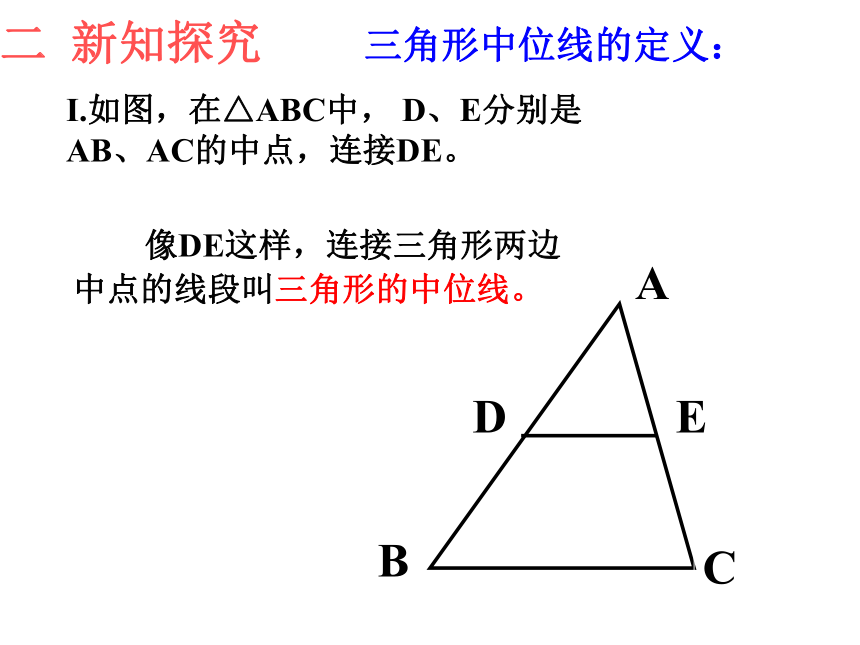
Ⅰ.如图,在△ABC中,
D、E分别是
AB、AC的中点,连接DE。
A
B
C
D
E
三角形中位线的定义:
像DE这样,连接三角形两边
中点的线段叫三角形的中位线。
二
新知探究
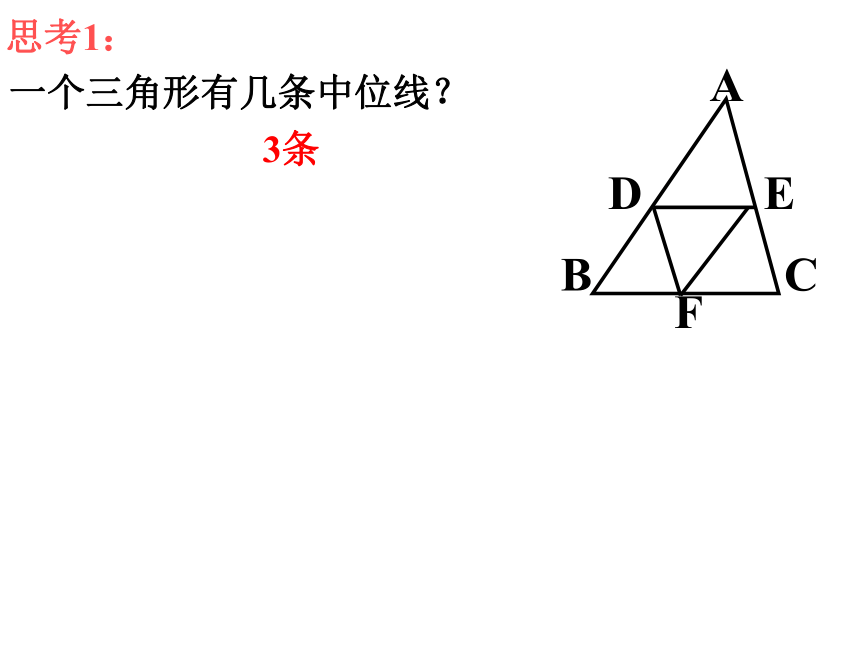
思考1:
A
B
C
D
E
∴DE
一个三角形有几条中位线?
3条
F
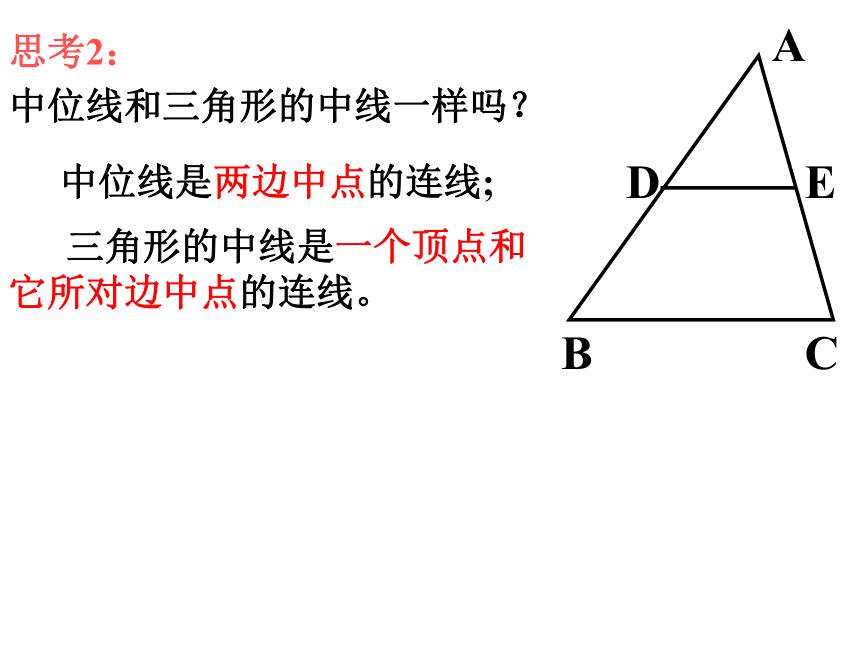
思考2:
中位线和三角形的中线一样吗?
A
B
C
D
E
∴DE
中位线是两边中点的连线;
三角形的中线是一个顶点和
它所对边中点的连线。
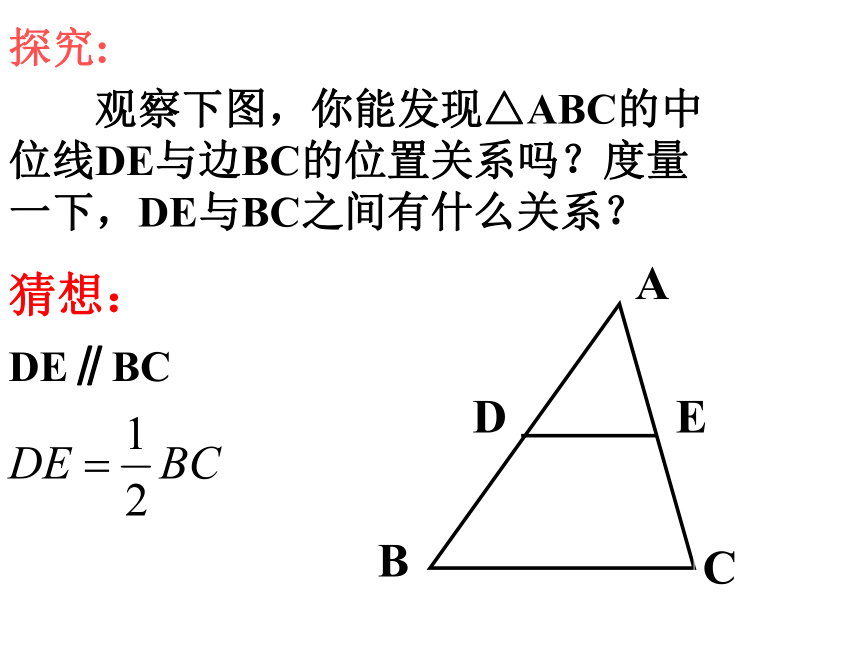
探究:
观察下图,你能发现△ABC的中
位线DE与边BC的位置关系吗?度量
一下,DE与BC之间有什么关系?
A
B
C
D
E
DE∥BC
猜想:
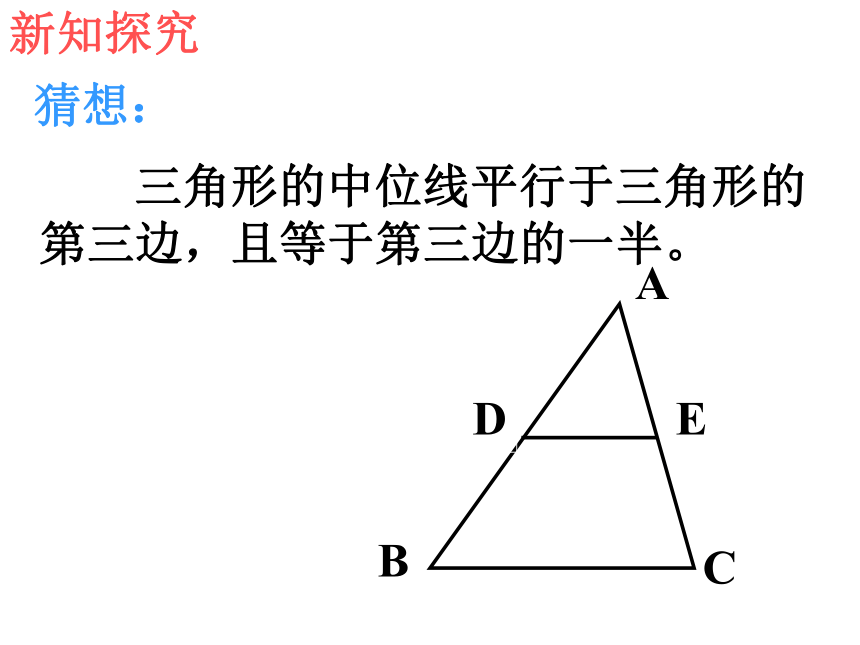
猜想:
三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
A
B
C
D
E
新知探究
证明:三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
求证:DE∥BC,DE=
BC。
A
B
C
D
E
已知:如图△ABC中,D、E是△ABC的边AB、AC的中点。
F
中线(中位线)加倍法
求证:DE∥BC,DE=
BC。
A
B
C
D
E
已知:如图△ABC中,D、E是△ABC的边AB、AC的中点。
F
证明:方法1
延长DE至F,使EF=DE,连接CF
∵D、E是分别是AB、AC的中点
∴AE=CE,AD=BD
在△AED和△CEF中
DE=EF
∴△AED≌△CEF(SAS)
AE=CE
∠AED=∠CEF
BD∥CF
∴四边形DBCF是平
行四边形
DF∥BC
求证:DE∥BC,DE=
BC。
A
B
C
D
E
已知:如图△ABC中,D、E是△ABC
的边AB、AC的中点。
F
证明:方法2
延长DE至F,使EF=DE,连接CF,AF,CD.
∵D、E是分别是AB、AC的中点
∴AE=CE,AD=BD
AD∥CF
∴四边形ADCF是平行四边形
BD∥CF
∴四边形DBCF是平行四边形
DF∥BC
∴DE∥BC
归纳
三角形中位线定理:
三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
A
B
C
D
E
几何语言:
∵DE是⊿ABC的中位线
∴DE
∴DE∥BC,
典型例题
例1、如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点间的距离?根据是什么?
则AB=2a.
解:
取AC的中点E,BC的中点F,
连接EF,
量得EF的长,
则A、B两点间的距离可求出
理由如下:
∵E,F分别是AC,BC的中点
∴EF是△ABC的中位线
∴EF=1/2AB
设EF=a,
测量不能直接到达两点间距离的方法
例2.如图,任意四边形ABCD各边的中点
E、F、G、H,若对角线AC+BD=40,则四
边形EFGH的周长是________.
B
40
D
A
C
E
F
G
H
∴GH、HE、EF、GF分别是⊿ADC
、⊿ADB、⊿ABC、⊿CBD的中位线。
四
活学活用
A
B
C
D
E
1、在△ABC中,D、E分别是AB、AC的中点。
(1)若DE=2,则BC=_______
(2)若BC=10,则DE=__________
4
5
2.如图,□ABCD中,点E是
边CD的中点,若OE=5cm,则
AD之长为_______cm.
D
A
B
C
E
O
10
A
B
C
D
E
3、在△ABC中,D、E分别是AB、
AC的中点。若∠ADE=60°,
∠A=50°
则∠C=_______.
70°
4.如图,在⊿ABC中,点D、E、F
分别是AB、BC、CA的中点,且⊿ABC
的周长为30cm,则⊿DEF的周长是___cm.
D
A
B
C
E
F
15
(1)DE=2cm,DF=3cm,EF=4cm,求⊿ABC的周长
变式:
(2)AC=6,BC=8,AB=10,求⊿DEF的面积。
18
6
五
拓展延伸:1.如图,在⊿ABC中,中线BD、CE交于点O,F、G分别是OB、OC的中点。
求证:四边形DEFG为平行四边形。
A
B
C
E
D
G
F
O
证明:
∵BD、CE是中线,F、G分别是OB、OC的中点
∴DE、FG分别是⊿ABC
和⊿OBC的中位线。
∴DE∥BC,
FG∥BC,
∴DE∥FG,
∴四边形DEFG为平行四边形
2.如图,□ABCD的对角线AC、BD相交于点O,
E、F、G、H分别是OA、OB、OC、OD的中点。求证:四边形EFGH是平行四边形。
D
A
B
C
E
F
G
H
o
证明:
∵E、F、G、H分别是OA、OB、OC、OD的中点
∴EH、FG分别是⊿OAD
和⊿OBC的中位线。
∴EH∥AD,
FG∥BC,
∴EH∥FG,
∴四边形EFGH为平行四边形
小结:
1.三角形中位线的定义:
连接三角形两边中点的线段叫三
角形的中位线。
2.三角形中位线定理:
三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
第十八章
平行四边形
三角形的中位线(一)
学习目标
能够运用中位线进行有关的证明和计算。
进一步提高几何推理能力。
情境引入:
如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点间的距离?根据是什么?
前面我们研究平行四边形时,常常把
它分成几个三角形,利用三角形全等的性
质研究平行四边形的有关问题。下面我们
利用平行四边形研究三角形的有关问题。
Ⅰ.如图,在△ABC中,
D、E分别是
AB、AC的中点,连接DE。
A
B
C
D
E
三角形中位线的定义:
像DE这样,连接三角形两边
中点的线段叫三角形的中位线。
二
新知探究
思考1:
A
B
C
D
E
∴DE
一个三角形有几条中位线?
3条
F
思考2:
中位线和三角形的中线一样吗?
A
B
C
D
E
∴DE
中位线是两边中点的连线;
三角形的中线是一个顶点和
它所对边中点的连线。
探究:
观察下图,你能发现△ABC的中
位线DE与边BC的位置关系吗?度量
一下,DE与BC之间有什么关系?
A
B
C
D
E
DE∥BC
猜想:
猜想:
三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
A
B
C
D
E
新知探究
证明:三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
求证:DE∥BC,DE=
BC。
A
B
C
D
E
已知:如图△ABC中,D、E是△ABC的边AB、AC的中点。
F
中线(中位线)加倍法
求证:DE∥BC,DE=
BC。
A
B
C
D
E
已知:如图△ABC中,D、E是△ABC的边AB、AC的中点。
F
证明:方法1
延长DE至F,使EF=DE,连接CF
∵D、E是分别是AB、AC的中点
∴AE=CE,AD=BD
在△AED和△CEF中
DE=EF
∴△AED≌△CEF(SAS)
AE=CE
∠AED=∠CEF
BD∥CF
∴四边形DBCF是平
行四边形
DF∥BC
求证:DE∥BC,DE=
BC。
A
B
C
D
E
已知:如图△ABC中,D、E是△ABC
的边AB、AC的中点。
F
证明:方法2
延长DE至F,使EF=DE,连接CF,AF,CD.
∵D、E是分别是AB、AC的中点
∴AE=CE,AD=BD
AD∥CF
∴四边形ADCF是平行四边形
BD∥CF
∴四边形DBCF是平行四边形
DF∥BC
∴DE∥BC
归纳
三角形中位线定理:
三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
A
B
C
D
E
几何语言:
∵DE是⊿ABC的中位线
∴DE
∴DE∥BC,
典型例题
例1、如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点间的距离?根据是什么?
则AB=2a.
解:
取AC的中点E,BC的中点F,
连接EF,
量得EF的长,
则A、B两点间的距离可求出
理由如下:
∵E,F分别是AC,BC的中点
∴EF是△ABC的中位线
∴EF=1/2AB
设EF=a,
测量不能直接到达两点间距离的方法
例2.如图,任意四边形ABCD各边的中点
E、F、G、H,若对角线AC+BD=40,则四
边形EFGH的周长是________.
B
40
D
A
C
E
F
G
H
∴GH、HE、EF、GF分别是⊿ADC
、⊿ADB、⊿ABC、⊿CBD的中位线。
四
活学活用
A
B
C
D
E
1、在△ABC中,D、E分别是AB、AC的中点。
(1)若DE=2,则BC=_______
(2)若BC=10,则DE=__________
4
5
2.如图,□ABCD中,点E是
边CD的中点,若OE=5cm,则
AD之长为_______cm.
D
A
B
C
E
O
10
A
B
C
D
E
3、在△ABC中,D、E分别是AB、
AC的中点。若∠ADE=60°,
∠A=50°
则∠C=_______.
70°
4.如图,在⊿ABC中,点D、E、F
分别是AB、BC、CA的中点,且⊿ABC
的周长为30cm,则⊿DEF的周长是___cm.
D
A
B
C
E
F
15
(1)DE=2cm,DF=3cm,EF=4cm,求⊿ABC的周长
变式:
(2)AC=6,BC=8,AB=10,求⊿DEF的面积。
18
6
五
拓展延伸:1.如图,在⊿ABC中,中线BD、CE交于点O,F、G分别是OB、OC的中点。
求证:四边形DEFG为平行四边形。
A
B
C
E
D
G
F
O
证明:
∵BD、CE是中线,F、G分别是OB、OC的中点
∴DE、FG分别是⊿ABC
和⊿OBC的中位线。
∴DE∥BC,
FG∥BC,
∴DE∥FG,
∴四边形DEFG为平行四边形
2.如图,□ABCD的对角线AC、BD相交于点O,
E、F、G、H分别是OA、OB、OC、OD的中点。求证:四边形EFGH是平行四边形。
D
A
B
C
E
F
G
H
o
证明:
∵E、F、G、H分别是OA、OB、OC、OD的中点
∴EH、FG分别是⊿OAD
和⊿OBC的中位线。
∴EH∥AD,
FG∥BC,
∴EH∥FG,
∴四边形EFGH为平行四边形
小结:
1.三角形中位线的定义:
连接三角形两边中点的线段叫三
角形的中位线。
2.三角形中位线定理:
三角形的中位线平行于三角形的
第三边,且等于第三边的一半。
