2020—2021学年人教版数学八年级下册第十八章:平行四边形复习课课件(21张)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册第十八章:平行四边形复习课课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览

文档简介
(共21张PPT)
第十八章
平行四边形
第十八章:平行四边形
复习课
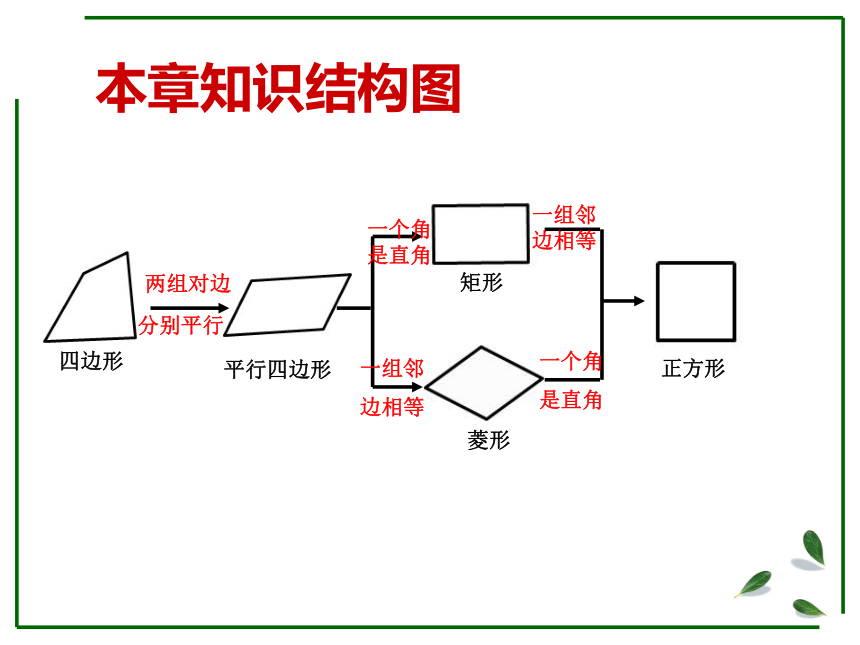
四边形
两组对边
分别平行
平行四边形
矩形
菱形
正方形
一个角是直角
一组邻
边相等
一组邻边相等
一个角
是直角
本章知识结构图
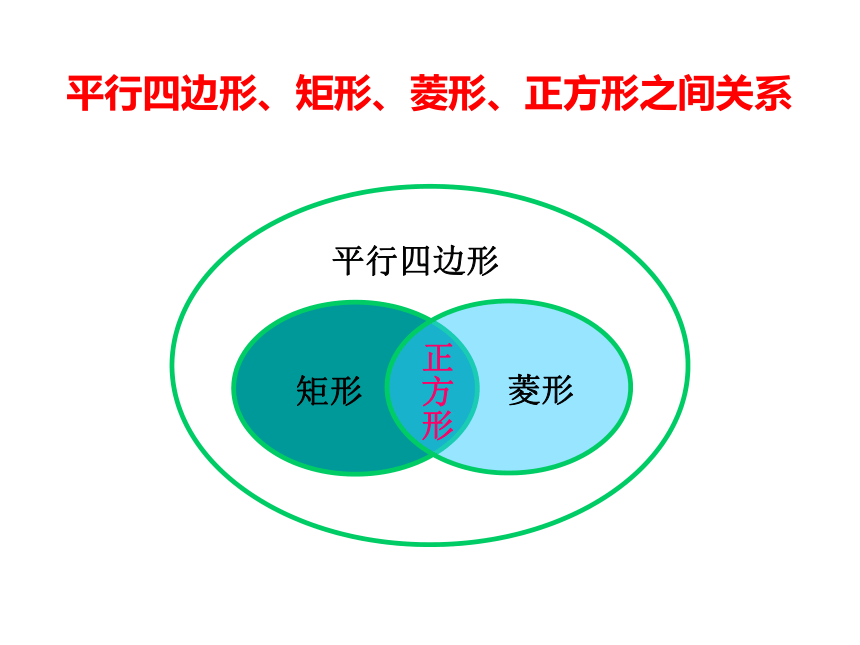
平行四边形
矩形
菱形
正方形
平行四边形、矩形、菱形、正方形之间关系
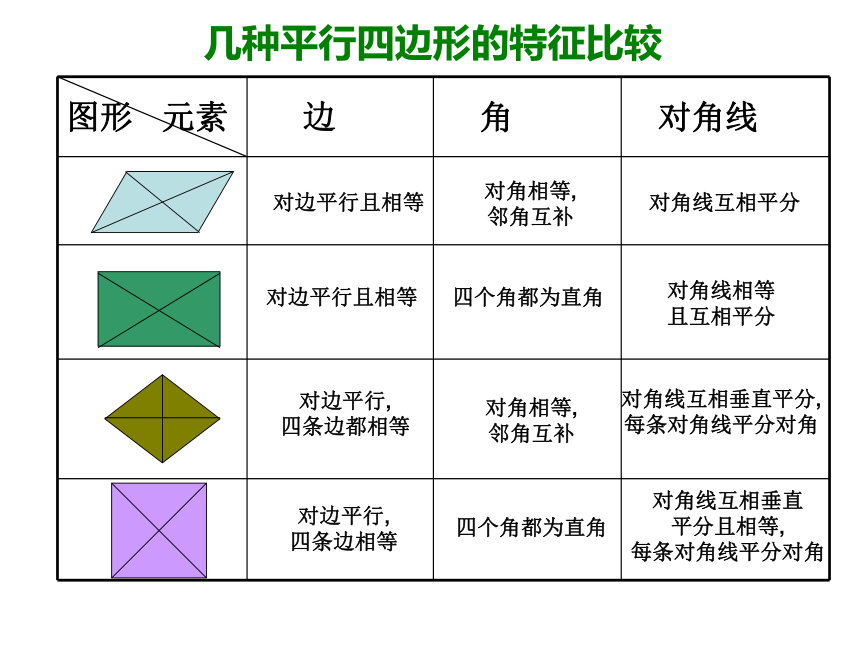
几种平行四边形的特征比较
图形
元素
边
角
对角线
对边平行且相等
对边平行且相等
对边平行,
四条边都相等
对边平行,
四条边相等
对角相等,
邻角互补
四个角都为直角
对角相等,
邻角互补
四个角都为直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,
每条对角线平分对角
对角线互相垂直
平分且相等,
每条对角线平分对角
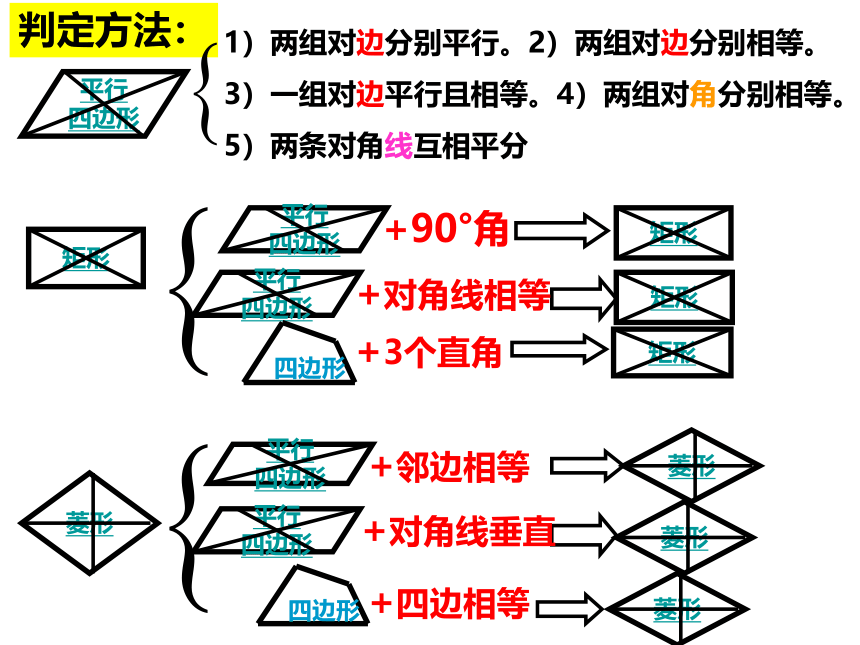
1)两组对边分别平行。2)两组对边分别相等。
3)一组对边平行且相等。4)两组对角分别相等。
5)两条对角线互相平分
矩形
菱形
平行
四边形
平行
四边形
+90°角
矩形
+对角线相等
平行
四边形
矩形
四边形
+3个直角
矩形
平行
四边形
+邻边相等
菱形
+对角线垂直
平行
四边形
菱形
四边形
+四边相等
菱形
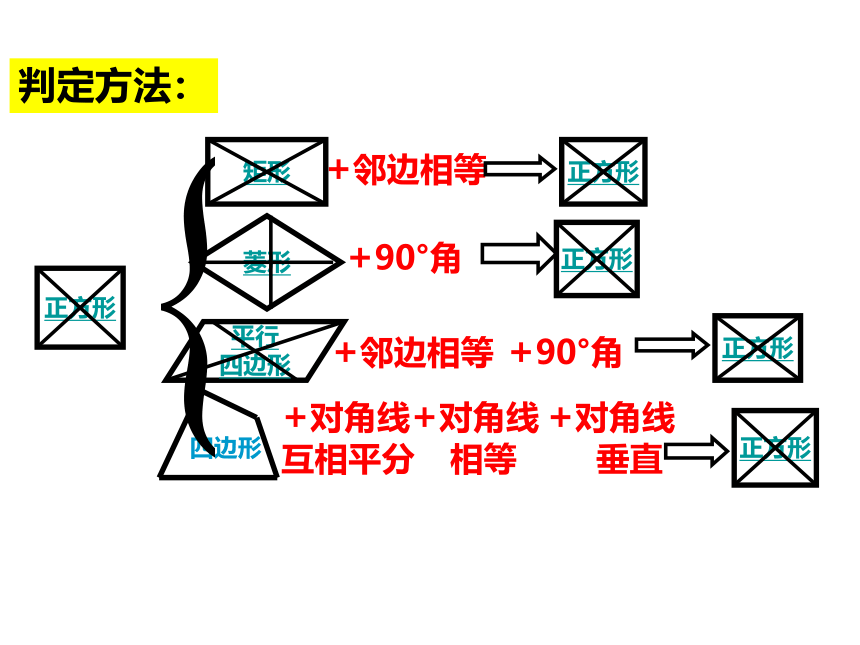
判定方法:
+邻边相等
+90°角
+对角线
互相平分
正方形
矩形
菱形
正方形
平行
四边形
正方形
四边形
正方形
+邻边相等
+90°角
+对角线
相等
+对角线
垂直
判定方法:
正方形
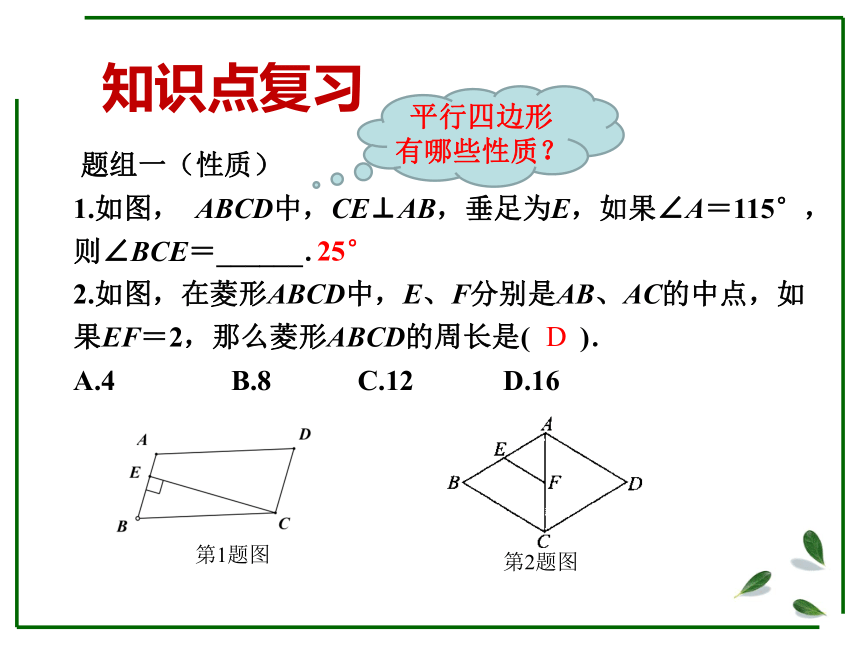
知识点复习
第1题图
第2题图
25°
D
题组一(性质)
1.如图,
ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=______.
2.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是(
).
A.4
B.8
C.12
D.16
平行四边形有哪些性质?
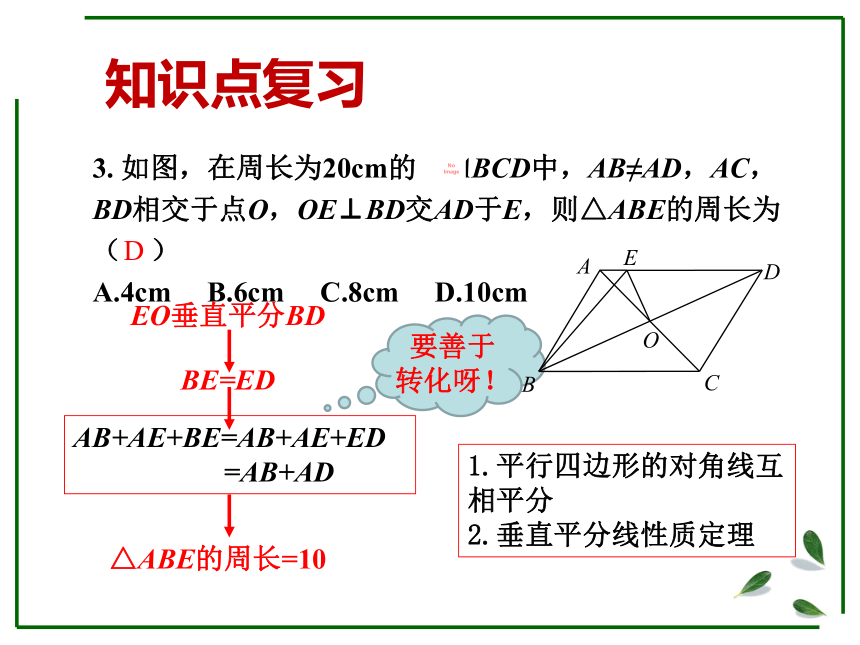
知识点复习
3.
如图,在周长为20cm的
ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为(
)
A.4cm
B.6cm
C.8cm
D.10cm
EO垂直平分BD
BE=ED
AB+AE+BE=AB+AE+ED
=AB+AD
△ABE的周长=10
要善于转化呀!
1.平行四边形的对角线互相平分
2.垂直平分线性质定理
A
B
C
D
O
E
D
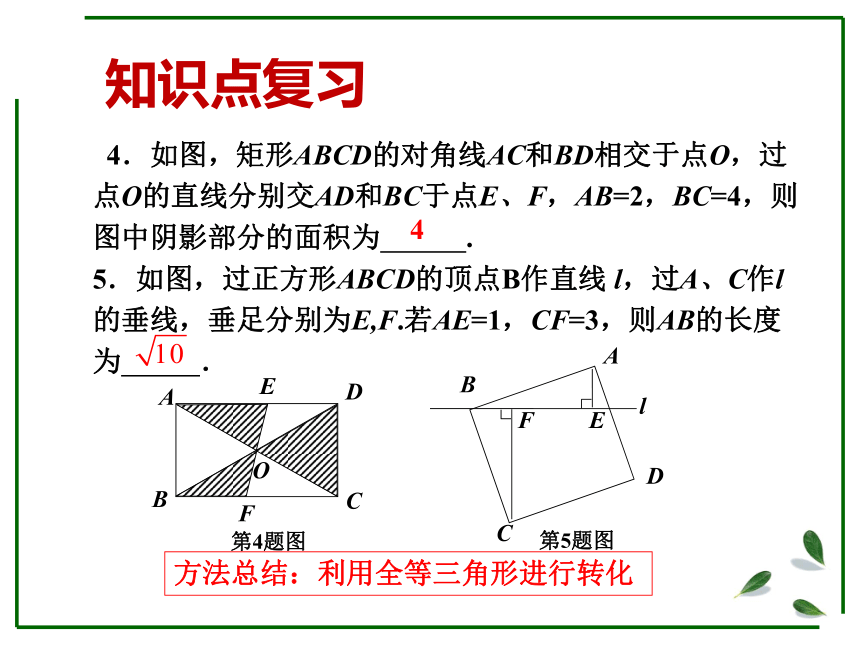
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为
.
5.如图,过正方形ABCD的顶点B作直线
l,过A、C作l
的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为
.
知识点复习
A
B
C
D
E
F
l
第4题图
第5题图
A
O
D
C
B
F
E
4
方法总结:利用全等三角形进行转化
6.如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2.求(1)∠ABC的度数;(2)对角线AC、BD的长;(3)菱形ABCD的面积.
知识点复习
解:(1)
∠ABC=
120°
(2)BD=2,AC=
(3)菱形ABCD面积=
菱形面积=底×高=对角线乘积的一半
所有对角线垂直的四边形都可以用此方法求面积
7、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为________
8、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于(
)
A.15°B.30°C.45°
D.60°
9、把一张长方形的纸条按图那样折叠,若得到
∠AME=70o
,则∠EMN=(
)
A、45o
B、50o
C、55o
D、60o
知识点复习
题组二(判定应用)
已知:如图,E、F为
ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法)
?
?
?
?
?
?
?
知识点复习
解题思路
方法一:
通过证明△ABE≌△CDF
,
得到BE=DF.
题组二(判定应用)
例1
已知:如图,E、F为
ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法)
?
?
?
?
?
?
?
知识点复习
方法二:
通过证明四边形BFDE是平行四边形,
得到BE=DF.
证明线段相等的方法有哪些?
例2
如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF,请你猜想:
BE与DF有怎样的关系?
并对你的猜想加以证明
A
B
C
D
E
F
知识点复习
猜想:BE∥DF,BE=DF
A
B
C
D
E
F
o
D
A
B
C
E
F
1
2
3
4
题组三(综合应用)
四边形ABCD和四边形CEFH都是正方形,连接AF,M是AF中点,连接DM和EM.探究线段DM与EM的位置关系,并求
的值.小聪同学的思路是:延长DM交EF于点N,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)如图,当点B、C、H在一条直线上时,线段DM与EM的位置关系是
,
=
;z````x``xk
?
?
?
?
?
?
?
知识点复习
解题思路:延长DM与EF交与N
证明△ADM≌△FNM
DM=MN,
AD=NF
EM⊥DN
又
∵∠DEN=90°
DM=NM
∴
∴
思路:中点构造八字全等
题组三(综合应用)
四边形ABCD和四边形CEFH都是正方形,连接AF,M是AF中点,连接DM和EM.探究线段DM与EM的位置关系,并求
的值.小聪同学的思路是:延长DM交EF于点N,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(2)如图,当点B、C、F在一条直线上时,
(1)中的结论还成立吗?如果成立,
请证明;如果不成立,说明理由.
?
?
?
?
?
?
知识点复习
知识点复习
△AMD≌△FMN
AD=FN=DC,DM=NM.
∠2=∠EFC=
45°
EC=EF
△EDC≌△ENF
ED=EN
DM⊥EM
∠3=∠4
∠DEN=90°
解题思路
课堂练习
1.
如图,四边形ABCD是正方形,AE⊥BE于点E,且AE=3,BE=4,则阴影部分的面积是_________________.
?
2.
如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF.
第1题图
第2题图
课堂练习
3.
如图,矩形ABCD
的对角线AC、BD
相交于点O,CE⊥BO
于E,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
4.如图,在菱形
ABCD和菱形BEFG
中,点A、B、E
在同一条直线上,
P是线段DF的中点,连结PG、PC
,若∠ABC=∠BEF=
60°,求证:
.
:
第3题图
第4题图
1.本节课复习了哪些数学知识?
总结反思
2.在解决问题的过程中突出的数学思想方法是什么?
平行四边形的问题往往转化为三角形来解决,同时平行四边形又为三角形全等提供边等和角等.
3.畅所欲言:本节课中你有什么收获?还有什么疑惑呢?
第十八章
平行四边形
第十八章:平行四边形
复习课
四边形
两组对边
分别平行
平行四边形
矩形
菱形
正方形
一个角是直角
一组邻
边相等
一组邻边相等
一个角
是直角
本章知识结构图
平行四边形
矩形
菱形
正方形
平行四边形、矩形、菱形、正方形之间关系
几种平行四边形的特征比较
图形
元素
边
角
对角线
对边平行且相等
对边平行且相等
对边平行,
四条边都相等
对边平行,
四条边相等
对角相等,
邻角互补
四个角都为直角
对角相等,
邻角互补
四个角都为直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,
每条对角线平分对角
对角线互相垂直
平分且相等,
每条对角线平分对角
1)两组对边分别平行。2)两组对边分别相等。
3)一组对边平行且相等。4)两组对角分别相等。
5)两条对角线互相平分
矩形
菱形
平行
四边形
平行
四边形
+90°角
矩形
+对角线相等
平行
四边形
矩形
四边形
+3个直角
矩形
平行
四边形
+邻边相等
菱形
+对角线垂直
平行
四边形
菱形
四边形
+四边相等
菱形
判定方法:
+邻边相等
+90°角
+对角线
互相平分
正方形
矩形
菱形
正方形
平行
四边形
正方形
四边形
正方形
+邻边相等
+90°角
+对角线
相等
+对角线
垂直
判定方法:
正方形
知识点复习
第1题图
第2题图
25°
D
题组一(性质)
1.如图,
ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=______.
2.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是(
).
A.4
B.8
C.12
D.16
平行四边形有哪些性质?
知识点复习
3.
如图,在周长为20cm的
ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为(
)
A.4cm
B.6cm
C.8cm
D.10cm
EO垂直平分BD
BE=ED
AB+AE+BE=AB+AE+ED
=AB+AD
△ABE的周长=10
要善于转化呀!
1.平行四边形的对角线互相平分
2.垂直平分线性质定理
A
B
C
D
O
E
D
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为
.
5.如图,过正方形ABCD的顶点B作直线
l,过A、C作l
的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为
.
知识点复习
A
B
C
D
E
F
l
第4题图
第5题图
A
O
D
C
B
F
E
4
方法总结:利用全等三角形进行转化
6.如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2.求(1)∠ABC的度数;(2)对角线AC、BD的长;(3)菱形ABCD的面积.
知识点复习
解:(1)
∠ABC=
120°
(2)BD=2,AC=
(3)菱形ABCD面积=
菱形面积=底×高=对角线乘积的一半
所有对角线垂直的四边形都可以用此方法求面积
7、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为________
8、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于(
)
A.15°B.30°C.45°
D.60°
9、把一张长方形的纸条按图那样折叠,若得到
∠AME=70o
,则∠EMN=(
)
A、45o
B、50o
C、55o
D、60o
知识点复习
题组二(判定应用)
已知:如图,E、F为
ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法)
?
?
?
?
?
?
?
知识点复习
解题思路
方法一:
通过证明△ABE≌△CDF
,
得到BE=DF.
题组二(判定应用)
例1
已知:如图,E、F为
ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法)
?
?
?
?
?
?
?
知识点复习
方法二:
通过证明四边形BFDE是平行四边形,
得到BE=DF.
证明线段相等的方法有哪些?
例2
如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF,请你猜想:
BE与DF有怎样的关系?
并对你的猜想加以证明
A
B
C
D
E
F
知识点复习
猜想:BE∥DF,BE=DF
A
B
C
D
E
F
o
D
A
B
C
E
F
1
2
3
4
题组三(综合应用)
四边形ABCD和四边形CEFH都是正方形,连接AF,M是AF中点,连接DM和EM.探究线段DM与EM的位置关系,并求
的值.小聪同学的思路是:延长DM交EF于点N,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)如图,当点B、C、H在一条直线上时,线段DM与EM的位置关系是
,
=
;z````x``xk
?
?
?
?
?
?
?
知识点复习
解题思路:延长DM与EF交与N
证明△ADM≌△FNM
DM=MN,
AD=NF
EM⊥DN
又
∵∠DEN=90°
DM=NM
∴
∴
思路:中点构造八字全等
题组三(综合应用)
四边形ABCD和四边形CEFH都是正方形,连接AF,M是AF中点,连接DM和EM.探究线段DM与EM的位置关系,并求
的值.小聪同学的思路是:延长DM交EF于点N,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(2)如图,当点B、C、F在一条直线上时,
(1)中的结论还成立吗?如果成立,
请证明;如果不成立,说明理由.
?
?
?
?
?
?
知识点复习
知识点复习
△AMD≌△FMN
AD=FN=DC,DM=NM.
∠2=∠EFC=
45°
EC=EF
△EDC≌△ENF
ED=EN
DM⊥EM
∠3=∠4
∠DEN=90°
解题思路
课堂练习
1.
如图,四边形ABCD是正方形,AE⊥BE于点E,且AE=3,BE=4,则阴影部分的面积是_________________.
?
2.
如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF.
第1题图
第2题图
课堂练习
3.
如图,矩形ABCD
的对角线AC、BD
相交于点O,CE⊥BO
于E,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
4.如图,在菱形
ABCD和菱形BEFG
中,点A、B、E
在同一条直线上,
P是线段DF的中点,连结PG、PC
,若∠ABC=∠BEF=
60°,求证:
.
:
第3题图
第4题图
1.本节课复习了哪些数学知识?
总结反思
2.在解决问题的过程中突出的数学思想方法是什么?
平行四边形的问题往往转化为三角形来解决,同时平行四边形又为三角形全等提供边等和角等.
3.畅所欲言:本节课中你有什么收获?还有什么疑惑呢?
