2020—2021学年人教版数学七年级下册6.3实数课件(共28张)
文档属性
| 名称 | 2020—2021学年人教版数学七年级下册6.3实数课件(共28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
实
数
学习目标
1、理解实数的概念;
2、理解有理数关于相反数和绝对值的意义;
3、能够对所学的数据进行合理分类;
4、能够掌握实数的运算法则及运算性质并进行运算。
重点
难点
重难点
实数的相关概念及运算。
实数的运算。
思考回顾
把有理数
写成小数的形式,它们有什么特征?
发现上面的分数都可以写成有限小数或者无限循环小数的形式。
归纳:任何一个有理数(整数或分数)都可以写成有限小数或者无限循环小数的形式,反过来,任何有限小数或者无限循环小数也都是有理数。
探究新知
1.010
010
001
000
01…
“小数就是有理数”。这样认为对吗?为什么?
无限不循环小数叫做无理数.
小试牛刀
下列各数中,哪些是有理数?哪些是无理数?
5,
3.14,
0,
无理数
通过刚才的结果,你能总结无理数的常见形式?
(1)含
的一些数;
(2)开不尽方的根;
(3)无限不循环的小数;
(4)有理数与无理数的和或差.
实数
1、有理数和无理数统称实数.
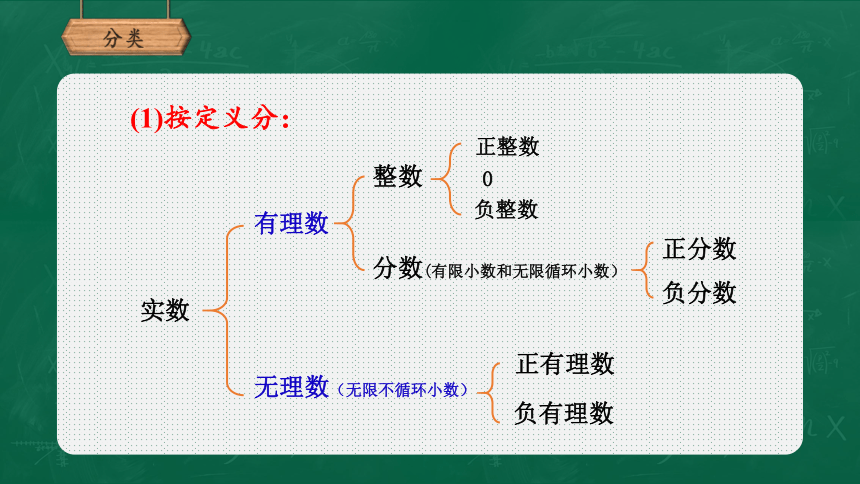
2、我们学过的数可以这样分类.
分类
实数
有理数
无理数(无限不循环小数)
整数
分数(有限小数和无限循环小数)
正整数
负整数
0
正分数
负分数
正有理数
负有理数
(1)按定义分:
分类
(2)按性质分:
实数
正数
负数
正有理数
正整数
负分数
正无理数
负有理数
负无理数
负整数
负分数
0
练一练
1.实数不是有理数就是无理数。(
)
2.无理数都是无限不循环小数。(
)
3.无理数都是无限小数。(
)
4.带根号的数都是无理数。(
)
5.无理数一定都带根号。(
)
6.两个无理数之积不一定是无理数。(
)
7.两个无理数之和一定是无理数。(
)
练一练
把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
活动探究
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形。
1
1
1
1
新知探究
你能在数轴上找到表示
和
的点吗?
数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
实数与数轴上的点是一一对应的关系。
相反数:
实数a的相反数是-a.
你能解答下列问题吗?
若a与b互为相反数,则a+b=0.
0
(1)
的相反数是______,-p
的相反数是______,
0
的相反数是______
;
p
特殊地:0的相反数是0。
新知探究
实数a的绝对值,记为|a|,它是一个非负实数.
几何意义:
|a|表示点a到原点0的距离.
而|
a-b
|表示点a与点b的距离.
代数意义:
一个正实数的绝对值是它本身;
0的绝对值是0;
一个负实数的绝对值是它的相反数.
绝对值:
新知探究
乘积是1的两个数互为倒数.若a与b互为倒数,则ab=1.
如果a≠0,那么它的倒数为
.
在实数范围内,相反数、倒数、绝对值的意义与有理数范围内,相反数、倒数、绝对值的意义完全一样。
的倒数是
,
的倒数是
;
倒数:
新知探究
1、
的绝对值是(
)
C
2、下列说法正确的是(
)
A.
=-3
B.
0的倒数是0
C.
9的平方根是3
D.
-4的相反数是4
D
例1
练习
例2
计算下列各式的值:
(1)
(2)
解:(1)
加法结合律
分配律
(2)
实数运算
先算乘方和开方,
再算乘除,最后算加减.
如果遇到括号,则先进行括号里的运算.
实数的运算顺序
练习
计算(结果保留小数点后两位):
解:(1)
(2)
例3
下列计算正确的是(
)
B
练习
下列计算正确的是(
)
B
基础巩固
2、
的相反数是
,绝对值是
.
3、绝对值等于
的数是
,
的平方是
.
1、正实数的绝对值是
,0的绝对值是
,负实数的绝对值是
.
它本身
它的相反数
4、a、b互为相反数c与d互为倒数,求a+1+b+cd的值
.
0
2
基础巩固
课堂总结
实数的相关概念
实数的运算
知识
考点
实数的运算
实
数
学习目标
1、理解实数的概念;
2、理解有理数关于相反数和绝对值的意义;
3、能够对所学的数据进行合理分类;
4、能够掌握实数的运算法则及运算性质并进行运算。
重点
难点
重难点
实数的相关概念及运算。
实数的运算。
思考回顾
把有理数
写成小数的形式,它们有什么特征?
发现上面的分数都可以写成有限小数或者无限循环小数的形式。
归纳:任何一个有理数(整数或分数)都可以写成有限小数或者无限循环小数的形式,反过来,任何有限小数或者无限循环小数也都是有理数。
探究新知
1.010
010
001
000
01…
“小数就是有理数”。这样认为对吗?为什么?
无限不循环小数叫做无理数.
小试牛刀
下列各数中,哪些是有理数?哪些是无理数?
5,
3.14,
0,
无理数
通过刚才的结果,你能总结无理数的常见形式?
(1)含
的一些数;
(2)开不尽方的根;
(3)无限不循环的小数;
(4)有理数与无理数的和或差.
实数
1、有理数和无理数统称实数.
2、我们学过的数可以这样分类.
分类
实数
有理数
无理数(无限不循环小数)
整数
分数(有限小数和无限循环小数)
正整数
负整数
0
正分数
负分数
正有理数
负有理数
(1)按定义分:
分类
(2)按性质分:
实数
正数
负数
正有理数
正整数
负分数
正无理数
负有理数
负无理数
负整数
负分数
0
练一练
1.实数不是有理数就是无理数。(
)
2.无理数都是无限不循环小数。(
)
3.无理数都是无限小数。(
)
4.带根号的数都是无理数。(
)
5.无理数一定都带根号。(
)
6.两个无理数之积不一定是无理数。(
)
7.两个无理数之和一定是无理数。(
)
练一练
把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
活动探究
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形。
1
1
1
1
新知探究
你能在数轴上找到表示
和
的点吗?
数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
实数与数轴上的点是一一对应的关系。
相反数:
实数a的相反数是-a.
你能解答下列问题吗?
若a与b互为相反数,则a+b=0.
0
(1)
的相反数是______,-p
的相反数是______,
0
的相反数是______
;
p
特殊地:0的相反数是0。
新知探究
实数a的绝对值,记为|a|,它是一个非负实数.
几何意义:
|a|表示点a到原点0的距离.
而|
a-b
|表示点a与点b的距离.
代数意义:
一个正实数的绝对值是它本身;
0的绝对值是0;
一个负实数的绝对值是它的相反数.
绝对值:
新知探究
乘积是1的两个数互为倒数.若a与b互为倒数,则ab=1.
如果a≠0,那么它的倒数为
.
在实数范围内,相反数、倒数、绝对值的意义与有理数范围内,相反数、倒数、绝对值的意义完全一样。
的倒数是
,
的倒数是
;
倒数:
新知探究
1、
的绝对值是(
)
C
2、下列说法正确的是(
)
A.
=-3
B.
0的倒数是0
C.
9的平方根是3
D.
-4的相反数是4
D
例1
练习
例2
计算下列各式的值:
(1)
(2)
解:(1)
加法结合律
分配律
(2)
实数运算
先算乘方和开方,
再算乘除,最后算加减.
如果遇到括号,则先进行括号里的运算.
实数的运算顺序
练习
计算(结果保留小数点后两位):
解:(1)
(2)
例3
下列计算正确的是(
)
B
练习
下列计算正确的是(
)
B
基础巩固
2、
的相反数是
,绝对值是
.
3、绝对值等于
的数是
,
的平方是
.
1、正实数的绝对值是
,0的绝对值是
,负实数的绝对值是
.
它本身
它的相反数
4、a、b互为相反数c与d互为倒数,求a+1+b+cd的值
.
0
2
基础巩固
课堂总结
实数的相关概念
实数的运算
知识
考点
实数的运算
