六年级数学下册课件-7.2立体图形的表面积和体积 -苏教版34页
文档属性
| 名称 | 六年级数学下册课件-7.2立体图形的表面积和体积 -苏教版34页 |  | |
| 格式 | zip | ||
| 文件大小 | 19.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 06:19:33 | ||
图片预览



文档简介
(共34张PPT)
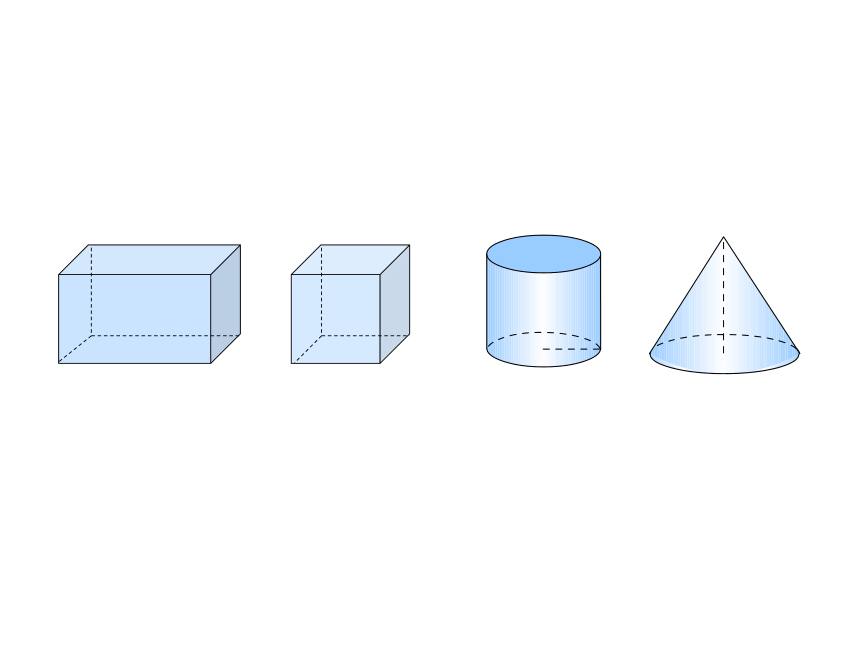
立体图形的表面积和体积
苏教版小学数学六年级下册
什么是立体图形的表面积?
一个立体图形所有面的面积总和,叫做它的表面积。
什么是立体图形的体积?
一个立体图形所占空间的大小,叫做它的体积。
什么叫做容器的容积?
容器所能容纳物体的体积
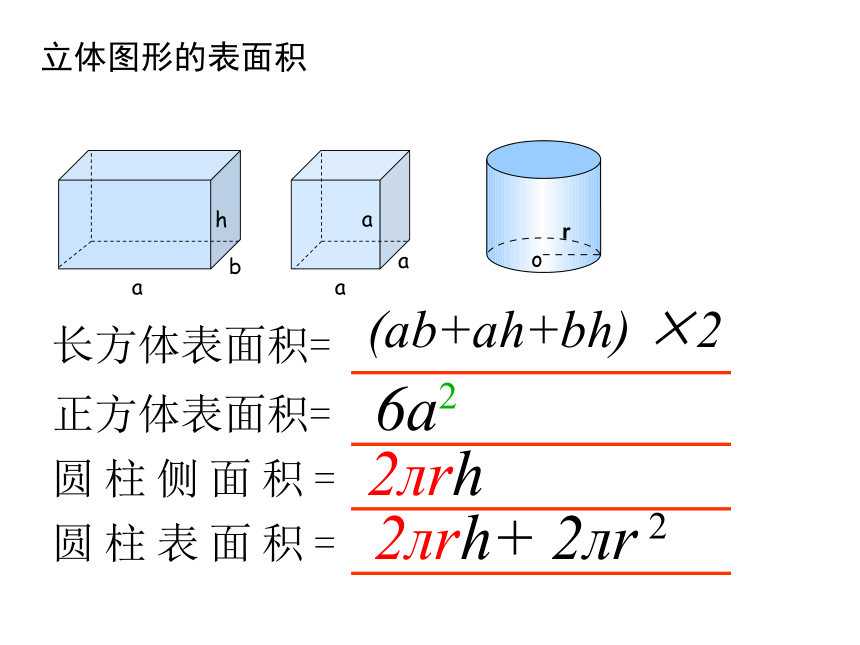
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh)
×2
6a
2лrh
2лrh+
2лr
2
2
a
b
o
r
h
a
a
a
立体图形的表面积
a
b
h
o
r
h
s
a
a
a
h
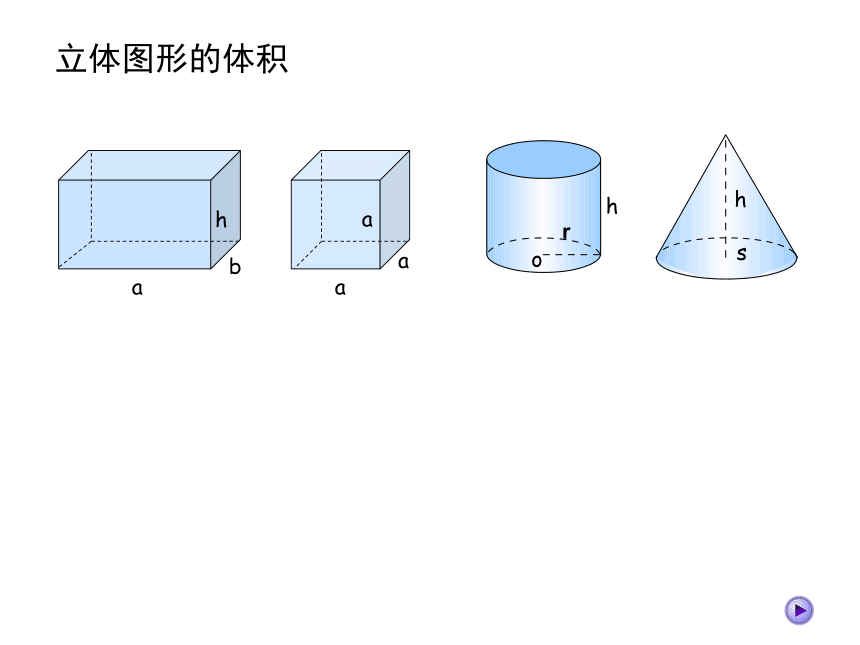
立体图形的体积
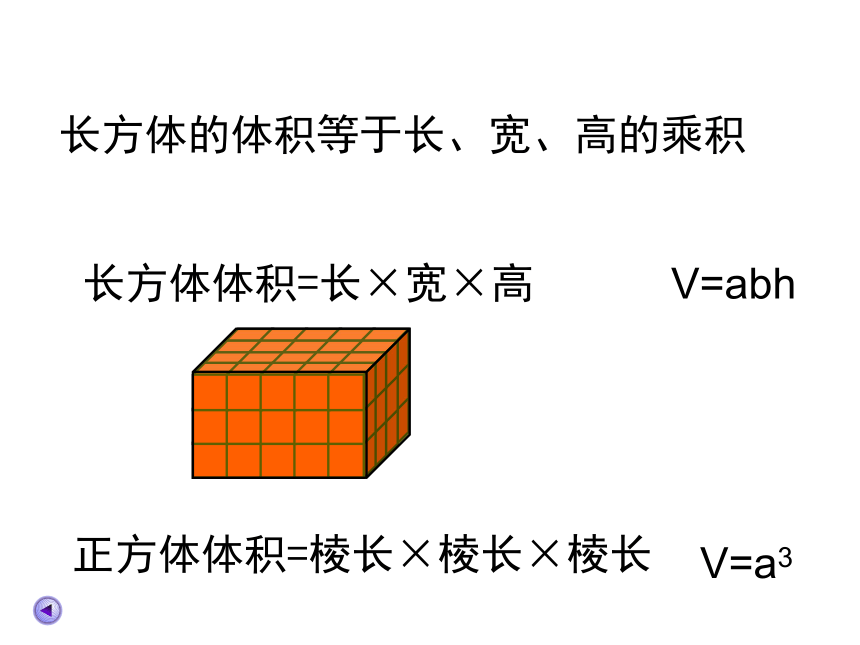
长方体的体积等于长、宽、高的乘积
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
V=a3
a
b
h
o
r
h
s
a
a
a
h
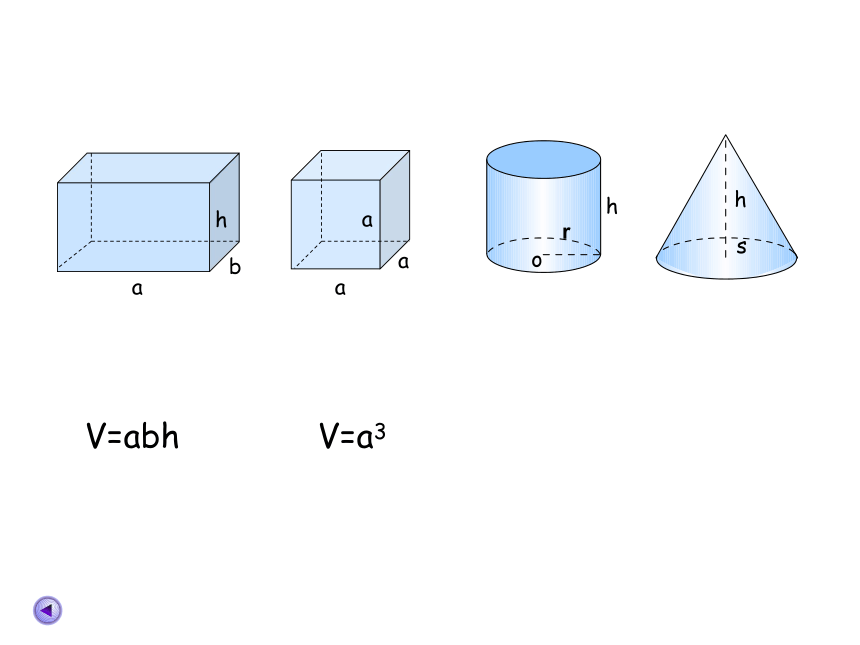
V=abh
V=a3
a
b
h
o
r
h
s
a
a
a
h
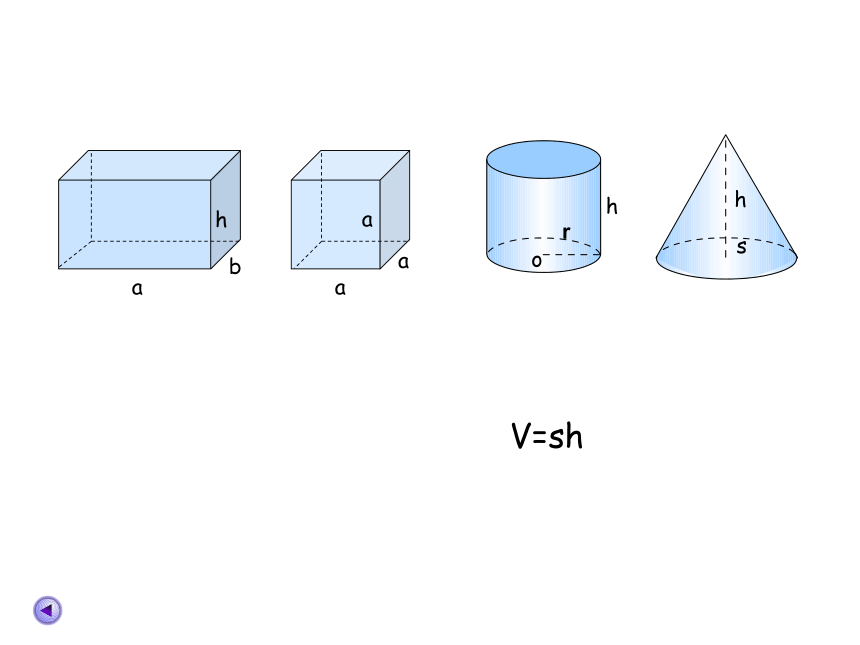
V=sh
长方体的体积=底面积
x
高
底面积
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
高
长方体的体积=底面积
x
高
圆柱体的体积=
x
底面积
a
b
h
o
r
h
s
a
a
a
h
V=
sh
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
a
b
h
o
r
h
s
a
a
a
h
V=abh
V=a3
V=sh
V=
sh
a
b
h
o
r
h
s
a
a
a
h
V=abh
V=a3
V=sh
V=
sh
V=sh
V=
sh
V=abh
2、一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是(
)
A.1:2?
B.2:?
C.1:?
D.?:1
C
1、长方体、正方体、圆柱的底面周长和高都相等,哪个体积最大(
)。
A、长方体
B、正方体
C、圆柱
C
选择题
判断题。
1、把一个圆柱切拼成一个近似的长方体,体积不变,表面积也不变.(
?
)
2、一个圆柱,底面半径扩大2倍,高缩小为原来的
,体积不变.
(
)
3、如果一个圆锥的体积等于一个圆柱体积的
,那么它们一定等底等高.(
)
一个长方体木块的长、宽、高的比是
3:1:1,已知长方体的长是30厘米、这个长方体的体积(
)立方分米,将这个长方体木块削成高是30厘米的最大的圆柱,体积是(
)立方厘米。
3
750?
填空题
一个底面直径为20厘米、高为50厘米的圆木,如果沿着它的底面直径削成两个同样的半圆柱,那么表面积增加(
)平方厘米;如果把它截成3个小圆柱,那么表面积增加(
)平方厘米。
2000
400?
一块边长为12dm的正方形铁皮,四个角分别截掉一个小正方形,剩下的部分恰好能焊成个无盖的正方体容器,这个容器的容积是(
)立方分米。
64
1、一台压路机的前轮宽2米,横截面直径为1.2米,如果每分钟转10圈,那么压路机工作半小时压路的面积是多少平方米?
解决问题
?×1.2×2=(平方米)
2.4?×10×30=720?(平方米)
答:压路机工作半小时压路的面积是720?平方米。
如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
12.56÷3.14÷2
=2(米)
?×22×3×
=4
?(立方米)
750×4?=3000?(千克)=3?(吨)
答:这堆小麦大约重3?吨。
3米
12.56米
3、一根圆柱形的木料,高是10厘米,侧面积是188.4平方厘米.
(1)
它的底面半径是多少厘米?
(2)
把它加工成一个体积最大的圆锥,这个圆锥的体积是多少立方厘米。
188.4÷10=18.84(厘米)
18.84÷3.14÷2=3(厘米)
×?×3×3×10=30?(立方厘米)
答:它的底面半径是3厘米,
这个圆锥的体积是30?立方厘米。
3、一个圆柱和一个圆锥,它们的高相等,体积之比是4:3。圆锥的底面积是36平方分米,圆柱的底面积是(
)平方分米。
A.12
B.24
C.36
D.16
D
这节课你有什么收获?
立体图形的表面积和体积
苏教版小学数学六年级下册
什么是立体图形的表面积?
一个立体图形所有面的面积总和,叫做它的表面积。
什么是立体图形的体积?
一个立体图形所占空间的大小,叫做它的体积。
什么叫做容器的容积?
容器所能容纳物体的体积
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh)
×2
6a
2лrh
2лrh+
2лr
2
2
a
b
o
r
h
a
a
a
立体图形的表面积
a
b
h
o
r
h
s
a
a
a
h
立体图形的体积
长方体的体积等于长、宽、高的乘积
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
V=a3
a
b
h
o
r
h
s
a
a
a
h
V=abh
V=a3
a
b
h
o
r
h
s
a
a
a
h
V=sh
长方体的体积=底面积
x
高
底面积
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
底面积
长方体的体积=底面积
x
高
高
长方体的体积=底面积
x
高
圆柱体的体积=
x
底面积
a
b
h
o
r
h
s
a
a
a
h
V=
sh
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
a
b
h
o
r
h
s
a
a
a
h
V=abh
V=a3
V=sh
V=
sh
a
b
h
o
r
h
s
a
a
a
h
V=abh
V=a3
V=sh
V=
sh
V=sh
V=
sh
V=abh
2、一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是(
)
A.1:2?
B.2:?
C.1:?
D.?:1
C
1、长方体、正方体、圆柱的底面周长和高都相等,哪个体积最大(
)。
A、长方体
B、正方体
C、圆柱
C
选择题
判断题。
1、把一个圆柱切拼成一个近似的长方体,体积不变,表面积也不变.(
?
)
2、一个圆柱,底面半径扩大2倍,高缩小为原来的
,体积不变.
(
)
3、如果一个圆锥的体积等于一个圆柱体积的
,那么它们一定等底等高.(
)
一个长方体木块的长、宽、高的比是
3:1:1,已知长方体的长是30厘米、这个长方体的体积(
)立方分米,将这个长方体木块削成高是30厘米的最大的圆柱,体积是(
)立方厘米。
3
750?
填空题
一个底面直径为20厘米、高为50厘米的圆木,如果沿着它的底面直径削成两个同样的半圆柱,那么表面积增加(
)平方厘米;如果把它截成3个小圆柱,那么表面积增加(
)平方厘米。
2000
400?
一块边长为12dm的正方形铁皮,四个角分别截掉一个小正方形,剩下的部分恰好能焊成个无盖的正方体容器,这个容器的容积是(
)立方分米。
64
1、一台压路机的前轮宽2米,横截面直径为1.2米,如果每分钟转10圈,那么压路机工作半小时压路的面积是多少平方米?
解决问题
?×1.2×2=(平方米)
2.4?×10×30=720?(平方米)
答:压路机工作半小时压路的面积是720?平方米。
如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
12.56÷3.14÷2
=2(米)
?×22×3×
=4
?(立方米)
750×4?=3000?(千克)=3?(吨)
答:这堆小麦大约重3?吨。
3米
12.56米
3、一根圆柱形的木料,高是10厘米,侧面积是188.4平方厘米.
(1)
它的底面半径是多少厘米?
(2)
把它加工成一个体积最大的圆锥,这个圆锥的体积是多少立方厘米。
188.4÷10=18.84(厘米)
18.84÷3.14÷2=3(厘米)
×?×3×3×10=30?(立方厘米)
答:它的底面半径是3厘米,
这个圆锥的体积是30?立方厘米。
3、一个圆柱和一个圆锥,它们的高相等,体积之比是4:3。圆锥的底面积是36平方分米,圆柱的底面积是(
)平方分米。
A.12
B.24
C.36
D.16
D
这节课你有什么收获?
