3.3垂径定理课件(25张)
图片预览




文档简介
3.3 垂径定理
第三章 圆
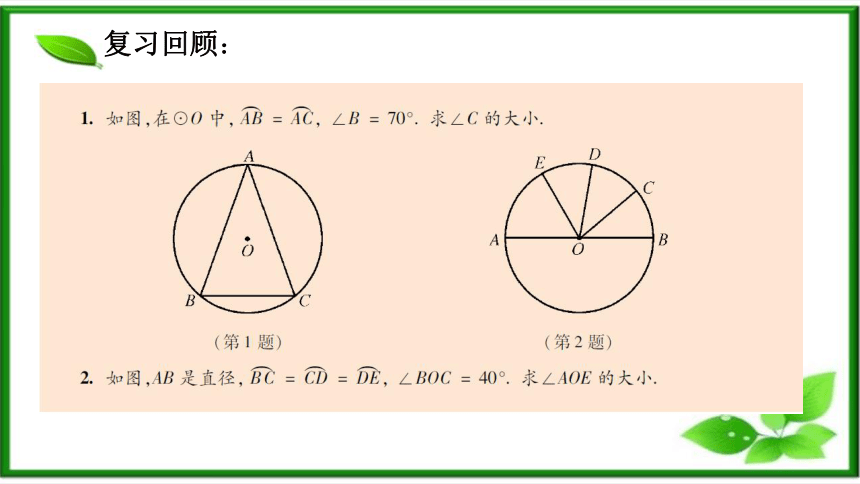
复习回顾:
预习检测
1.如图已知⊙O 的半径为 13 ,弦 AB 长为 24,点 O 到 AB 的距离是( )
A.6 B.5 C.4 D.3
2 .如图AB 是⊙O 的直径, 弦 CD⊥AB 于点 E ,下列结论正确的是( )
︵ ︵
A.OE=BE B.BC=BD
C.△BOC 是等边三角形
D.四边形 ODBC 是菱形
B
B
如图,当AB⊥CD时,图中又有哪些相等的线段和相等的弧?
新课导入
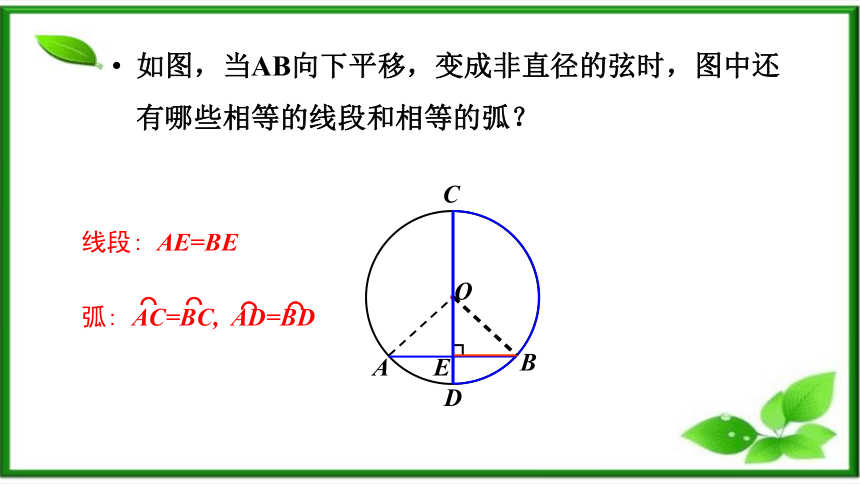
如图,当AB向下平移,变成非直径的弦时,图中还有哪些相等的线段和相等的弧?
·
O
A
B
D
E
C
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
垂径定理
·
O
A
B
C
D
E
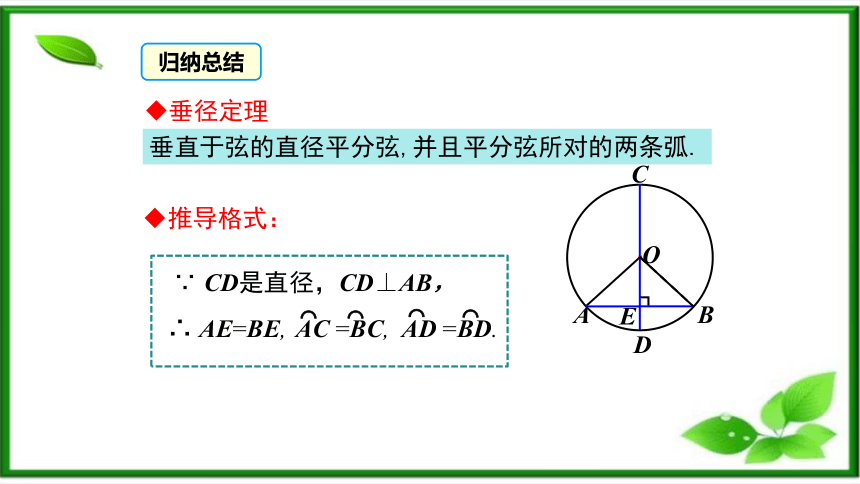
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
归纳总结
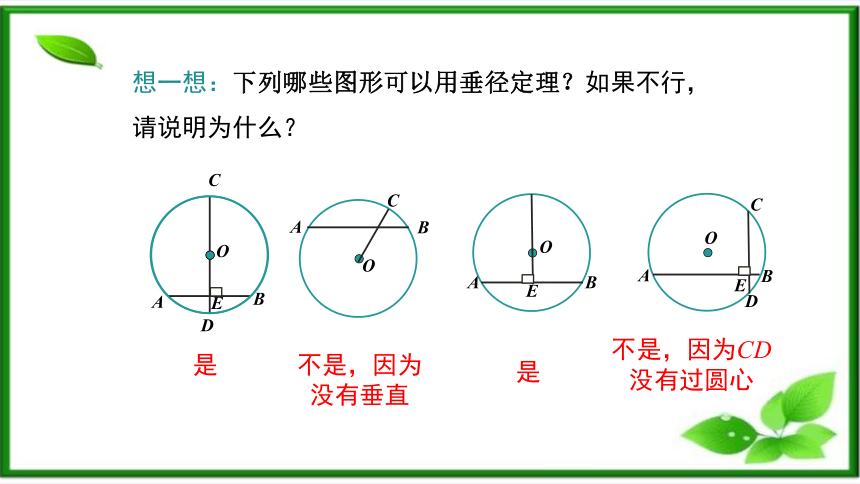
想一想:下列哪些图形可以用垂径定理?如果不行,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
C
归纳总结
A
B
O
D
C
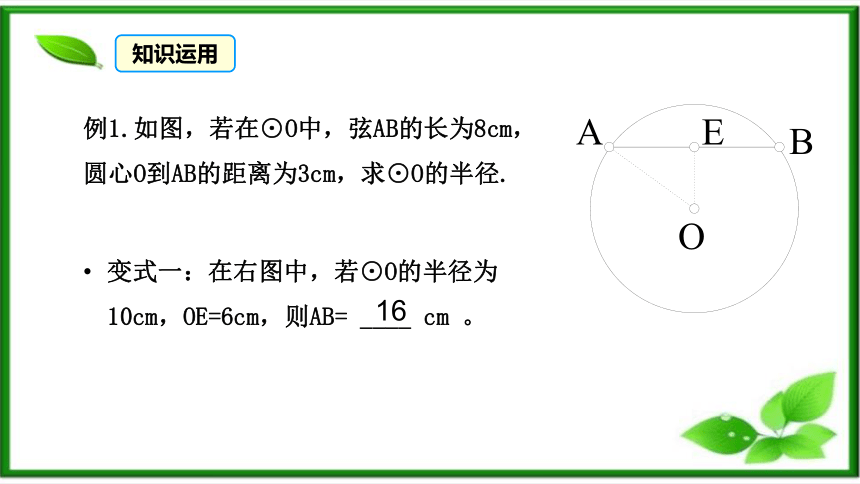
例1.如图,若在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.
变式一:在右图中,若⊙O的半径为10cm,OE=6cm,则AB= ____ cm 。
知识运用
16
变式二: 如图3,在⊙O中,半径OC⊥AB,垂足为E,若CE=2cm,AB=8cm,则⊙O的半径____cm 。
2
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
·
O
A
B
C
D
E
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
(2)由垂径定理可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
推论1
⌒
⌒
⌒
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论1
·
O
A
B
C
D
归纳总结
试一试:根据刚刚所学,你能利用垂径定理求出引入中赵州桥主桥拱半径的问题吗?它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.23m,你能算出桥拱所在圆的半径吗?
垂径定理的实际应用
三
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
∴ AB=37m,CD=7.23m.
解得R≈27.3(m).
即主桥拱半径约为27.3m.
=18.52+(R-7.23)2
∴ AD= AB=18.5m,
OD=OC-CD=R-7.23.
弦a,弦心距d,弓形高h,半径r之间有以下关系:
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
归纳总结
1.如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
A.5cm B.25cm C.2cm D.1cm.
当堂练习
C
2.已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
4
4有一石拱桥的桥拱是圆弧形,如下图所示,正常水位下水面宽AB=60米,水面到拱顶距离CD=18米,当洪水泛滥,水面宽MN=32米时是否需要采取紧急措施?请说明理由(当水面距拱顶3米以内时需采取紧急措施).
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
课堂小结
拓展提升:
如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,那么OP长的取值范围 .
3cm≤OP≤5cm
B
A
O
P
第三章 圆
复习回顾:
预习检测
1.如图已知⊙O 的半径为 13 ,弦 AB 长为 24,点 O 到 AB 的距离是( )
A.6 B.5 C.4 D.3
2 .如图AB 是⊙O 的直径, 弦 CD⊥AB 于点 E ,下列结论正确的是( )
︵ ︵
A.OE=BE B.BC=BD
C.△BOC 是等边三角形
D.四边形 ODBC 是菱形
B
B
如图,当AB⊥CD时,图中又有哪些相等的线段和相等的弧?
新课导入
如图,当AB向下平移,变成非直径的弦时,图中还有哪些相等的线段和相等的弧?
·
O
A
B
D
E
C
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
垂径定理
·
O
A
B
C
D
E
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
归纳总结
想一想:下列哪些图形可以用垂径定理?如果不行,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
C
归纳总结
A
B
O
D
C
例1.如图,若在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.
变式一:在右图中,若⊙O的半径为10cm,OE=6cm,则AB= ____ cm 。
知识运用
16
变式二: 如图3,在⊙O中,半径OC⊥AB,垂足为E,若CE=2cm,AB=8cm,则⊙O的半径____cm 。
2
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
·
O
A
B
C
D
E
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
(2)由垂径定理可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
推论1
⌒
⌒
⌒
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论1
·
O
A
B
C
D
归纳总结
试一试:根据刚刚所学,你能利用垂径定理求出引入中赵州桥主桥拱半径的问题吗?它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.23m,你能算出桥拱所在圆的半径吗?
垂径定理的实际应用
三
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
∴ AB=37m,CD=7.23m.
解得R≈27.3(m).
即主桥拱半径约为27.3m.
=18.52+(R-7.23)2
∴ AD= AB=18.5m,
OD=OC-CD=R-7.23.
弦a,弦心距d,弓形高h,半径r之间有以下关系:
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
归纳总结
1.如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
A.5cm B.25cm C.2cm D.1cm.
当堂练习
C
2.已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
4
4有一石拱桥的桥拱是圆弧形,如下图所示,正常水位下水面宽AB=60米,水面到拱顶距离CD=18米,当洪水泛滥,水面宽MN=32米时是否需要采取紧急措施?请说明理由(当水面距拱顶3米以内时需采取紧急措施).
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
课堂小结
拓展提升:
如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,那么OP长的取值范围 .
3cm≤OP≤5cm
B
A
O
P
