3.2 第1课时 旋转的定义与性质课件(20张)
文档属性
| 名称 | 3.2 第1课时 旋转的定义与性质课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 20:39:26 | ||
图片预览







文档简介
第三章 图形的平移与旋转
2 第1课时 旋转的定义与性质
课堂小结
例题讲解
情景导入
随堂演练
获取新知
情景导入
(1)上面场景中的转动现象,有什么共同特征?
(2)风力发电机的叶片、钟表的指针在转动过程中,其形状、大小、位置是否发生改变?
获取新知
问题 观察下列图形的运动,它有什么特点?
B
O
A
45
0
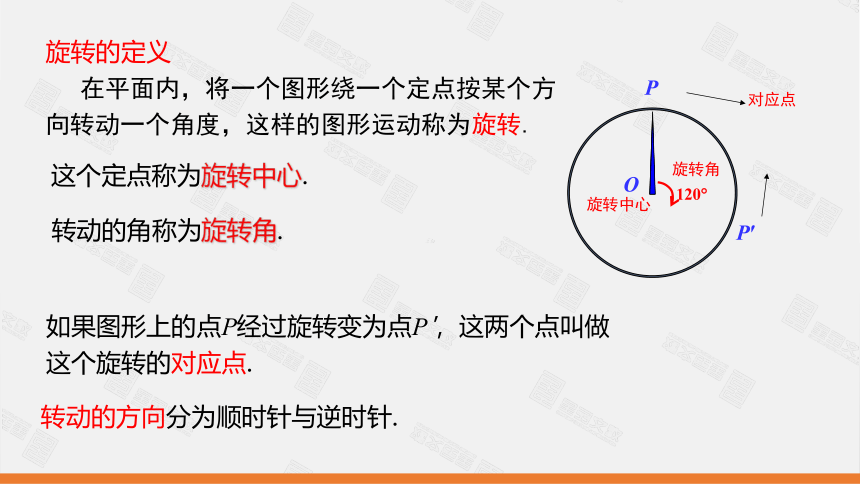
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
O
P′
P
旋转中心
旋转角
对应点
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
旋转与平移类似,也属于全等变换,即运动前后改变的是图形的位置,图形的形状和大小都不变
A
B
C
D
E
F
O
如图,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,点A,B,C分别旋转到了点D,E,F.点A与点D是一组对应点,线段AB与线段DE是一组对应线段,∠BAC与∠EDF是一组对应角.在这一旋转过程中,点O是旋转中心, ∠AOD,∠BOE,∠COF都是旋转角.
做一做:
如图,两张透明纸上的四边形ABCD和四边形EFGH完全重合,在纸上选取旋转中心O,并将其固定.把其中一张纸片绕点O旋转一定角度.
A(E)
B(F)
D(H)
C(G)
B
C
D
H
E
F
G
A
O
(1)观察图中的两个四边形,你能发现有哪些相等的线段和相等的角?
AB=EF,BC=FG,CD=GH,DA=HE.
∠A=∠E,∠B=∠F,∠C=∠G , ∠D=∠H.
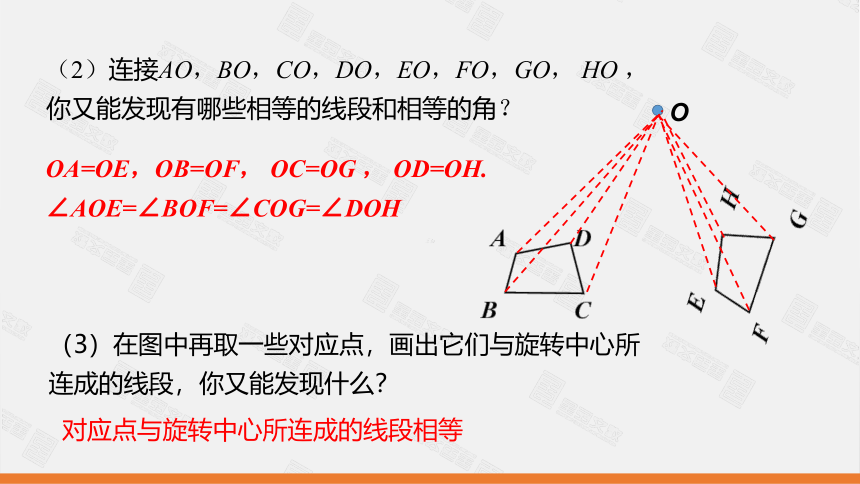
(2)连接AO,BO,CO,DO,EO,FO,GO, HO ,你又能发现有哪些相等的线段和相等的角?
O
OA=OE,OB=OF, OC=OG , OD=OH.
∠AOE=∠BOF=∠COG=∠DOH
(3)在图中再取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么?
对应点与旋转中心所连成的线段相等
1.对应点到旋转中心的距离相等;
2.任意一组对应点与旋转中心的连线所成的角都等于旋转角;
3.对应线段相等,对应角相等.
旋转的性质
例题讲解
例1 如图所示,△ABC是直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是______;旋转的角度是____;AC的对应边是____;∠A的对应角是________;点C的对应点是______.
点B
90°
ED
∠BED
点D
例2 如图,在正方形ABCD中,点E在BC上,△DEC按 顺时针方向旋转一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?旋转角度是多少?
(2)指明图中旋转图形的对应线段与对应角.
(3)图中有除正方形的四边相等、四角相等外的相等线段与相等角吗?有没有能够完全重合的两个三角形?若有,请各找出一对;若没有,说明理由.
根据图形旋转的性质可以得到:
(1) △DEC是绕点D顺时针旋转90°后到达△DGA位置的,所以点D为旋转中心,旋转角度是90°.
(2) DE与DG,DC与DA,EC与GA是对应线段, ∠CDE与∠ADG,∠C与∠DAG,∠DEC与∠G是对应角.
(3)有.相等线段有:DG=DE(答案不唯一);
相等角有:∠G=∠DEC(答案不唯一);
能够完全重合的两个三角形是△DEC与△DGA.
随堂演练
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
2. 如图,△ABC按顺时针方向旋转到△ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
C
4. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,
∠BAC=130°,则AD= = cm, DE= = cm,
∠EAC=∠ = °.
AB
5
BC
8
BAD
30
5. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= ________.
80或120
6. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B两点不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.
(1)证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE.(2)∵∠ACB=90°,AC=BC,
∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠CBE=∠A=45°,AD=BE.
∵AD=BF,∴BE=BF,
∴∠BEF= ×(180°-45°)=67.5°.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角
2 第1课时 旋转的定义与性质
课堂小结
例题讲解
情景导入
随堂演练
获取新知
情景导入
(1)上面场景中的转动现象,有什么共同特征?
(2)风力发电机的叶片、钟表的指针在转动过程中,其形状、大小、位置是否发生改变?
获取新知
问题 观察下列图形的运动,它有什么特点?
B
O
A
45
0
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
O
P′
P
旋转中心
旋转角
对应点
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
旋转与平移类似,也属于全等变换,即运动前后改变的是图形的位置,图形的形状和大小都不变
A
B
C
D
E
F
O
如图,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,点A,B,C分别旋转到了点D,E,F.点A与点D是一组对应点,线段AB与线段DE是一组对应线段,∠BAC与∠EDF是一组对应角.在这一旋转过程中,点O是旋转中心, ∠AOD,∠BOE,∠COF都是旋转角.
做一做:
如图,两张透明纸上的四边形ABCD和四边形EFGH完全重合,在纸上选取旋转中心O,并将其固定.把其中一张纸片绕点O旋转一定角度.
A(E)
B(F)
D(H)
C(G)
B
C
D
H
E
F
G
A
O
(1)观察图中的两个四边形,你能发现有哪些相等的线段和相等的角?
AB=EF,BC=FG,CD=GH,DA=HE.
∠A=∠E,∠B=∠F,∠C=∠G , ∠D=∠H.
(2)连接AO,BO,CO,DO,EO,FO,GO, HO ,你又能发现有哪些相等的线段和相等的角?
O
OA=OE,OB=OF, OC=OG , OD=OH.
∠AOE=∠BOF=∠COG=∠DOH
(3)在图中再取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么?
对应点与旋转中心所连成的线段相等
1.对应点到旋转中心的距离相等;
2.任意一组对应点与旋转中心的连线所成的角都等于旋转角;
3.对应线段相等,对应角相等.
旋转的性质
例题讲解
例1 如图所示,△ABC是直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是______;旋转的角度是____;AC的对应边是____;∠A的对应角是________;点C的对应点是______.
点B
90°
ED
∠BED
点D
例2 如图,在正方形ABCD中,点E在BC上,△DEC按 顺时针方向旋转一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?旋转角度是多少?
(2)指明图中旋转图形的对应线段与对应角.
(3)图中有除正方形的四边相等、四角相等外的相等线段与相等角吗?有没有能够完全重合的两个三角形?若有,请各找出一对;若没有,说明理由.
根据图形旋转的性质可以得到:
(1) △DEC是绕点D顺时针旋转90°后到达△DGA位置的,所以点D为旋转中心,旋转角度是90°.
(2) DE与DG,DC与DA,EC与GA是对应线段, ∠CDE与∠ADG,∠C与∠DAG,∠DEC与∠G是对应角.
(3)有.相等线段有:DG=DE(答案不唯一);
相等角有:∠G=∠DEC(答案不唯一);
能够完全重合的两个三角形是△DEC与△DGA.
随堂演练
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
2. 如图,△ABC按顺时针方向旋转到△ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
C
4. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,
∠BAC=130°,则AD= = cm, DE= = cm,
∠EAC=∠ = °.
AB
5
BC
8
BAD
30
5. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= ________.
80或120
6. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B两点不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.
(1)证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE.(2)∵∠ACB=90°,AC=BC,
∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠CBE=∠A=45°,AD=BE.
∵AD=BF,∴BE=BF,
∴∠BEF= ×(180°-45°)=67.5°.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
