3.8圆内接正多边形课件(14张)
文档属性
| 名称 | 3.8圆内接正多边形课件(14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 253.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览



文档简介
3.8圆内接正多边形
【学习目标】1.让学生了解正多边形、正多边形的内接圆、外接圆以及相关相关概念.2. 了解圆内接正多边形的概念.3. 会用尺规作圆的内接正方形和正六边形.【重难点预测】重点:正多边形、正多边形的内接圆、外接圆以及相关相关概念.难点:正多边形及其边心距、中心角、面积的求法.
一、新课导入
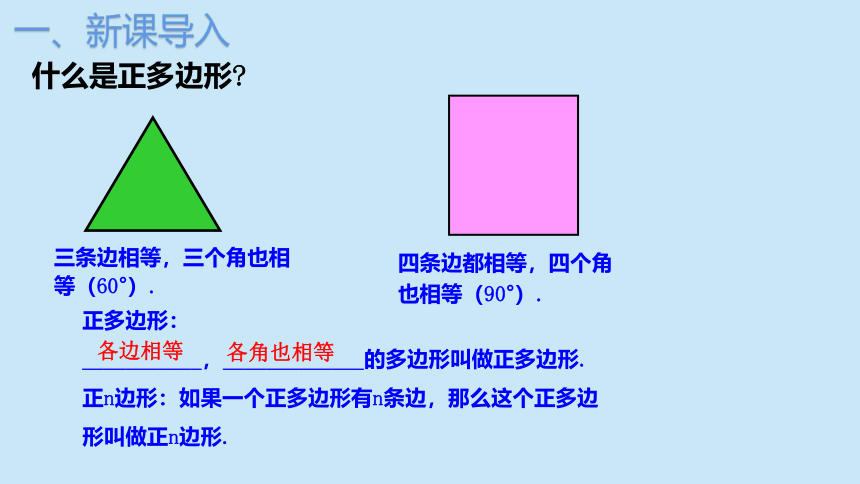
正多边形:
___________,_____________的多边形叫做正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
三条边相等,三个角也相 等(60°).
四条边都相等,四个角也相等(90°).
各边相等
各角也相等
什么是正多边形?
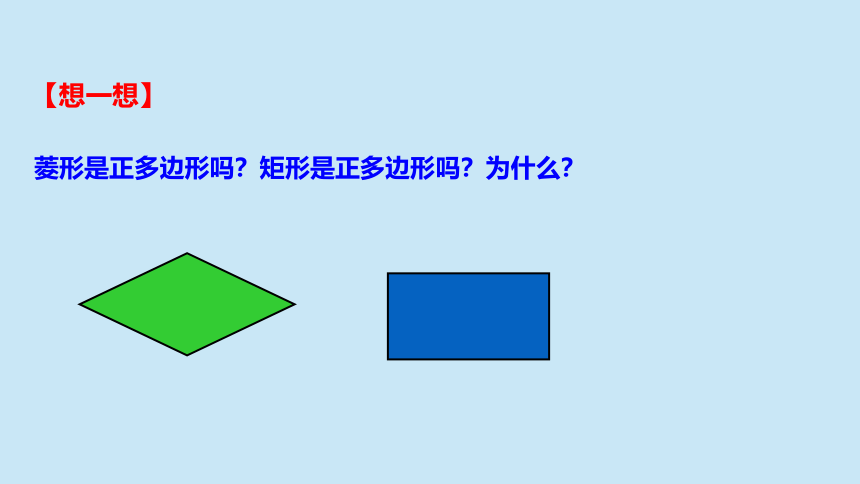
菱形是正多边形吗?矩形是正多边形吗?为什么?
【想一想】
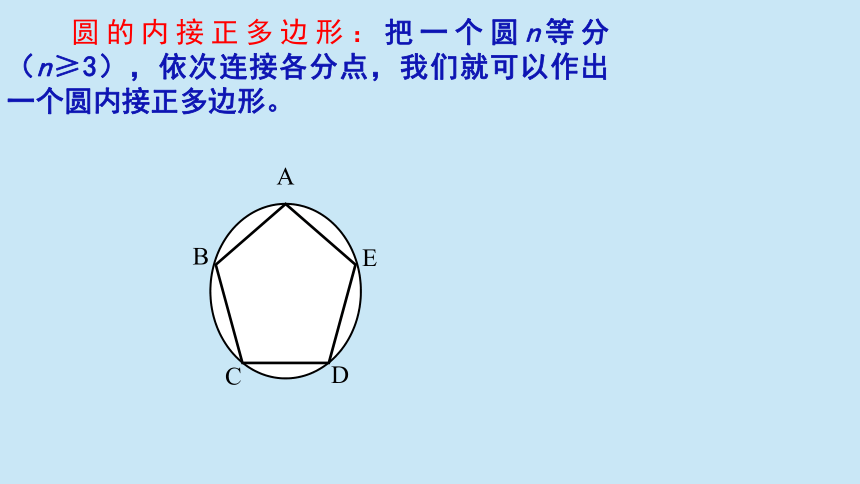
圆的内接正多边形:把一个圆n等分(n≥3),依次连接各分点,我们就可以作出一个圆内接正多边形。
A
B
C
D
E
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
概念解析:
E
C
D
F
.
.
O
A
B
M
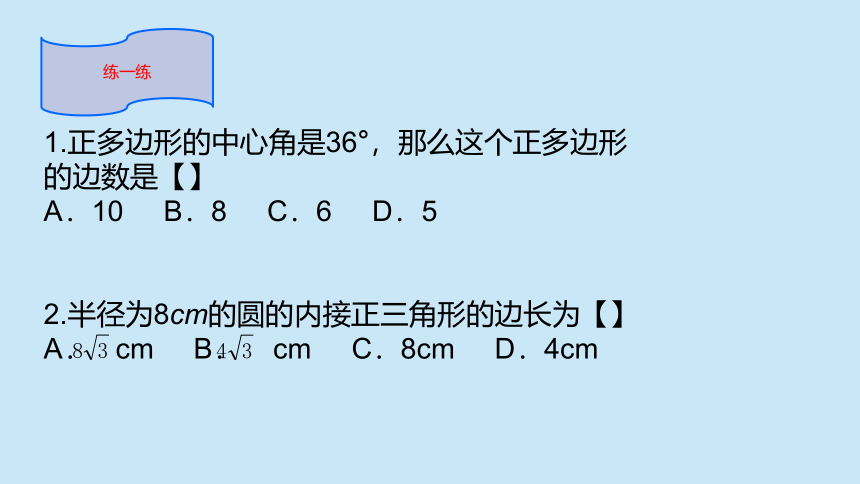
1.正多边形的中心角是36°,那么这个正多边形的边数是【】
A.10 B.8 C.6 D.5
2.半径为8cm的圆的内接正三角形的边长为【】
A. cm B. cm C.8cm D.4cm
练一练
例1:如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC ,垂足为点G,求正六边形的中心角、边长和边心距。
E
F
C
D
.
O
A
B
G
解:连接 OA、OB
∵六边形ABCDEF为正六边形
∴ ∠AOB= =60°
又∵OA=OB
∴ △AOB为等边三角形
∴ AB=OA=OB=OC=4
∵OG⊥BC
在Rt△AOG中,OA=4,AG=2
∴ OG=
∴正六边形ABCDE的中心角为60°,
边长为4,边心距为 。
4.正多边形的有关计算
{5940675A-B579-460E-94D1-54222C63F5DA}正多边形
名称
公式
中心角
正n边形的每个中心角
周长
正n边形的周长
面积
正n边形的面积
补充: 举例:
正n边形的内角和: 正六边形的内角和:______________ 正n边形的内角: 正六边形的内角:______________ 正n边形的外角和: 正六边形的外角和:_____________ 正n边形的外角: 正六边形的外角:______________
例题:正六边形的边长是2,则它的面积是 。
四、巩固练习
1. 如图,五边形ABCDE是⊙O的内接正五边形,圆心O叫做正五边形的 中心;OB是正五边形的半径;∠BOC是这个正五边形的 ;OM⊥BC,垂足为M,OM是这个正五边形的 。
2.有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积.(结果保留根号)
3.分别求出半径为6的圆内接正三角形的边长、边心距和面积.
解:过A作BC边上的高AD,垂足为D
连接OB,则OB=6,
在Rt△OBD中,∠OBD=30°,OB=6,
A
B
C
D
·
O
五、课堂小结
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
A
B
M
【学习目标】1.让学生了解正多边形、正多边形的内接圆、外接圆以及相关相关概念.2. 了解圆内接正多边形的概念.3. 会用尺规作圆的内接正方形和正六边形.【重难点预测】重点:正多边形、正多边形的内接圆、外接圆以及相关相关概念.难点:正多边形及其边心距、中心角、面积的求法.
一、新课导入
正多边形:
___________,_____________的多边形叫做正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
三条边相等,三个角也相 等(60°).
四条边都相等,四个角也相等(90°).
各边相等
各角也相等
什么是正多边形?
菱形是正多边形吗?矩形是正多边形吗?为什么?
【想一想】
圆的内接正多边形:把一个圆n等分(n≥3),依次连接各分点,我们就可以作出一个圆内接正多边形。
A
B
C
D
E
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
概念解析:
E
C
D
F
.
.
O
A
B
M
1.正多边形的中心角是36°,那么这个正多边形的边数是【】
A.10 B.8 C.6 D.5
2.半径为8cm的圆的内接正三角形的边长为【】
A. cm B. cm C.8cm D.4cm
练一练
例1:如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC ,垂足为点G,求正六边形的中心角、边长和边心距。
E
F
C
D
.
O
A
B
G
解:连接 OA、OB
∵六边形ABCDEF为正六边形
∴ ∠AOB= =60°
又∵OA=OB
∴ △AOB为等边三角形
∴ AB=OA=OB=OC=4
∵OG⊥BC
在Rt△AOG中,OA=4,AG=2
∴ OG=
∴正六边形ABCDE的中心角为60°,
边长为4,边心距为 。
4.正多边形的有关计算
{5940675A-B579-460E-94D1-54222C63F5DA}正多边形
名称
公式
中心角
正n边形的每个中心角
周长
正n边形的周长
面积
正n边形的面积
补充: 举例:
正n边形的内角和: 正六边形的内角和:______________ 正n边形的内角: 正六边形的内角:______________ 正n边形的外角和: 正六边形的外角和:_____________ 正n边形的外角: 正六边形的外角:______________
例题:正六边形的边长是2,则它的面积是 。
四、巩固练习
1. 如图,五边形ABCDE是⊙O的内接正五边形,圆心O叫做正五边形的 中心;OB是正五边形的半径;∠BOC是这个正五边形的 ;OM⊥BC,垂足为M,OM是这个正五边形的 。
2.有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积.(结果保留根号)
3.分别求出半径为6的圆内接正三角形的边长、边心距和面积.
解:过A作BC边上的高AD,垂足为D
连接OB,则OB=6,
在Rt△OBD中,∠OBD=30°,OB=6,
A
B
C
D
·
O
五、课堂小结
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
A
B
M
