3.4 圆周角和圆心角的关系课件(25张)
文档属性
| 名称 | 3.4 圆周角和圆心角的关系课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 295.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 20:58:06 | ||
图片预览





文档简介
3.4 圆周角和圆心角的关系
九年级数学下(BS)
教学课件
第三章 圆
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
学习目标
二、预习检测
1.圆周角的概念
角的顶点在圆上,其两边与圆分别还有另一个交点,像这样的角,叫做圆周角
2.圆周角和圆心角的区别和联系
(1)角的顶点的位置不同,圆心角的顶点在圆心处,而圆周角的顶点在圆上.
(2)圆周角和圆心角都对着一条弦,一条弧.
(3)在同一个圆中,一条弧所对的圆心角是惟一的,而它所对的圆周角却有无数个
3.圆周角定理
圆周角的度数等于它所对弧上的圆心角度度数的______
如右下图,用符号语言表示定理为:
在⊙O中,∠ACB=_____∠AOB.
一半
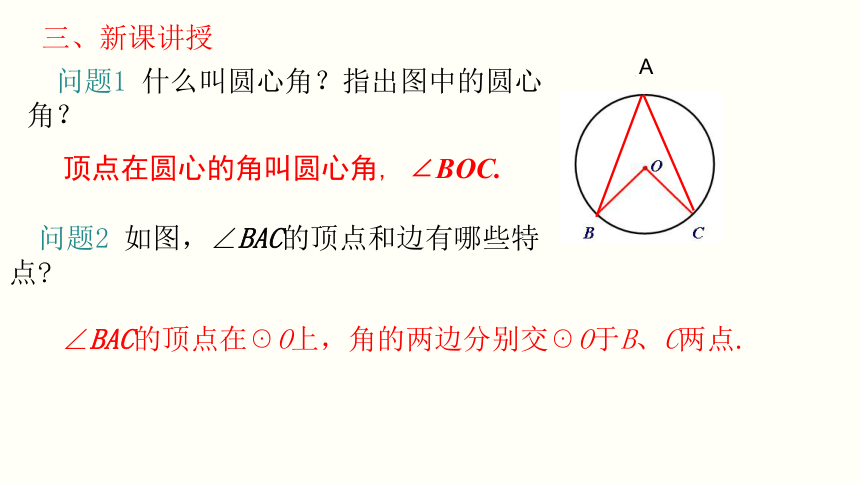
问题1 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图,∠BAC的顶点和边有哪些特点?
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
三、新课讲授
A
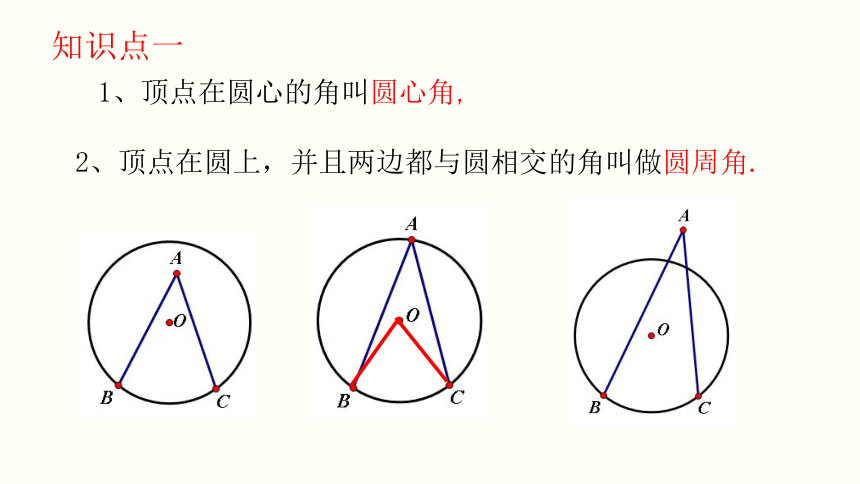
2、顶点在圆上,并且两边都与圆相交的角叫做圆周角.
知识点一
1、顶点在圆心的角叫圆心角,
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
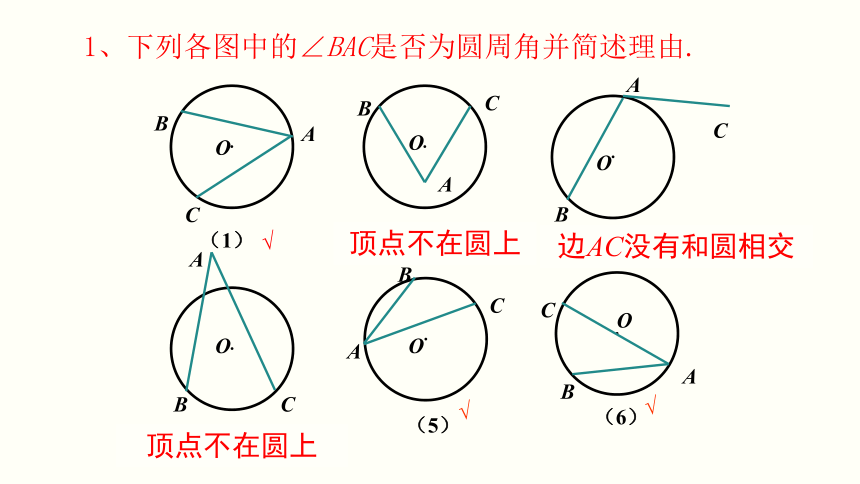
1、下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
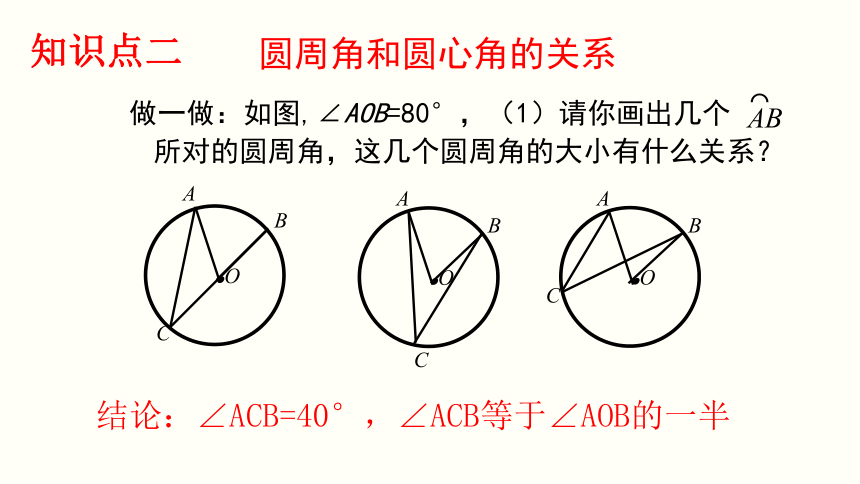
圆周角和圆心角的关系
做一做:如图,∠AOB=80°,(1)请你画出几个 所对的圆周角,这几个圆周角的大小有什么关系?
●O
A
B
●O
A
C
B
●O
A
C
B
C
AB
⌒
知识点二
结论:∠ACB=40°,∠ACB等于∠AOB的一半
推论:
一条弧所对的圆周角等于它所对的圆心角的一半
●O
A
C
B
●O
A
C
B
●O
A
C
B
下面对推论进行演绎证明
1.当圆心(O)在圆周角(∠ACB)的一边(BC)上时,圆周角∠ACB与圆心角∠AOB的大小关系.
∵∠AOB是△ACO的外角,
∴∠AOB=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠C= ∠AOB.
A
C
B
●O
2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?
老师提示:能否转化为1的情况?
过点C作直径CD.由1可得:
D
●O
A
C
B
3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?
老师提示:能否也转化为1的情况?
过点C作直径CD.由1可得:
D
A
C
B
●O
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
A1
A2
A3
推论1:
同弧所对的圆周角相等.
知识点二:
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35?.
(1)∠BOC= ?,
理由是 ;
(2)∠BDC= ?,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
练一练
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
(2)若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
推论2:等弧所对的圆周角相等
知识点三:
如图,四边形ABCD的四个顶点都在☉O上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆。
(1)完成下列填空:
∠1= .
∠2= .
∠3= .
∠5= .
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
∴∠1+∠2+ ∠5+ ∠6=?
∠3+∠4+ ∠7+ ∠8=?
∠1+∠2+ ∠5+ ∠6=180°
∠3+∠4+ ∠7+ ∠8=180°
即:∠BAD+∠BCD=180,
∠ABC+∠ADC=180,
推论:圆内接四边形的对角互补。
例1.如图,已知圆心角∠AOB=100°,则圆周角∠ADB= ,∠ACB= .
D
A
O
C
B
130°
50°
知识点四:
如图,BC是直径,它所对的圆周角有什么特点?如何证明?
推论:直径所对的圆周角是直角,90°的圆周角所对的弦是直径
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
四、随堂练习
2.已知△ABC的三个顶点在⊙O上∠BAC=50°,∠ABC=47°,
则∠AOB= .
B
A
C
O
166°
如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E,(1)BD与CD的大小有什么关系?为什么?
(2)求证: .
A
B
C
D
E
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC, ∴BD=CD.
∵AD平分顶角∠BAC,即∠BAD=∠CAD,
(同圆或等圆中相等的圆周角所对弧相等).
解:BD=CD.理由是:连接AD,
中考链接
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
课堂小结
九年级数学下(BS)
教学课件
第三章 圆
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
学习目标
二、预习检测
1.圆周角的概念
角的顶点在圆上,其两边与圆分别还有另一个交点,像这样的角,叫做圆周角
2.圆周角和圆心角的区别和联系
(1)角的顶点的位置不同,圆心角的顶点在圆心处,而圆周角的顶点在圆上.
(2)圆周角和圆心角都对着一条弦,一条弧.
(3)在同一个圆中,一条弧所对的圆心角是惟一的,而它所对的圆周角却有无数个
3.圆周角定理
圆周角的度数等于它所对弧上的圆心角度度数的______
如右下图,用符号语言表示定理为:
在⊙O中,∠ACB=_____∠AOB.
一半
问题1 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图,∠BAC的顶点和边有哪些特点?
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
三、新课讲授
A
2、顶点在圆上,并且两边都与圆相交的角叫做圆周角.
知识点一
1、顶点在圆心的角叫圆心角,
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
1、下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
圆周角和圆心角的关系
做一做:如图,∠AOB=80°,(1)请你画出几个 所对的圆周角,这几个圆周角的大小有什么关系?
●O
A
B
●O
A
C
B
●O
A
C
B
C
AB
⌒
知识点二
结论:∠ACB=40°,∠ACB等于∠AOB的一半
推论:
一条弧所对的圆周角等于它所对的圆心角的一半
●O
A
C
B
●O
A
C
B
●O
A
C
B
下面对推论进行演绎证明
1.当圆心(O)在圆周角(∠ACB)的一边(BC)上时,圆周角∠ACB与圆心角∠AOB的大小关系.
∵∠AOB是△ACO的外角,
∴∠AOB=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠C= ∠AOB.
A
C
B
●O
2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?
老师提示:能否转化为1的情况?
过点C作直径CD.由1可得:
D
●O
A
C
B
3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?
老师提示:能否也转化为1的情况?
过点C作直径CD.由1可得:
D
A
C
B
●O
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
A1
A2
A3
推论1:
同弧所对的圆周角相等.
知识点二:
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35?.
(1)∠BOC= ?,
理由是 ;
(2)∠BDC= ?,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
练一练
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
(2)若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
推论2:等弧所对的圆周角相等
知识点三:
如图,四边形ABCD的四个顶点都在☉O上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆。
(1)完成下列填空:
∠1= .
∠2= .
∠3= .
∠5= .
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
∴∠1+∠2+ ∠5+ ∠6=?
∠3+∠4+ ∠7+ ∠8=?
∠1+∠2+ ∠5+ ∠6=180°
∠3+∠4+ ∠7+ ∠8=180°
即:∠BAD+∠BCD=180,
∠ABC+∠ADC=180,
推论:圆内接四边形的对角互补。
例1.如图,已知圆心角∠AOB=100°,则圆周角∠ADB= ,∠ACB= .
D
A
O
C
B
130°
50°
知识点四:
如图,BC是直径,它所对的圆周角有什么特点?如何证明?
推论:直径所对的圆周角是直角,90°的圆周角所对的弦是直径
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
四、随堂练习
2.已知△ABC的三个顶点在⊙O上∠BAC=50°,∠ABC=47°,
则∠AOB= .
B
A
C
O
166°
如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E,(1)BD与CD的大小有什么关系?为什么?
(2)求证: .
A
B
C
D
E
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC, ∴BD=CD.
∵AD平分顶角∠BAC,即∠BAD=∠CAD,
(同圆或等圆中相等的圆周角所对弧相等).
解:BD=CD.理由是:连接AD,
中考链接
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
课堂小结
