18.2.1矩形的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 18.2.1矩形的判定 同步练习(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 122.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览

文档简介
18.2.1矩形的判定同步练习
选择题
如图,要使平行四边形ABCD成为矩形,需要添加的条件是()
∠A+∠B=1800 B. ∠B+∠C=1800 C. ∠A=∠B D. ∠B=∠D
平行四边形ABCD中,AC,BD是对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()
AB=BC B. AC=BD C. AC⊥BD D. AB⊥BD
下列关于矩形的说法中正确的是()
对角线相等的四边形是矩形
矩形的对角线相等且互相平分
对角线互相平分的四边形是矩形
矩形的对角线互相垂直且平分
检查一个门框是否为矩形,下列说法中正确的是()
测量两条对角线,是否相等
测量两条对角线,是否互相平分
测量门框的三个角,是否都是直角
测量两条对角线,是否互相垂直
如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()
AB=CD B. AD=BC C. AB=BC D. AC=BD
如图,要使平行四边形ABCD成为矩形,需添加的条件是()
AB=BD B. AC⊥BD C. ∠ABC=∠BAD D. ∠1=∠3
如图,四边形ABCD为平行四边形,延长AD至点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是()
AB=BE B. BE⊥DC C. ∠ADB=900 D.CE⊥DE
填空题
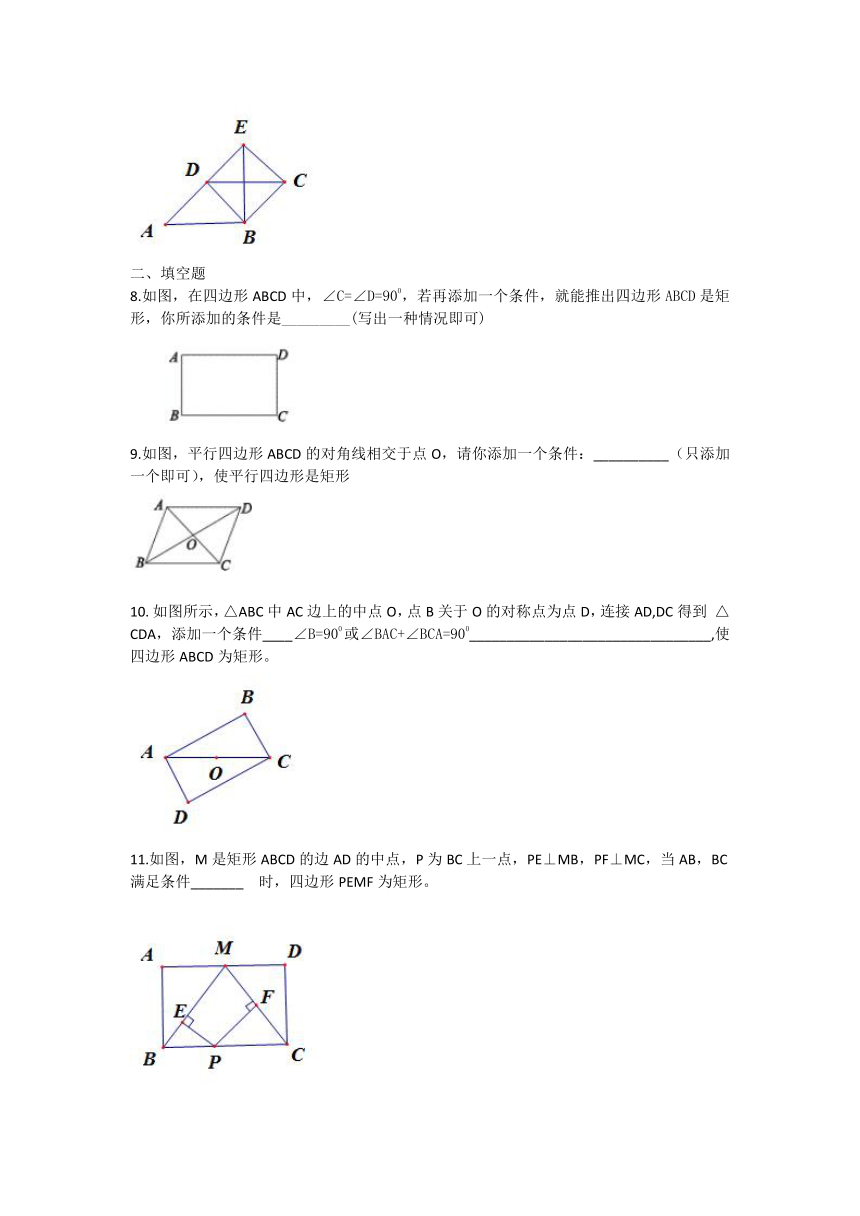
8.如图,在四边形ABCD中,∠C=∠D=900,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是_________(写出一种情况即可)
9.如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件:__________(只添加一个即可),使平行四边形是矩形
如图所示,△ABC中AC边上的中点O,点B关于O的对称点为点D,连接AD,DC得到 △CDA,添加一个条件____∠B=900或∠BAC+∠BCA=900________________________________,使四边形ABCD为矩形。
11.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MB,PF⊥MC,当AB,BC满足条件_______ 时,四边形PEMF为矩形。
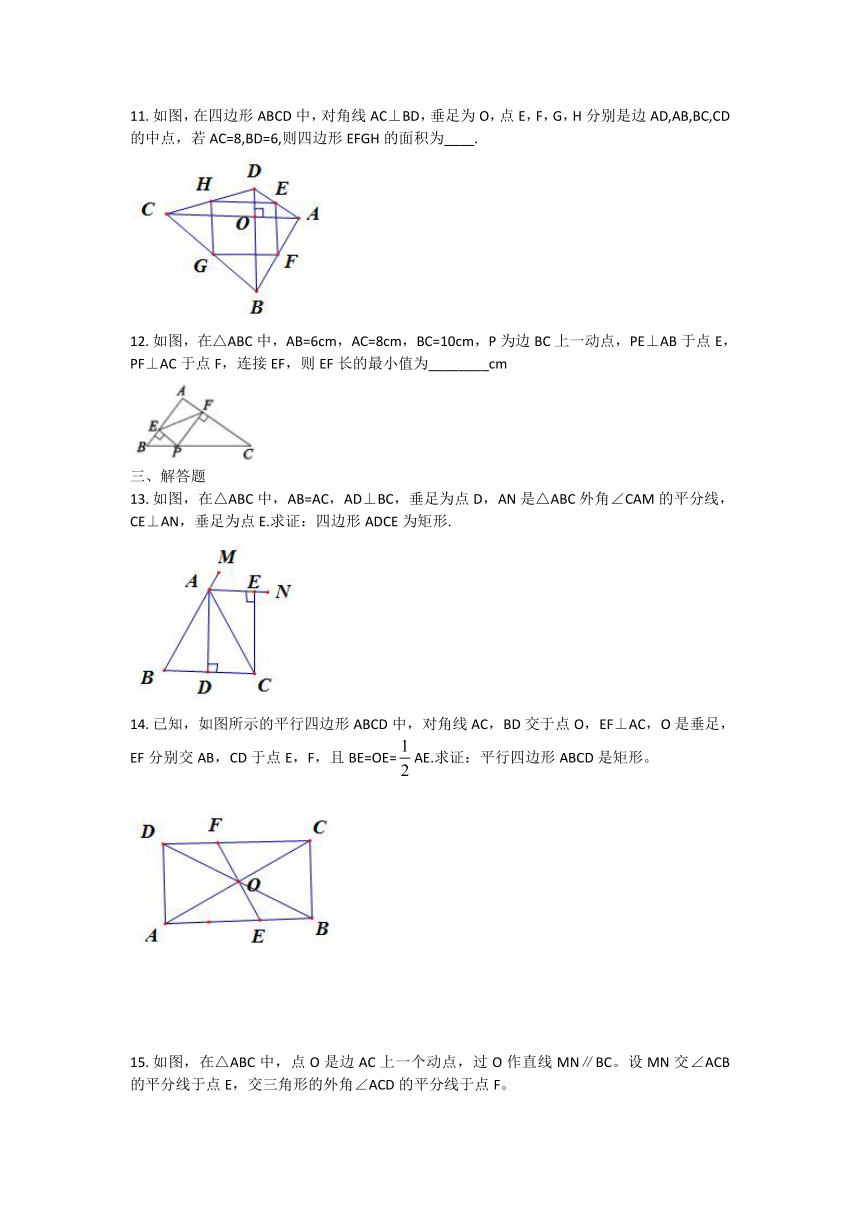
如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别是边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.
如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF长的最小值为________cm
解答题
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
已知,如图所示的平行四边形ABCD中,对角线AC,BD交于点O,EF⊥AC,O是垂足,EF分别交AB,CD于点E,F,且BE=OE=AE.求证:平行四边形ABCD是矩形。
如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC。设MN交∠ACB的平分线于点E,交三角形的外角∠ACD的平分线于点F。
求证:OE=OF;
若CE=12,CF=5,求OC的长;
当点OD在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由。
参考答案
选择题
C 2. B 3. B 4. C 5. D 6. C 7. B
填空题
∠A=900
AC=BD
BC=2AB
11. 12
12. 4.8
三、解答题
13.证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
又AN平分∠MAC
∴∠MAN=∠CAB
∴∠DAN=∠CAD+∠CAN=∠BAC+∠MAC=(∠BAC+∠MAC)=×1800=900
又AD⊥BC,CE⊥AN,
∴∠ADC=∠AEC=900.
∴四边形ACCE为矩形。
14.证明 :取AE的中点G,连接OG.
在Rt△AOE中,OG=AE=AG.
∵OE=BE=AE,
∴OE=OG=GE=AG=BE
∴△OGE为等边三角形,
∴∠EG=600,∠OAB=∠OBA=300
∴OA=OB
∴AC=BD
∴平行四边形ABCD是矩形
15.
证明:∵CF平分∠ACD,且MN∥BD,
∴∠ACF=∠FCD=∠CFO.
∴OF=OC
同理可证:OC=OE,∴OE=OF.
解:由(1)知OF=OC,OC=OE.
∴∠OCF=∠OFC, ∠OCE=∠OEC.
∴∠OCF+∠OCE=∠OFC+∠OEC.
而∠OCF+∠OCE+∠OFC+∠OEC=1800,
∴∠ECF=∠OCF+∠OCE=900,
∴OC=
解:当点O移动到AC中点时,四边形AECF为矩形,理由如下:
连接AE,AF。由(1)知OE=OF,当点O移动到AC中点时,有OA=OC,
∴四边形AECF为平行四边形,又∵∠ECF=900,∴四边形AECF为矩形。
选择题
如图,要使平行四边形ABCD成为矩形,需要添加的条件是()
∠A+∠B=1800 B. ∠B+∠C=1800 C. ∠A=∠B D. ∠B=∠D
平行四边形ABCD中,AC,BD是对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()
AB=BC B. AC=BD C. AC⊥BD D. AB⊥BD
下列关于矩形的说法中正确的是()
对角线相等的四边形是矩形
矩形的对角线相等且互相平分
对角线互相平分的四边形是矩形
矩形的对角线互相垂直且平分
检查一个门框是否为矩形,下列说法中正确的是()
测量两条对角线,是否相等
测量两条对角线,是否互相平分
测量门框的三个角,是否都是直角
测量两条对角线,是否互相垂直
如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()
AB=CD B. AD=BC C. AB=BC D. AC=BD
如图,要使平行四边形ABCD成为矩形,需添加的条件是()
AB=BD B. AC⊥BD C. ∠ABC=∠BAD D. ∠1=∠3
如图,四边形ABCD为平行四边形,延长AD至点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是()
AB=BE B. BE⊥DC C. ∠ADB=900 D.CE⊥DE
填空题
8.如图,在四边形ABCD中,∠C=∠D=900,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是_________(写出一种情况即可)
9.如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件:__________(只添加一个即可),使平行四边形是矩形
如图所示,△ABC中AC边上的中点O,点B关于O的对称点为点D,连接AD,DC得到 △CDA,添加一个条件____∠B=900或∠BAC+∠BCA=900________________________________,使四边形ABCD为矩形。
11.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MB,PF⊥MC,当AB,BC满足条件_______ 时,四边形PEMF为矩形。
如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别是边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.
如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF长的最小值为________cm
解答题
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
已知,如图所示的平行四边形ABCD中,对角线AC,BD交于点O,EF⊥AC,O是垂足,EF分别交AB,CD于点E,F,且BE=OE=AE.求证:平行四边形ABCD是矩形。
如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC。设MN交∠ACB的平分线于点E,交三角形的外角∠ACD的平分线于点F。
求证:OE=OF;
若CE=12,CF=5,求OC的长;
当点OD在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由。
参考答案
选择题
C 2. B 3. B 4. C 5. D 6. C 7. B
填空题
∠A=900
AC=BD
BC=2AB
11. 12
12. 4.8
三、解答题
13.证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
又AN平分∠MAC
∴∠MAN=∠CAB
∴∠DAN=∠CAD+∠CAN=∠BAC+∠MAC=(∠BAC+∠MAC)=×1800=900
又AD⊥BC,CE⊥AN,
∴∠ADC=∠AEC=900.
∴四边形ACCE为矩形。
14.证明 :取AE的中点G,连接OG.
在Rt△AOE中,OG=AE=AG.
∵OE=BE=AE,
∴OE=OG=GE=AG=BE
∴△OGE为等边三角形,
∴∠EG=600,∠OAB=∠OBA=300
∴OA=OB
∴AC=BD
∴平行四边形ABCD是矩形
15.
证明:∵CF平分∠ACD,且MN∥BD,
∴∠ACF=∠FCD=∠CFO.
∴OF=OC
同理可证:OC=OE,∴OE=OF.
解:由(1)知OF=OC,OC=OE.
∴∠OCF=∠OFC, ∠OCE=∠OEC.
∴∠OCF+∠OCE=∠OFC+∠OEC.
而∠OCF+∠OCE+∠OFC+∠OEC=1800,
∴∠ECF=∠OCF+∠OCE=900,
∴OC=
解:当点O移动到AC中点时,四边形AECF为矩形,理由如下:
连接AE,AF。由(1)知OE=OF,当点O移动到AC中点时,有OA=OC,
∴四边形AECF为平行四边形,又∵∠ECF=900,∴四边形AECF为矩形。
