2021年人教版数学七年级下册5.4平移课件(35张)
文档属性
| 名称 | 2021年人教版数学七年级下册5.4平移课件(35张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:25:27 | ||
图片预览









文档简介
(共35张PPT)
5.4
平移
感知生活中平移
感知生活中平移
感知生活中平移
感知生活中平移
请欣赏美丽的图案,
并思考它们有什么共同的特点?
1.这些图案有什么共同特点?
2.上面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的?
现在你能回答出刚才提出的问题了吗?
探究新知
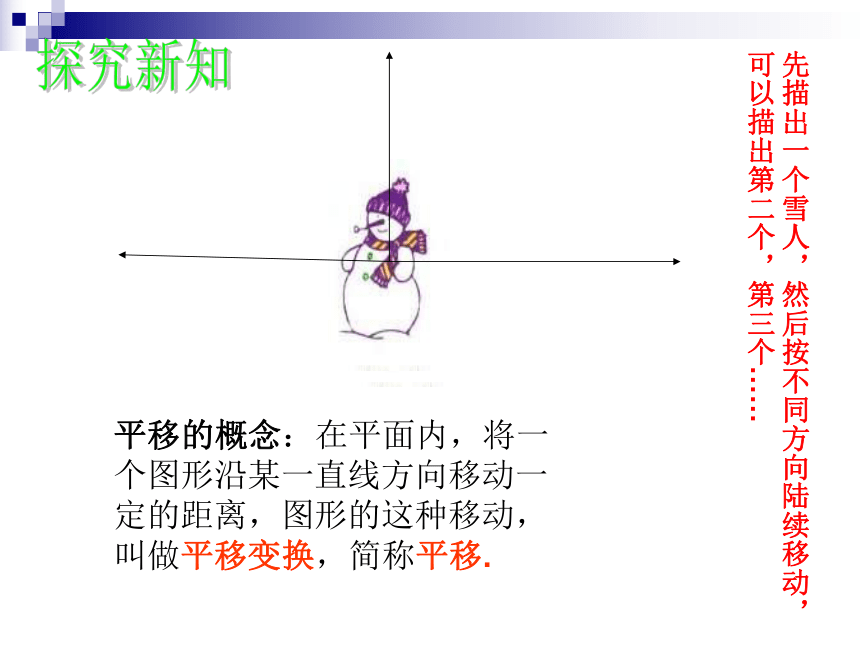
先描出一个雪人,然后按同一个方向陆续移动,可以描出第二个,第三个……
探究新知
先描出一个雪人,然后按不同方向陆续移动,可以描出第二个,第三个……
平移的概念:在平面内,将一个图形沿某一直线方向移动一定的距离,图形的这种移动,叫做平移变换,简称平移.
探究新知
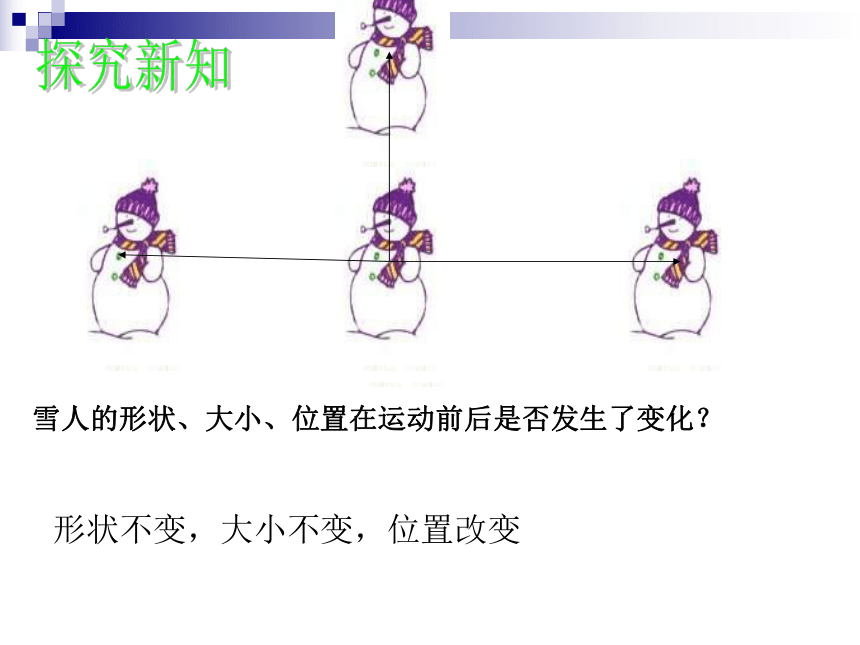
雪人的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
性质:
(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
简单说:平移后不改变图形的形状和大小.
这是平移吗?
荡秋千是平移吗?
平移
思考:图形平移的方向一定是水平方向吗?
图形平移的方向不一定是水平的或竖直的;
1.图中的变换属于平移的有哪些?
判断:
注:(1)图形平移的方向不一定是水平的。
(2)平移不改变图形的形状和大小。
(3)移动过程中图形自身方向不变,只有位置发生变化。
×
×
√
√
×
×
这些移动都是平移吗?
思考:请看图片,平移是由什么决定的?
由平移的方向和距离所决定
在所画的雪人图形中任意找三组对应点,
连接这些对应点,观察得出的线段,它们的位置、大小有什么关系?
(1)位置:AA’//BB’//CC’
(2)大小:
AA’=BB’=CC’
A
A’
A与A’是对应点!
B
B’
C
C’
探究新知
平移的第二大特点:
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等.
简单说:连接各组对应点的线段平行且相等.
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
√
巩固提高,灵活应用
(1)巩固提高
F
C
1、平移改变的是图形的(
)
A
位置
B
大小
C
形状
D
位置、大小和形状
2、经过平移,对应点所连的线段(
)
A
平行
B
相等
C
平行且相等
D
既不平行又不相等
3、经过平移,图形上每个点都沿同一个方向移动了一段距离,下面说法正确的是
(
)
A不同的点移动的距离不同
B可能相同也可能不同
C不同的点移动的距离相同
D无法确定
A
C
C
练习1:求下列2个图形的周长?
4
3
3
4
4
3
(2)灵活应用
2、北京某宾馆再重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要_____元.
5.8米
2.6米
504
3、如图,
在一块长为a米,
宽为b米的长方形地上,
有一条弯曲的柏油马路,
马路的任何地方的水平宽度都是2米.
其他部分都是草地.
求草地的面积
学习体会
通过本节课的学习,请谈谈你的收获.
(1)本节课你主要学到了什么知识?
(2)
平时要注意培养,用所学知识解决实际问题的意识。
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同。
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等。
图形的这种移动,叫做平移变换,简称平移。
空间几何体的平移:
探究
点的平移:
线的平移:
平面图形的平移:
单次平移:
多次平移:
不同方向:
同方向:
沿直线平移:
沿曲线平移:
活动与探究:
图1
是10枚硬币组成的三角形,现在只许你移动其中的3枚硬币,使图1中的三角形变成图2的倒三角形。同桌为一组,合作交流,动手移移看。
图1
图2
课后习题
1.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是___________,该点在第______象限.
2.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.
3.已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,-2)
的位置上,则点B,C的坐标分别为________,________.
(1,3)
一
(0,0)
(5,-3)
(3,-6)
课后习题
4.在平面直角坐标系中,将点A(4,1)向左平移_____单位得到点B(-1,1).
5
5.将点A(4,3)向______平移_________个单位长度后,其坐标为(4,-1).
下
4
6.正方形的四个顶点中,A(-1,2),B(3,2),C(3,-2),则第四个顶点D的坐标为_________.
(-1,-2)
课后习题
答案:A′(2,3),B′(1,0),C′(5,1).
图7-2-57
7.?如图7-2-57所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),求A′,B′,C′的坐标.
5.4
平移
感知生活中平移
感知生活中平移
感知生活中平移
感知生活中平移
请欣赏美丽的图案,
并思考它们有什么共同的特点?
1.这些图案有什么共同特点?
2.上面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的?
现在你能回答出刚才提出的问题了吗?
探究新知
先描出一个雪人,然后按同一个方向陆续移动,可以描出第二个,第三个……
探究新知
先描出一个雪人,然后按不同方向陆续移动,可以描出第二个,第三个……
平移的概念:在平面内,将一个图形沿某一直线方向移动一定的距离,图形的这种移动,叫做平移变换,简称平移.
探究新知
雪人的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
性质:
(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
简单说:平移后不改变图形的形状和大小.
这是平移吗?
荡秋千是平移吗?
平移
思考:图形平移的方向一定是水平方向吗?
图形平移的方向不一定是水平的或竖直的;
1.图中的变换属于平移的有哪些?
判断:
注:(1)图形平移的方向不一定是水平的。
(2)平移不改变图形的形状和大小。
(3)移动过程中图形自身方向不变,只有位置发生变化。
×
×
√
√
×
×
这些移动都是平移吗?
思考:请看图片,平移是由什么决定的?
由平移的方向和距离所决定
在所画的雪人图形中任意找三组对应点,
连接这些对应点,观察得出的线段,它们的位置、大小有什么关系?
(1)位置:AA’//BB’//CC’
(2)大小:
AA’=BB’=CC’
A
A’
A与A’是对应点!
B
B’
C
C’
探究新知
平移的第二大特点:
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等.
简单说:连接各组对应点的线段平行且相等.
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
√
巩固提高,灵活应用
(1)巩固提高
F
C
1、平移改变的是图形的(
)
A
位置
B
大小
C
形状
D
位置、大小和形状
2、经过平移,对应点所连的线段(
)
A
平行
B
相等
C
平行且相等
D
既不平行又不相等
3、经过平移,图形上每个点都沿同一个方向移动了一段距离,下面说法正确的是
(
)
A不同的点移动的距离不同
B可能相同也可能不同
C不同的点移动的距离相同
D无法确定
A
C
C
练习1:求下列2个图形的周长?
4
3
3
4
4
3
(2)灵活应用
2、北京某宾馆再重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要_____元.
5.8米
2.6米
504
3、如图,
在一块长为a米,
宽为b米的长方形地上,
有一条弯曲的柏油马路,
马路的任何地方的水平宽度都是2米.
其他部分都是草地.
求草地的面积
学习体会
通过本节课的学习,请谈谈你的收获.
(1)本节课你主要学到了什么知识?
(2)
平时要注意培养,用所学知识解决实际问题的意识。
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同。
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等。
图形的这种移动,叫做平移变换,简称平移。
空间几何体的平移:
探究
点的平移:
线的平移:
平面图形的平移:
单次平移:
多次平移:
不同方向:
同方向:
沿直线平移:
沿曲线平移:
活动与探究:
图1
是10枚硬币组成的三角形,现在只许你移动其中的3枚硬币,使图1中的三角形变成图2的倒三角形。同桌为一组,合作交流,动手移移看。
图1
图2
课后习题
1.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是___________,该点在第______象限.
2.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.
3.已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,-2)
的位置上,则点B,C的坐标分别为________,________.
(1,3)
一
(0,0)
(5,-3)
(3,-6)
课后习题
4.在平面直角坐标系中,将点A(4,1)向左平移_____单位得到点B(-1,1).
5
5.将点A(4,3)向______平移_________个单位长度后,其坐标为(4,-1).
下
4
6.正方形的四个顶点中,A(-1,2),B(3,2),C(3,-2),则第四个顶点D的坐标为_________.
(-1,-2)
课后习题
答案:A′(2,3),B′(1,0),C′(5,1).
图7-2-57
7.?如图7-2-57所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),求A′,B′,C′的坐标.
