第六章 圆周运动 培优训练word版含答案
文档属性
| 名称 | 第六章 圆周运动 培优训练word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 740.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览



文档简介
第六章 圆周运动
一、选择题
1.2019年1月1日,美国宇航局(NASA)“新视野号”探测器再创历史,成功飞掠柯伊伯带小天体“天涯海角”,图为探测器拍摄到该小天体的“哑铃”状照片示意图,该小天体绕固定轴匀速自转,其上有到转轴距离不等的两点A、B(LA>LB),关于这两点运动的描述,下列说法正确的是( )
A.两点线速度相同
B.A点的线速度恒定
C.两点角速度相同
D.相同时间内A、B两点通过的弧长相等
2.如图所示,O、O′为两个皮带轮,O轮的半径为r,O′轮的半径为R,且R>r,M点为O轮边缘上的一点,N点为O′轮上的任意一点,当皮带轮转动时,(设转动过程中不打滑)则( )
A.M点的向心加速度一定大于N点的向心加速度
B.M点的向心加速度一定等于N点的向心加速度
C.M点的向心加速度可能小于N点的向心加速度
D.M点的向心加速度可能等于N点的向心加速度
3.一中学生沿400米圆形跑道,跑了全长的四分之三,用时一分钟.中学生运动的角速度大小为( )
A.5 rad/s B. rad/s
C. rad/s D. rad/s
4.如图所示,在圆规匀速转动画圆的过程中( )
A.笔尖的角速度不变
B.笔尖的线速度不变
C.笔尖的加速度不变
D.笔尖在相等的时间内转过的位移不变
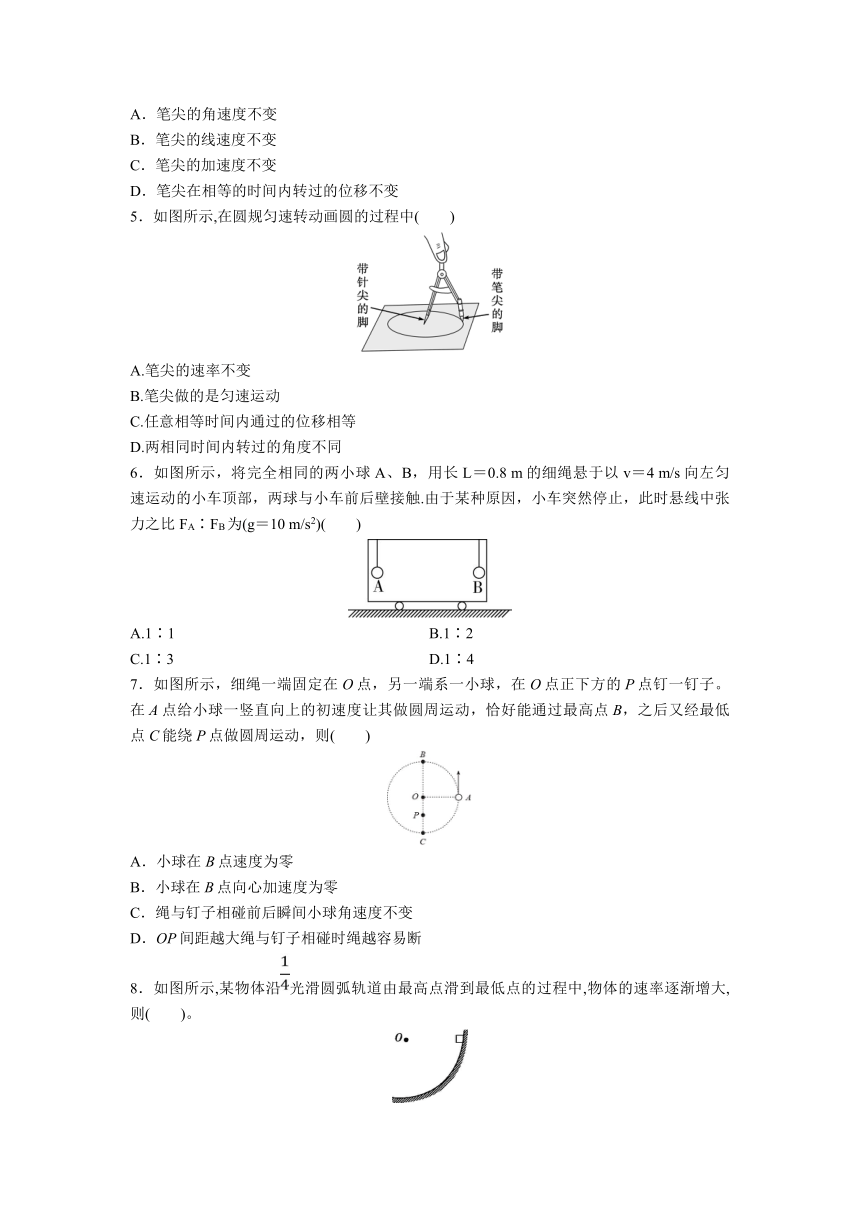
5.如图所示,在圆规匀速转动画圆的过程中( )
A.笔尖的速率不变
B.笔尖做的是匀速运动
C.任意相等时间内通过的位移相等
D.两相同时间内转过的角度不同
6.如图所示,将完全相同的两小球A、B,用长L=0.8 m的细绳悬于以v=4 m/s向左匀速运动的小车顶部,两球与小车前后壁接触.由于某种原因,小车突然停止,此时悬线中张力之比FA∶FB为(g=10 m/s2)( )
A.1∶1 B.1∶2
C.1∶3 D.1∶4
7.如图所示,细绳一端固定在O点,另一端系一小球,在O点正下方的P点钉一钉子。在A点给小球一竖直向上的初速度让其做圆周运动,恰好能通过最高点B,之后又经最低点C能绕P点做圆周运动,则( )
A.小球在B点速度为零
B.小球在B点向心加速度为零
C.绳与钉子相碰前后瞬间小球角速度不变
D.OP间距越大绳与钉子相碰时绳越容易断
8.如图所示,某物体沿光滑圆弧轨道由最高点滑到最低点的过程中,物体的速率逐渐增大,则( )。
A.物体受到的合力为零
B.物体受到的合力大小不变,方向始终指向圆心O
C.物体受到的合力就是向心力
D.物体的合力方向始终与其运动方向不垂直(最低点除外)
二、多选题
9.(多选)2013年6月11日至26日,“神舟十号”飞船圆满完成了太空之行,期间还成功进行了人类历史上第二次太空授课,女航天员王亚平做了大量失重状态下的精美物理实验。如图所示为处于完全失重状态下的陀螺,下列说法正确的是( )
A.陀螺仍受重力的作用
B.陀螺受力平衡
C.陀螺所受重力等于所需的向心力
D.陀螺不受重力的作用
10.(多选)如图所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔的水平桌面上,小球在某一水平面内做匀速圆周运动(圆锥摆).现使小球改到一个更高一些的水平面上做匀速圆周运动(图上未画出),两次金属块Q都保持在桌面上静止.则后一种情况与原来相比较,下面的判断中正确的是( )
A.Q受到桌面的支持力变大
B.Q受到桌面的静摩擦力变大
C.小球P运动的角速度变大
D.小球P运动的周期变大
11.(多选)洗衣机的脱水筒采用带动衣物旋转的方式脱水,下列说法正确的是 ( )
A.脱水过程中,衣物是紧贴筒壁的
B.加快脱水筒转动角速度,脱水效果会更好
C.靠近中心的衣物脱水效果不如四周的衣物脱水效果好
D.水会从筒中甩出是因为水滴受到的向心力很大
12.(多选)如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细绳相连的质量均为m的两个物体A和B,它们分居圆心两侧,与圆心距离分别为RA=r,RB=2r,两物体与盘间的动摩擦因数μ相同,当圆盘转速缓慢加快到两物体刚好要发生滑动时,最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )。
A.此时绳子的张力为3μmg
B.此时A所受摩擦力方向沿半径指向圆内
C.此时圆盘的角速度为
D.此时烧断绳子,A仍相对盘静止,B将做离心运动
三、解答题
13.用如图所示的装置来探究小球做圆周运动所需向心力的大小F与质量m、角速度ω和半径r之间的关系。两个变速塔轮通过皮带连接,转动手柄使长槽和短槽分别随变速塔轮匀速转动,槽内的钢球就做匀速圆周运动。横臂的挡板对钢球的压力提供向心力,钢球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上的红白相间的等分格显示出两个钢球所受向心力的比值。如图是探究过程中某次实验时装置的状态。
(1)在研究向心力的大小F与质量m关系时,要保持 相同。?
A.ω和r B.ω和m
C.m和r D. m和F
(2)图中所示,两个钢球质量和半径相等,则是在研究向心力的大小F与 的关系。?
A.质量m B.半径r C.角速度ω
(3)若图中标尺上红白相间的等分格显示出两个钢球所受向心力的比值为1∶9,与皮带连接的两个变速塔轮的半径之比为 。?
A.1∶3 B.3∶1 C.1∶9 D.9∶1
14.如图甲所示,同学们分小组探究影响向心力大小的因素。同学们用细绳系一纸杯(杯中有30 mL的水)在空中甩动,使杯在水平面内做圆周运动,来感受向心力。
甲 乙
(1)下列说法中正确的是________。
A.保持质量、绳长不变,增大转速,绳对手的拉力将不变
B.保持质量、绳长不变,增大转速,绳对手的拉力将增大
C.保持质量、角速度不变,增大绳长,绳对手的拉力将不变
D.保持质量、角速度不变,增大绳长,绳对手的拉力将增大
(2)如图乙所示,绳离杯心40 cm处打一结点A,80 cm处打一结点B,学习小组中一位同学手表计时,另一位同学操作,其余同学记录实验数据。
操作一:手握绳结A,使杯在水平方向每秒运动一周,体会向心力的大小。
操作二:手握绳结B,使杯在水平方向每秒运动一周,体会向心力的大小。
操作三:手握绳结A,使杯在水平方向每秒运动二周,体会向心力的大小。
操作四:手握绳结A,再向杯中添加30 mL的水,使杯在水平方向每秒运动一周,体会向心力的大小。
则:①操作二与一相比较:质量、角速度相同,向心力的大小与转动半径大小有关;
操作三与一相比较:质量、半径相同,向心力的大小与角速度的大小有关;
操作四与一相比较:________________相同, 向心力大小与________有关;
②物理学中此种实验方法叫________法。
四、计算题
15.如图所示,游乐场翻滚过山车上的乘客常常会在高速旋转或高空倒悬时吓得魂飞魄散,但这种车的设计有足够的安全系数,过山车在做圆周运动时可以使乘客稳坐在座椅上,还有安全棒紧紧压在乘客胸前,在过山车未到达终点以前,谁也无法将它们打开。设想如下数据,轨道最高处离地面32 m,最低处几乎贴地,圆环直径为15 m,过山车经过最低点时的速度约为25 m/s,经过圆环最高点时的速度约为18 m/s。试利用牛顿第二定律和圆周运动的知识,探究这样的情况下能否保证乘客的安全(取g=10 m/s2)?
16.有一列质量为100 t的火车,以72 km/h的速率匀速通过一个内外轨一样高的弯道,轨道半径为400 m。
(1)请计算铁轨受到的侧压力。
(2)若要使火车以此速率通过弯道,且使铁轨所受侧压力为零,我们可以适当倾斜路基,请计算火车对铁轨的压力大小。(取g=10 m/s2)
17.在我国南方山区有一种简易水轮机,如图所示,从悬崖上流出的水可看作连续做平抛运动的物体,水流轨迹与下边放置的轮子边沿相切,水冲击轮子边缘上安装的挡水板,可使轮子连续转动,输出动力。当该系统工作稳定时,可近似认为水的末速度与轮子边缘的线速度相同。设水的流出点比轮轴高h=5.6 m,轮子半径R=1 m。调整轮轴O的位置,使水流与轮边缘切点相对应的半径与水平线成37°。取g=10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)求水流的初速度v0的大小。
(2)若不计挡水板的大小,则轮子转动的角速度为多少?
参考答案
一、选择题
1.C
【解析】
A、B两点同轴转动,故A、B的角速度相等,LA>LB,根据v=rω得,两点线速度不相同,选项A错误,C正确;A点的线速度方向时刻改变,选项B错误;A、B两点的线速度不一致,所以相同时间内A、B两点通过的弧长不相等,选项D错误。
2.A
【解析】
在O′轮的边缘上取一点Q,则Q点和N点在同一个轮子上,其角速度相等,即ωQ=ωN,又rQ>rN,由向心加速度公式an=ω2r可知aQ>aN;由于皮带转动时不打滑,Q点和M点都在由皮带传动的两个轮子边缘上,这两点的线速度大小相等,即vQ=vM,又rQ>rM,由向心加速度公式an=可知,aQaN,A正确.
3.C
解析: C
根据题意可知匀速圆周运动的弧长为s=300 m,是全长的四分之三,可知转过的圆心角为θ=×2π rad=π rad,时间为t=60 s,由角速度的定义式ω==π rad/s,故A、B、D错误,C正确.
4.A
【解析】
做匀速圆周运动的物体角速度是不变的,故A正确;线速度是矢量,在匀速转动圆规画图的过程中,线速度大小不变,方向时刻改变,所以笔尖的线速度是变化的,故B错误;笔尖的加速度大小不变,方向时刻改变,所以笔尖的加速度是变化的,故C错误;笔尖在相同时间内转过的路程相等,但转过的位移不一定相等,故D错误.
5.A
【解析】
由线速度定义知,匀速圆周运动的速度大小不变,也就是速率不变,但速度的方向时刻改变,故A正确,B错误;做匀速圆周运动的物体在任意相等时间内通过的弧长相等,但位移还要考虑方向,C错误;相同时间内转过角度相同,D错误。
6.C
【解析】
小车突然停止,B球将做圆周运动,所以FB=m+mg=30m;A球做水平方向减速运动,FA=mg=10m,故此时悬线中张力之比为FA∶FB=1∶3,故C项正确.
7.D
【解析】
小球恰能经过最高点B,则,可得vB=,A错误;小球在B点向心加速度,B错误;绳与钉子相碰前后瞬间小球线速度不变,半径减小,则角速度变大,C错误;根据,可得,OP间距越大,则R越小,T越大,则绳与钉子相碰时绳越容易断,D正确。
8.D
【解析】
物体做圆周运动,一定有外力提供向心力,合力一定不为零,A项错误;物体做圆周运动,一定有指向圆心的外力提供向心力,物体的速率增大,一定有沿圆弧切线方向的分力,根据平行四边形定则可知,物体的合力方向始终与其运动方向不垂直,最低点除外,B、C两项错误,D项正确。
二、多选题
9.AC
【解析】
做匀速圆周运动的空间站中的物体,所受重力全部提供其做圆周运动的向心力,处于完全失重状态,并非不受重力作用,A、C正确,B、D错误。
10.BC
【解析】
金属块Q保持在桌面上静止,对于金属块和小球整体研究,整体在竖直方向没有加速度,根据平衡条件得知,Q受到桌面的支持力等于两个物体的总重力,保持不变,故A错误.设细线与竖直方向的夹角为θ,细线的拉力大小为T,细线的长度为L.P球做匀速圆周运动时,由重力和细线的拉力的合力提供向心力,如图,则有T=,mgtan θ=mω2Lsin θ,得角速度ω==,周期T=,使小球改到一个更高一些的水平面上做匀速圆周运动时,θ增大,cos θ减小、h减小,则得到细线拉力T增大,角速度增大,周期T减小.对Q,由平衡条件得知,f=Tsin θ=mgtan θ,知Q受到桌面的静摩擦力变大,静摩擦力方向在改变,故B、C正确,D错误.
11.ABC
【解析】
脱水过程中,衣物做离心运动而甩向筒壁,故A正确;F=ma=mω2R,ω增大会使向心力F增大,而转筒有洞,不能提供足够大的向心力,水滴就会被甩出去,增大向心力,会使更多水滴被甩出去,脱水效果会更好,故B正确;中心的衣服,R比较小,角速度ω一样,所以向心力小,脱水效果差,故C正确;水滴依附的附着力是一定的,当水滴因做圆周运动所需的向心力大于该附着力时,水滴被甩掉,故D错误.
12.AC
【解析】
两物块A和B随着圆盘转动时,合外力提供向心力,B的半径比A的半径大,所以B所需向心力大,绳子拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,B的最大静摩擦力方向指向圆心,A的最大静摩擦力方向指向圆外,根据牛顿第二定律得T-μmg=mω2r,T+μmg=mω2·2r,解得T=3μmg,ω=,故A、C两项正确,B项错误。烧断绳子瞬间A物体所需的向心力为2μmg,A的最大静摩擦力不足以提供向心力,则A做离心运动,D项错误。
三、解答题
13.(1)A (2)C (3)B
14.(1)BD (2)①角速度、半径 质量 ②控制变量
四、计算题
15.首先分析一下当过山车运动到圆环底部和圆环顶部时过山车中人的受力情况:重力mg,FN下和FN上,FN下和FN上分别为过山车在圆环底部和顶部时圆环对人的支持力(为简化问题,可不考虑摩擦及空气阻力)。我们知道,过山车沿圆环运动,人也在做圆周运动,这时人做圆周运动所需的向心力由mg和FN提供。要保证安全,则需FN>0,即人牢牢地与座椅在一起,用v下表示人在圆环底部的速度,v上表示人在圆环顶部的速度,R表示圆环的半径,则
在底部:FN下-mg=m, ①
在顶部:FN上+mg=m, ②
由①式可知,FN下=mg+m,即在圆环底部时,过山车对人的支持力比人的重力增大了m,这时人对座椅的压力自然也比重力大m,就好像人的重力增加了m,使人紧压在座椅上不能动弹,故人在圆环最低点是安全的。
恰好能通过顶部的速度v0=≈8.7 m/s,
而过山车通过顶点时的速度约为18 m/s,比8.7 m/s大得多,此时人与座椅间也有较大的压力,所以过山车和人一定能安全地通过圆环最高点。
16.(1)轨道对火车的侧压力提供火车做圆周运动的向心力,有FN=m=1×105 N
由牛顿第三定律知外轨受到的侧压力FN'=1×105 N,指向轨道半径方向。
(2)设铁轨平面与地面的夹角为α,则
mgtan α=m,tan α==0.1
火车对铁轨的压力大小F==1.01×106 N。
17.(1)流出的水做平抛运动,设在空中运动的时间为t,在竖直方向有h-Rsin θ=gt2
代入数据解得t=1 s
由合速度与分速度的关系有tan θ=
解得v0=7.5 m/s。
(2)设水与轮接触时的速度大小为v,则有v==12.5 m/s
设轮子转动的角速度为ω,由于水的末速度与轮子边缘的线速度相同,则有ω==12.5 rad/s。
一、选择题
1.2019年1月1日,美国宇航局(NASA)“新视野号”探测器再创历史,成功飞掠柯伊伯带小天体“天涯海角”,图为探测器拍摄到该小天体的“哑铃”状照片示意图,该小天体绕固定轴匀速自转,其上有到转轴距离不等的两点A、B(LA>LB),关于这两点运动的描述,下列说法正确的是( )
A.两点线速度相同
B.A点的线速度恒定
C.两点角速度相同
D.相同时间内A、B两点通过的弧长相等
2.如图所示,O、O′为两个皮带轮,O轮的半径为r,O′轮的半径为R,且R>r,M点为O轮边缘上的一点,N点为O′轮上的任意一点,当皮带轮转动时,(设转动过程中不打滑)则( )
A.M点的向心加速度一定大于N点的向心加速度
B.M点的向心加速度一定等于N点的向心加速度
C.M点的向心加速度可能小于N点的向心加速度
D.M点的向心加速度可能等于N点的向心加速度
3.一中学生沿400米圆形跑道,跑了全长的四分之三,用时一分钟.中学生运动的角速度大小为( )
A.5 rad/s B. rad/s
C. rad/s D. rad/s
4.如图所示,在圆规匀速转动画圆的过程中( )
A.笔尖的角速度不变
B.笔尖的线速度不变
C.笔尖的加速度不变
D.笔尖在相等的时间内转过的位移不变
5.如图所示,在圆规匀速转动画圆的过程中( )
A.笔尖的速率不变
B.笔尖做的是匀速运动
C.任意相等时间内通过的位移相等
D.两相同时间内转过的角度不同
6.如图所示,将完全相同的两小球A、B,用长L=0.8 m的细绳悬于以v=4 m/s向左匀速运动的小车顶部,两球与小车前后壁接触.由于某种原因,小车突然停止,此时悬线中张力之比FA∶FB为(g=10 m/s2)( )
A.1∶1 B.1∶2
C.1∶3 D.1∶4
7.如图所示,细绳一端固定在O点,另一端系一小球,在O点正下方的P点钉一钉子。在A点给小球一竖直向上的初速度让其做圆周运动,恰好能通过最高点B,之后又经最低点C能绕P点做圆周运动,则( )
A.小球在B点速度为零
B.小球在B点向心加速度为零
C.绳与钉子相碰前后瞬间小球角速度不变
D.OP间距越大绳与钉子相碰时绳越容易断
8.如图所示,某物体沿光滑圆弧轨道由最高点滑到最低点的过程中,物体的速率逐渐增大,则( )。
A.物体受到的合力为零
B.物体受到的合力大小不变,方向始终指向圆心O
C.物体受到的合力就是向心力
D.物体的合力方向始终与其运动方向不垂直(最低点除外)
二、多选题
9.(多选)2013年6月11日至26日,“神舟十号”飞船圆满完成了太空之行,期间还成功进行了人类历史上第二次太空授课,女航天员王亚平做了大量失重状态下的精美物理实验。如图所示为处于完全失重状态下的陀螺,下列说法正确的是( )
A.陀螺仍受重力的作用
B.陀螺受力平衡
C.陀螺所受重力等于所需的向心力
D.陀螺不受重力的作用
10.(多选)如图所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔的水平桌面上,小球在某一水平面内做匀速圆周运动(圆锥摆).现使小球改到一个更高一些的水平面上做匀速圆周运动(图上未画出),两次金属块Q都保持在桌面上静止.则后一种情况与原来相比较,下面的判断中正确的是( )
A.Q受到桌面的支持力变大
B.Q受到桌面的静摩擦力变大
C.小球P运动的角速度变大
D.小球P运动的周期变大
11.(多选)洗衣机的脱水筒采用带动衣物旋转的方式脱水,下列说法正确的是 ( )
A.脱水过程中,衣物是紧贴筒壁的
B.加快脱水筒转动角速度,脱水效果会更好
C.靠近中心的衣物脱水效果不如四周的衣物脱水效果好
D.水会从筒中甩出是因为水滴受到的向心力很大
12.(多选)如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细绳相连的质量均为m的两个物体A和B,它们分居圆心两侧,与圆心距离分别为RA=r,RB=2r,两物体与盘间的动摩擦因数μ相同,当圆盘转速缓慢加快到两物体刚好要发生滑动时,最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )。
A.此时绳子的张力为3μmg
B.此时A所受摩擦力方向沿半径指向圆内
C.此时圆盘的角速度为
D.此时烧断绳子,A仍相对盘静止,B将做离心运动
三、解答题
13.用如图所示的装置来探究小球做圆周运动所需向心力的大小F与质量m、角速度ω和半径r之间的关系。两个变速塔轮通过皮带连接,转动手柄使长槽和短槽分别随变速塔轮匀速转动,槽内的钢球就做匀速圆周运动。横臂的挡板对钢球的压力提供向心力,钢球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上的红白相间的等分格显示出两个钢球所受向心力的比值。如图是探究过程中某次实验时装置的状态。
(1)在研究向心力的大小F与质量m关系时,要保持 相同。?
A.ω和r B.ω和m
C.m和r D. m和F
(2)图中所示,两个钢球质量和半径相等,则是在研究向心力的大小F与 的关系。?
A.质量m B.半径r C.角速度ω
(3)若图中标尺上红白相间的等分格显示出两个钢球所受向心力的比值为1∶9,与皮带连接的两个变速塔轮的半径之比为 。?
A.1∶3 B.3∶1 C.1∶9 D.9∶1
14.如图甲所示,同学们分小组探究影响向心力大小的因素。同学们用细绳系一纸杯(杯中有30 mL的水)在空中甩动,使杯在水平面内做圆周运动,来感受向心力。
甲 乙
(1)下列说法中正确的是________。
A.保持质量、绳长不变,增大转速,绳对手的拉力将不变
B.保持质量、绳长不变,增大转速,绳对手的拉力将增大
C.保持质量、角速度不变,增大绳长,绳对手的拉力将不变
D.保持质量、角速度不变,增大绳长,绳对手的拉力将增大
(2)如图乙所示,绳离杯心40 cm处打一结点A,80 cm处打一结点B,学习小组中一位同学手表计时,另一位同学操作,其余同学记录实验数据。
操作一:手握绳结A,使杯在水平方向每秒运动一周,体会向心力的大小。
操作二:手握绳结B,使杯在水平方向每秒运动一周,体会向心力的大小。
操作三:手握绳结A,使杯在水平方向每秒运动二周,体会向心力的大小。
操作四:手握绳结A,再向杯中添加30 mL的水,使杯在水平方向每秒运动一周,体会向心力的大小。
则:①操作二与一相比较:质量、角速度相同,向心力的大小与转动半径大小有关;
操作三与一相比较:质量、半径相同,向心力的大小与角速度的大小有关;
操作四与一相比较:________________相同, 向心力大小与________有关;
②物理学中此种实验方法叫________法。
四、计算题
15.如图所示,游乐场翻滚过山车上的乘客常常会在高速旋转或高空倒悬时吓得魂飞魄散,但这种车的设计有足够的安全系数,过山车在做圆周运动时可以使乘客稳坐在座椅上,还有安全棒紧紧压在乘客胸前,在过山车未到达终点以前,谁也无法将它们打开。设想如下数据,轨道最高处离地面32 m,最低处几乎贴地,圆环直径为15 m,过山车经过最低点时的速度约为25 m/s,经过圆环最高点时的速度约为18 m/s。试利用牛顿第二定律和圆周运动的知识,探究这样的情况下能否保证乘客的安全(取g=10 m/s2)?
16.有一列质量为100 t的火车,以72 km/h的速率匀速通过一个内外轨一样高的弯道,轨道半径为400 m。
(1)请计算铁轨受到的侧压力。
(2)若要使火车以此速率通过弯道,且使铁轨所受侧压力为零,我们可以适当倾斜路基,请计算火车对铁轨的压力大小。(取g=10 m/s2)
17.在我国南方山区有一种简易水轮机,如图所示,从悬崖上流出的水可看作连续做平抛运动的物体,水流轨迹与下边放置的轮子边沿相切,水冲击轮子边缘上安装的挡水板,可使轮子连续转动,输出动力。当该系统工作稳定时,可近似认为水的末速度与轮子边缘的线速度相同。设水的流出点比轮轴高h=5.6 m,轮子半径R=1 m。调整轮轴O的位置,使水流与轮边缘切点相对应的半径与水平线成37°。取g=10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)求水流的初速度v0的大小。
(2)若不计挡水板的大小,则轮子转动的角速度为多少?
参考答案
一、选择题
1.C
【解析】
A、B两点同轴转动,故A、B的角速度相等,LA>LB,根据v=rω得,两点线速度不相同,选项A错误,C正确;A点的线速度方向时刻改变,选项B错误;A、B两点的线速度不一致,所以相同时间内A、B两点通过的弧长不相等,选项D错误。
2.A
【解析】
在O′轮的边缘上取一点Q,则Q点和N点在同一个轮子上,其角速度相等,即ωQ=ωN,又rQ>rN,由向心加速度公式an=ω2r可知aQ>aN;由于皮带转动时不打滑,Q点和M点都在由皮带传动的两个轮子边缘上,这两点的线速度大小相等,即vQ=vM,又rQ>rM,由向心加速度公式an=可知,aQ
3.C
解析: C
根据题意可知匀速圆周运动的弧长为s=300 m,是全长的四分之三,可知转过的圆心角为θ=×2π rad=π rad,时间为t=60 s,由角速度的定义式ω==π rad/s,故A、B、D错误,C正确.
4.A
【解析】
做匀速圆周运动的物体角速度是不变的,故A正确;线速度是矢量,在匀速转动圆规画图的过程中,线速度大小不变,方向时刻改变,所以笔尖的线速度是变化的,故B错误;笔尖的加速度大小不变,方向时刻改变,所以笔尖的加速度是变化的,故C错误;笔尖在相同时间内转过的路程相等,但转过的位移不一定相等,故D错误.
5.A
【解析】
由线速度定义知,匀速圆周运动的速度大小不变,也就是速率不变,但速度的方向时刻改变,故A正确,B错误;做匀速圆周运动的物体在任意相等时间内通过的弧长相等,但位移还要考虑方向,C错误;相同时间内转过角度相同,D错误。
6.C
【解析】
小车突然停止,B球将做圆周运动,所以FB=m+mg=30m;A球做水平方向减速运动,FA=mg=10m,故此时悬线中张力之比为FA∶FB=1∶3,故C项正确.
7.D
【解析】
小球恰能经过最高点B,则,可得vB=,A错误;小球在B点向心加速度,B错误;绳与钉子相碰前后瞬间小球线速度不变,半径减小,则角速度变大,C错误;根据,可得,OP间距越大,则R越小,T越大,则绳与钉子相碰时绳越容易断,D正确。
8.D
【解析】
物体做圆周运动,一定有外力提供向心力,合力一定不为零,A项错误;物体做圆周运动,一定有指向圆心的外力提供向心力,物体的速率增大,一定有沿圆弧切线方向的分力,根据平行四边形定则可知,物体的合力方向始终与其运动方向不垂直,最低点除外,B、C两项错误,D项正确。
二、多选题
9.AC
【解析】
做匀速圆周运动的空间站中的物体,所受重力全部提供其做圆周运动的向心力,处于完全失重状态,并非不受重力作用,A、C正确,B、D错误。
10.BC
【解析】
金属块Q保持在桌面上静止,对于金属块和小球整体研究,整体在竖直方向没有加速度,根据平衡条件得知,Q受到桌面的支持力等于两个物体的总重力,保持不变,故A错误.设细线与竖直方向的夹角为θ,细线的拉力大小为T,细线的长度为L.P球做匀速圆周运动时,由重力和细线的拉力的合力提供向心力,如图,则有T=,mgtan θ=mω2Lsin θ,得角速度ω==,周期T=,使小球改到一个更高一些的水平面上做匀速圆周运动时,θ增大,cos θ减小、h减小,则得到细线拉力T增大,角速度增大,周期T减小.对Q,由平衡条件得知,f=Tsin θ=mgtan θ,知Q受到桌面的静摩擦力变大,静摩擦力方向在改变,故B、C正确,D错误.
11.ABC
【解析】
脱水过程中,衣物做离心运动而甩向筒壁,故A正确;F=ma=mω2R,ω增大会使向心力F增大,而转筒有洞,不能提供足够大的向心力,水滴就会被甩出去,增大向心力,会使更多水滴被甩出去,脱水效果会更好,故B正确;中心的衣服,R比较小,角速度ω一样,所以向心力小,脱水效果差,故C正确;水滴依附的附着力是一定的,当水滴因做圆周运动所需的向心力大于该附着力时,水滴被甩掉,故D错误.
12.AC
【解析】
两物块A和B随着圆盘转动时,合外力提供向心力,B的半径比A的半径大,所以B所需向心力大,绳子拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,B的最大静摩擦力方向指向圆心,A的最大静摩擦力方向指向圆外,根据牛顿第二定律得T-μmg=mω2r,T+μmg=mω2·2r,解得T=3μmg,ω=,故A、C两项正确,B项错误。烧断绳子瞬间A物体所需的向心力为2μmg,A的最大静摩擦力不足以提供向心力,则A做离心运动,D项错误。
三、解答题
13.(1)A (2)C (3)B
14.(1)BD (2)①角速度、半径 质量 ②控制变量
四、计算题
15.首先分析一下当过山车运动到圆环底部和圆环顶部时过山车中人的受力情况:重力mg,FN下和FN上,FN下和FN上分别为过山车在圆环底部和顶部时圆环对人的支持力(为简化问题,可不考虑摩擦及空气阻力)。我们知道,过山车沿圆环运动,人也在做圆周运动,这时人做圆周运动所需的向心力由mg和FN提供。要保证安全,则需FN>0,即人牢牢地与座椅在一起,用v下表示人在圆环底部的速度,v上表示人在圆环顶部的速度,R表示圆环的半径,则
在底部:FN下-mg=m, ①
在顶部:FN上+mg=m, ②
由①式可知,FN下=mg+m,即在圆环底部时,过山车对人的支持力比人的重力增大了m,这时人对座椅的压力自然也比重力大m,就好像人的重力增加了m,使人紧压在座椅上不能动弹,故人在圆环最低点是安全的。
恰好能通过顶部的速度v0=≈8.7 m/s,
而过山车通过顶点时的速度约为18 m/s,比8.7 m/s大得多,此时人与座椅间也有较大的压力,所以过山车和人一定能安全地通过圆环最高点。
16.(1)轨道对火车的侧压力提供火车做圆周运动的向心力,有FN=m=1×105 N
由牛顿第三定律知外轨受到的侧压力FN'=1×105 N,指向轨道半径方向。
(2)设铁轨平面与地面的夹角为α,则
mgtan α=m,tan α==0.1
火车对铁轨的压力大小F==1.01×106 N。
17.(1)流出的水做平抛运动,设在空中运动的时间为t,在竖直方向有h-Rsin θ=gt2
代入数据解得t=1 s
由合速度与分速度的关系有tan θ=
解得v0=7.5 m/s。
(2)设水与轮接触时的速度大小为v,则有v==12.5 m/s
设轮子转动的角速度为ω,由于水的末速度与轮子边缘的线速度相同,则有ω==12.5 rad/s。
