2020-2021学年高一数学人教A版必修4第二章2.1 平面向量的实际背景及基本概念2课时课件(共40张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第二章2.1 平面向量的实际背景及基本概念2课时课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 21:33:50 | ||
图片预览










文档简介
第二章
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
2.1
平面向量的实际背景
及基本概念
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
2.1.1
2.1.2
向量的物理背景与概念
向量的几何表示
返回目录
学习要点
1. 什么是有向线段? 有向线段包含哪三个要素? 有向线段的记法和图形表示是怎样的?
2. 什么是向量? 它由几个要素构成?
3. 向量的几何表示与字母表示分别是怎样的?
4. 什么是零向量? 什么是单位向量? 零向量是怎样表示的?
5. 什么是向量的模? 它是怎样表示法?
2.1.1 向量的物理背景与概念
问题1. 我们学过哪些量既有大小, 又有方向?
1. 位移
如: 一个质点由A处位移到B处,
B处位于A处东偏南45?的30千米处.
·
A
45?
·
B
30 km
北
2. 力
G
重力:
方向向下,
大小m N.
F
浮力:
方向向上,
大小 a N.
还有拉力, 弹力, 摩擦力等.
3. 速度
自由落体在某时刻的速度, 物体向某个方
向运动的速度, 这些都是既有大小, 又有方向的量.
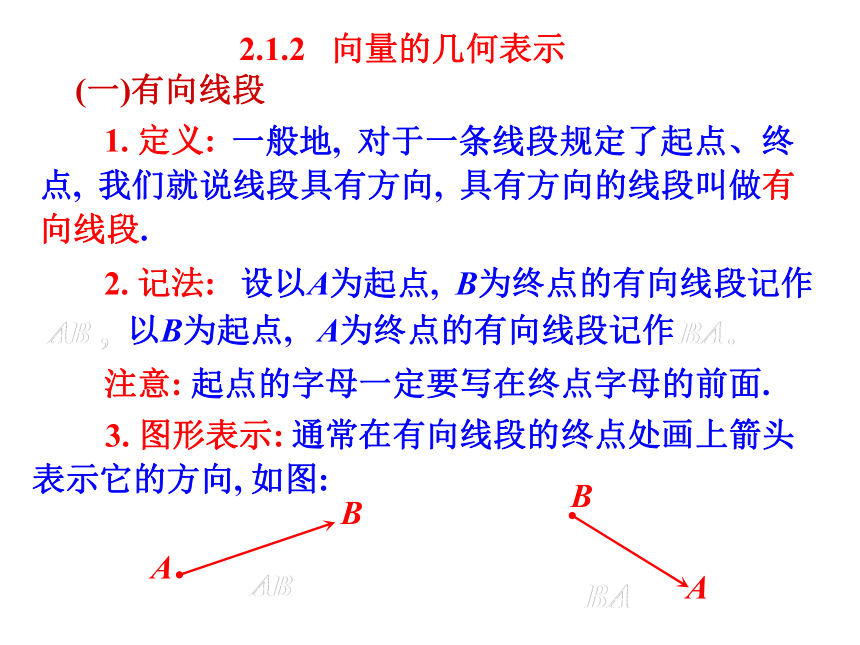
(一)有向线段
一般地, 对于一条线段规定了起点、终点, 我们就说线段具有方向, 具有方向的线段叫做有向线段.
设以A为起点, B为终点的有向线段记作
以B为起点, A为终点的有向线段记作
注意: 起点的字母一定要写在终点字母的前面.
通常在有向线段的终点处画上箭头表示它的方向, 如图:
A
B
A
B
1. 定义:
2. 记法:
3. 图形表示:
2.1.2 向量的几何表示
5. 有向线段包含三个要素:
练习(补充) 在坐标平面内画有向线段
A的坐标为(1, 0), 终点B的坐标为(4, 4).
(1)
(2)
x
y
o
1
4
4
A
B
有向线段的长度就是线段本身的长度, 用绝对值符号表示. 如
4. 长度表示:
起点、方向、长度.
答:
(1)
因为方向不同.
因为长度是相等的.
(2)
我们把既有大小, 又有方向的量叫做向量 (物理学中称为矢量); 而把只有大小, 没有方向的量称为数量, (物理学中称为标量).
向量是勾通代数, 几何, 三角函数的一种工具.
1. 向量
(二) 向量的表示
向量可用有向线段表示.
向量 的大小就是有向线段 的长度.
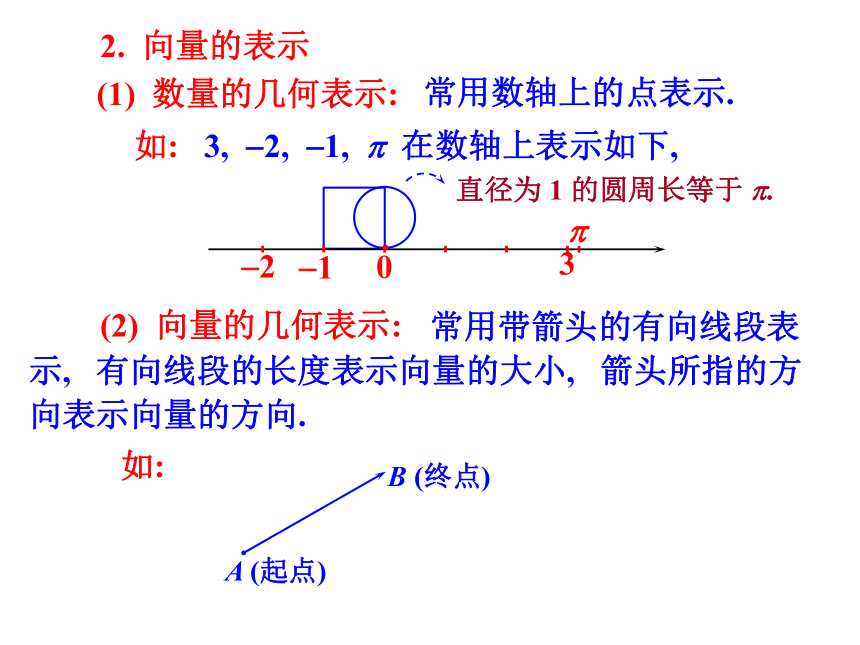
(1) 数量的几何表示:
常用带箭头的有向线段表示, 有向线段的长度表示向量的大小, 箭头所指的方向表示向量的方向.
如: 3, -2, -1, p 在数轴上表示如下,
-1
0
3
-2
p
如:
A (起点)
B (终点)
2. 向量的表示
常用数轴上的点表示.
(2) 向量的几何表示:
直径为 1 的圆周长等于 p.
① 用端点的大写字母表示, 如
② 用印刷黑体小写字母表示, 如 a、b、c.
③ 用书写体加箭头表示, 如
(3) 字母表示:
A
B
a
O
r=1
3. 向量的模:
也叫做向量的模, 记作
模为零的向量称为零向量, 记作0 ( ), 零向量的方向是任意的.
模为一个单位的向量称为单位向量.
4. 零向量:
5. 单位向量:
如图是一个单位圆,
向量 都是单位向量.
A
C
B
万
例1. 如图, 试根据图中的比例尺以及三地的位置,在图中分别用有向线段表示A地至B、C两地的位移(精确到1km).
解:
分别表示A地
到B地、C地的位移,
量得图上A、B两点
间的距离约为3cm,
A、C两点间的距离
约为3.8cm,
0.03?8000000
=240(km),
0.038?8000000
≈304(km).
练习: (课本77页)
第 1、3 题.
1. 画有向线段, 分别表示一个竖直向上、大小为18 N的力和一个水平向左、大小为28 N的力 (用1cm长表示10 N ).
0
1
3
2
18 N
0
1
3
2
28 N
A
B
C
D
画图如下:
练习: (77页)
3. 指出图中各向量的长度.
1
A
B
C
D
E
F
G
H
根据勾股定理求
解:
【课时小结】
1. 有向线段
规定了起点、终点, 我们就说线段具有方向, 具有方向的线段叫做有向线段.
起点、方向、长度是有向线段的三要素.
A
B
A
B
起点的字母一定要写在终点字母的前面.
有向线段的长度用绝对值符号表示. 如
【课时小结】
2. 向量
既有大小, 又有方向的量.
3. 向量的物理背景
位移具有方向与距离.
力具有方向与大小.
速度具有方向和大小.
向量研究具有方向和大小的问题:
【课时小结】
4. 向量的表示
向量用有向线段表示.
② 用印刷黑体小写字母表示, 如 a、b、c.
① 用端点的大写字母表示, 如
③ 用书写体加箭头表示, 如
字母表示有三种方法:
向量的大小叫做向量的模,
A
B
3
如:
用有向线段的长度表示,
【课时小结】
5. 零向量
模为零的向量称为零向量.
模为一个单位的向量称为单位向量.
零向量记作 0 ( ).
零向量的方向是任意的.
6. 单位向量
习题 2.1
第 1、2、5 题.
A 组
1. 在如图所示的坐标纸中, 用直尺和圆规画出下列向量:
(1) =4, 点A在点O正南方向;
(2) 点B在点O北偏西45?方向;
(3) =2, 点C在点O西偏南60?方向.
O
A
B
C
习题 2.1
A 组
2. 一人从 A 点出发, 向东走500米到达点B, 接着向东偏北30?走300米到达点C, 然后再向东偏北45?走100米到达点D. 试选择适当的比例尺, 用向量表示这个人的位移.
解:
北
A
B
C
D
比例尺:
100 m
向量 即是由A到D的位移.
500 m
30?
300 m
100 m
45?
5. 已知边长为 3 的等边三角形ABC, 求BC边上的中线向量 的模
A
B
D
C
解:
AB = 3, 则 BD =
由勾股定理求得
2.1.3
相等向量
与
共线向量
返回目录
学习要点
1. 什么是相等向量? 相等向量与什么有关, 与什么无关?
2. 什么叫平行向量? 什么叫共线向量? 共线向量一定画在一条直线上吗?
3. 共线向量的长度是否相等? 共线向量的方向是否相同?
2.1.3 相等向量与共线向量
长度相等, 方向相同的向量叫做相等向量, 设向量 a、b 是相等向量, 记作 a=b. 零向量与零向量是相等向量.
1. 相等向量:
如图:
解:
例2. 如图, 设O是正六边形ABCDEF的中心, 分别写出图中与向量
即: 向量与所在的位置无关.
O
A
B
C
D
E
F
x
y
O
A
B
C
D
E
F
·
·
·
·
·
·
·
练习(补充). 在平面直角坐标系中, 已知下列各点的坐标: O(0, 0), A(-1, -2), B(1, -1), C(2, 1), D(1, 2), E(-2, 2), F(-2, -1). 请找出以下向量中相等的向量.
解:
画出坐标平面上的点.
画出各向量.
相等的向量分别是:
方向相同或相反的向量叫做平行向量, 设 是平行向量,
一组平行向量称为共线向量. 因为决定向量的两个要素是模和方向, 与位置无关, 即任一组平行向量都可以移到与它们平行的一条直线上.
2. 平行向量与共线向量:
例(补充). 如图, D、E、F 分别是△ABC各边中点, 图中哪些线段所确定的向量与向量 共线?
A
B
C
D
E
F
答:
图中与 共线的有:
x
y
O
A
B
C
D
E
F
·
·
·
·
·
·
·
练习(补充). 在平面直角坐标系中, 已知下列各点的坐标: O(0, 0), A(-1, -2), B(1, -1), C(2, 1), D(1, 2), E(-1, 1), F(-2, -1). 以下向量哪些是共线向量.
解:
画出坐标平面上的点.
画出各向量.
共线向量分别是:
练习: (课本77页)
第 2、4 题.
2. 非零向量 AB 的长度怎样表示? 非零向量 BA的长度怎样表示? 这两个向量的长度相等吗? 这两个向量相等吗?
答: 的长度表示为
的长度表示为
这两个相量的长度相等;
这两个是非零向量, 方向相反, 两向量不等.
4. (1) 用有向线段表示两个相等的向量, 如果有相同的起点, 那么它们的终点是否相同?
(2) 用有向线段表示两个方向相同但长度不同的向量, 如果有相同的起点, 那么它们的终点是否相同?
答: (1) 两向量相等, 若起点相同, 终点一定相同.
(2) 两向量方向相同而长度不同, 则两向量不等, 若这两向量起点相同, 则终点一定不同.
【课时小结】
1. 相等向量
长度相等, 方向相同的向量叫做相等向量.
相等向量与长度和方向都有关.
相等向量与位置无关.
2. 共线向量
方向相同或相反的向量叫做平行向量.
一组平行向量称为共线向量.
共线向量与长度和位置无关.
共线向量与方向有关, 同方向或反方向.
习题 2.1
第 3、4、6 题.
A 组
B 组
第 1、2 题.
3. 如图, D、E、F 分别是△ABC各边的中点, 写出图中与
解:
A
B
C
D
E
F
习题 2.1
A 组
解:
4. 如图, 在方格纸上的□ ABCD和折线MPQRST中, 点O是□ABCD对角线的交点, 且
分别写出图中与 相等的向量.
A
B
C
D
M
P
Q
R
S
T
O
6. 判断下列结论是否正确(正确的在括号内打“√”, 错误的打“×”), 并说明理由:
(1) 若 a、b 都是单位向量, 则 a=b. ( )
(2) 物理学中的作用力与反作用力是一对共线向量. ( )
(3) 方向为南偏西60?的向量与北偏东60?的向量是共线向量. ( )
(4) 直角坐标平面上的 x 轴、y 轴是向量. ( )
解:
(1)
错,
因为向量 与 的方向可能不同.
(2)
对,
因为作用力和反作用力是方向相反的.
(3)
60?
60?
对,
如图,
(4)
错,
x 轴, y 轴不是线段.
两向量的方向相反.
1. 有人说, 由于海平面以上的高度(海拔)用正数表示, 海平面以下的高度用负数表示, 所以海拔也是向量.你同意他的看法吗? 温度、角度是向量吗? 为什么?
答: 海拔不是向量, 它只是相对于海平面上下高度的一个量, 它只有空间高度, 不具有起点和终点, 不表示海平面上下以外的任意方向.
同样, 温度、角度也不是向量.
B 组
2. 在矩形ABCD中, AB=2BC, M、N分别是AB、CD的中点, 在以A、B、C、D、M、N为起点和终点的所有向量中, 相等向量共有多少对?
解:
A
B
C
D
M
N
与向量 相等的有
6对;
反方向又有 6 对;
2 对;
3 对;
其反方向又有 3 对;
2 对;
2 对;
共 24 对.
如图,
水平方向还有
竖直方向有
对角线方向有
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
2.1
平面向量的实际背景
及基本概念
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
2.1.1
2.1.2
向量的物理背景与概念
向量的几何表示
返回目录
学习要点
1. 什么是有向线段? 有向线段包含哪三个要素? 有向线段的记法和图形表示是怎样的?
2. 什么是向量? 它由几个要素构成?
3. 向量的几何表示与字母表示分别是怎样的?
4. 什么是零向量? 什么是单位向量? 零向量是怎样表示的?
5. 什么是向量的模? 它是怎样表示法?
2.1.1 向量的物理背景与概念
问题1. 我们学过哪些量既有大小, 又有方向?
1. 位移
如: 一个质点由A处位移到B处,
B处位于A处东偏南45?的30千米处.
·
A
45?
·
B
30 km
北
2. 力
G
重力:
方向向下,
大小m N.
F
浮力:
方向向上,
大小 a N.
还有拉力, 弹力, 摩擦力等.
3. 速度
自由落体在某时刻的速度, 物体向某个方
向运动的速度, 这些都是既有大小, 又有方向的量.
(一)有向线段
一般地, 对于一条线段规定了起点、终点, 我们就说线段具有方向, 具有方向的线段叫做有向线段.
设以A为起点, B为终点的有向线段记作
以B为起点, A为终点的有向线段记作
注意: 起点的字母一定要写在终点字母的前面.
通常在有向线段的终点处画上箭头表示它的方向, 如图:
A
B
A
B
1. 定义:
2. 记法:
3. 图形表示:
2.1.2 向量的几何表示
5. 有向线段包含三个要素:
练习(补充) 在坐标平面内画有向线段
A的坐标为(1, 0), 终点B的坐标为(4, 4).
(1)
(2)
x
y
o
1
4
4
A
B
有向线段的长度就是线段本身的长度, 用绝对值符号表示. 如
4. 长度表示:
起点、方向、长度.
答:
(1)
因为方向不同.
因为长度是相等的.
(2)
我们把既有大小, 又有方向的量叫做向量 (物理学中称为矢量); 而把只有大小, 没有方向的量称为数量, (物理学中称为标量).
向量是勾通代数, 几何, 三角函数的一种工具.
1. 向量
(二) 向量的表示
向量可用有向线段表示.
向量 的大小就是有向线段 的长度.
(1) 数量的几何表示:
常用带箭头的有向线段表示, 有向线段的长度表示向量的大小, 箭头所指的方向表示向量的方向.
如: 3, -2, -1, p 在数轴上表示如下,
-1
0
3
-2
p
如:
A (起点)
B (终点)
2. 向量的表示
常用数轴上的点表示.
(2) 向量的几何表示:
直径为 1 的圆周长等于 p.
① 用端点的大写字母表示, 如
② 用印刷黑体小写字母表示, 如 a、b、c.
③ 用书写体加箭头表示, 如
(3) 字母表示:
A
B
a
O
r=1
3. 向量的模:
也叫做向量的模, 记作
模为零的向量称为零向量, 记作0 ( ), 零向量的方向是任意的.
模为一个单位的向量称为单位向量.
4. 零向量:
5. 单位向量:
如图是一个单位圆,
向量 都是单位向量.
A
C
B
万
例1. 如图, 试根据图中的比例尺以及三地的位置,在图中分别用有向线段表示A地至B、C两地的位移(精确到1km).
解:
分别表示A地
到B地、C地的位移,
量得图上A、B两点
间的距离约为3cm,
A、C两点间的距离
约为3.8cm,
0.03?8000000
=240(km),
0.038?8000000
≈304(km).
练习: (课本77页)
第 1、3 题.
1. 画有向线段, 分别表示一个竖直向上、大小为18 N的力和一个水平向左、大小为28 N的力 (用1cm长表示10 N ).
0
1
3
2
18 N
0
1
3
2
28 N
A
B
C
D
画图如下:
练习: (77页)
3. 指出图中各向量的长度.
1
A
B
C
D
E
F
G
H
根据勾股定理求
解:
【课时小结】
1. 有向线段
规定了起点、终点, 我们就说线段具有方向, 具有方向的线段叫做有向线段.
起点、方向、长度是有向线段的三要素.
A
B
A
B
起点的字母一定要写在终点字母的前面.
有向线段的长度用绝对值符号表示. 如
【课时小结】
2. 向量
既有大小, 又有方向的量.
3. 向量的物理背景
位移具有方向与距离.
力具有方向与大小.
速度具有方向和大小.
向量研究具有方向和大小的问题:
【课时小结】
4. 向量的表示
向量用有向线段表示.
② 用印刷黑体小写字母表示, 如 a、b、c.
① 用端点的大写字母表示, 如
③ 用书写体加箭头表示, 如
字母表示有三种方法:
向量的大小叫做向量的模,
A
B
3
如:
用有向线段的长度表示,
【课时小结】
5. 零向量
模为零的向量称为零向量.
模为一个单位的向量称为单位向量.
零向量记作 0 ( ).
零向量的方向是任意的.
6. 单位向量
习题 2.1
第 1、2、5 题.
A 组
1. 在如图所示的坐标纸中, 用直尺和圆规画出下列向量:
(1) =4, 点A在点O正南方向;
(2) 点B在点O北偏西45?方向;
(3) =2, 点C在点O西偏南60?方向.
O
A
B
C
习题 2.1
A 组
2. 一人从 A 点出发, 向东走500米到达点B, 接着向东偏北30?走300米到达点C, 然后再向东偏北45?走100米到达点D. 试选择适当的比例尺, 用向量表示这个人的位移.
解:
北
A
B
C
D
比例尺:
100 m
向量 即是由A到D的位移.
500 m
30?
300 m
100 m
45?
5. 已知边长为 3 的等边三角形ABC, 求BC边上的中线向量 的模
A
B
D
C
解:
AB = 3, 则 BD =
由勾股定理求得
2.1.3
相等向量
与
共线向量
返回目录
学习要点
1. 什么是相等向量? 相等向量与什么有关, 与什么无关?
2. 什么叫平行向量? 什么叫共线向量? 共线向量一定画在一条直线上吗?
3. 共线向量的长度是否相等? 共线向量的方向是否相同?
2.1.3 相等向量与共线向量
长度相等, 方向相同的向量叫做相等向量, 设向量 a、b 是相等向量, 记作 a=b. 零向量与零向量是相等向量.
1. 相等向量:
如图:
解:
例2. 如图, 设O是正六边形ABCDEF的中心, 分别写出图中与向量
即: 向量与所在的位置无关.
O
A
B
C
D
E
F
x
y
O
A
B
C
D
E
F
·
·
·
·
·
·
·
练习(补充). 在平面直角坐标系中, 已知下列各点的坐标: O(0, 0), A(-1, -2), B(1, -1), C(2, 1), D(1, 2), E(-2, 2), F(-2, -1). 请找出以下向量中相等的向量.
解:
画出坐标平面上的点.
画出各向量.
相等的向量分别是:
方向相同或相反的向量叫做平行向量, 设 是平行向量,
一组平行向量称为共线向量. 因为决定向量的两个要素是模和方向, 与位置无关, 即任一组平行向量都可以移到与它们平行的一条直线上.
2. 平行向量与共线向量:
例(补充). 如图, D、E、F 分别是△ABC各边中点, 图中哪些线段所确定的向量与向量 共线?
A
B
C
D
E
F
答:
图中与 共线的有:
x
y
O
A
B
C
D
E
F
·
·
·
·
·
·
·
练习(补充). 在平面直角坐标系中, 已知下列各点的坐标: O(0, 0), A(-1, -2), B(1, -1), C(2, 1), D(1, 2), E(-1, 1), F(-2, -1). 以下向量哪些是共线向量.
解:
画出坐标平面上的点.
画出各向量.
共线向量分别是:
练习: (课本77页)
第 2、4 题.
2. 非零向量 AB 的长度怎样表示? 非零向量 BA的长度怎样表示? 这两个向量的长度相等吗? 这两个向量相等吗?
答: 的长度表示为
的长度表示为
这两个相量的长度相等;
这两个是非零向量, 方向相反, 两向量不等.
4. (1) 用有向线段表示两个相等的向量, 如果有相同的起点, 那么它们的终点是否相同?
(2) 用有向线段表示两个方向相同但长度不同的向量, 如果有相同的起点, 那么它们的终点是否相同?
答: (1) 两向量相等, 若起点相同, 终点一定相同.
(2) 两向量方向相同而长度不同, 则两向量不等, 若这两向量起点相同, 则终点一定不同.
【课时小结】
1. 相等向量
长度相等, 方向相同的向量叫做相等向量.
相等向量与长度和方向都有关.
相等向量与位置无关.
2. 共线向量
方向相同或相反的向量叫做平行向量.
一组平行向量称为共线向量.
共线向量与长度和位置无关.
共线向量与方向有关, 同方向或反方向.
习题 2.1
第 3、4、6 题.
A 组
B 组
第 1、2 题.
3. 如图, D、E、F 分别是△ABC各边的中点, 写出图中与
解:
A
B
C
D
E
F
习题 2.1
A 组
解:
4. 如图, 在方格纸上的□ ABCD和折线MPQRST中, 点O是□ABCD对角线的交点, 且
分别写出图中与 相等的向量.
A
B
C
D
M
P
Q
R
S
T
O
6. 判断下列结论是否正确(正确的在括号内打“√”, 错误的打“×”), 并说明理由:
(1) 若 a、b 都是单位向量, 则 a=b. ( )
(2) 物理学中的作用力与反作用力是一对共线向量. ( )
(3) 方向为南偏西60?的向量与北偏东60?的向量是共线向量. ( )
(4) 直角坐标平面上的 x 轴、y 轴是向量. ( )
解:
(1)
错,
因为向量 与 的方向可能不同.
(2)
对,
因为作用力和反作用力是方向相反的.
(3)
60?
60?
对,
如图,
(4)
错,
x 轴, y 轴不是线段.
两向量的方向相反.
1. 有人说, 由于海平面以上的高度(海拔)用正数表示, 海平面以下的高度用负数表示, 所以海拔也是向量.你同意他的看法吗? 温度、角度是向量吗? 为什么?
答: 海拔不是向量, 它只是相对于海平面上下高度的一个量, 它只有空间高度, 不具有起点和终点, 不表示海平面上下以外的任意方向.
同样, 温度、角度也不是向量.
B 组
2. 在矩形ABCD中, AB=2BC, M、N分别是AB、CD的中点, 在以A、B、C、D、M、N为起点和终点的所有向量中, 相等向量共有多少对?
解:
A
B
C
D
M
N
与向量 相等的有
6对;
反方向又有 6 对;
2 对;
3 对;
其反方向又有 3 对;
2 对;
2 对;
共 24 对.
如图,
水平方向还有
竖直方向有
对角线方向有
