2020-2021学年高一数学人教A版必修4第二章2.3 平面向量的基本定理及坐标表示4课时课件(共97张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第二章2.3 平面向量的基本定理及坐标表示4课时课件(共97张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 21:35:26 | ||
图片预览








文档简介
第二章
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
平面向量的基本定理
及
2.3
坐标表示
2.3.1 平面向量基本定理
复习与提高
2.3.2 平面向量坐标表示
2.3.3 平面向量坐标运算
2.3.4 平面向量共线的坐标表示
2.3.1
平面向量基本定理
返回目录
学习要点
1. 什么叫基底? 基底有什么特性? 基底的作用是什么?
2. 平面内任一向量如何用基底表示?
3. 向量的夹角是指什么样的角? 它在什么范围内?
操作题: 任画不共线的两向量 e1、e2 和另一向量 a, 作图: 用 e1、e2 的向量数乘之和表示 a .
(1)
O
A
(2)
B
(3)
C
(4)
使点E在OB上,
(5)
E
取一个实数l1,
平面向量基本定理: 如果 e1、e2 是同一平面内的两个不共线向量, 那么对于这一平面内的任一向量 a, 有且只有一对实数 l1、l2, 使
a = l1e1+l2e2.
即: 平面内任一向量 a, 可用平面内不共线的两向量 e1、e2表示. e1、e2叫做表示平面内所有向量的一组基底.
(一)基本定理
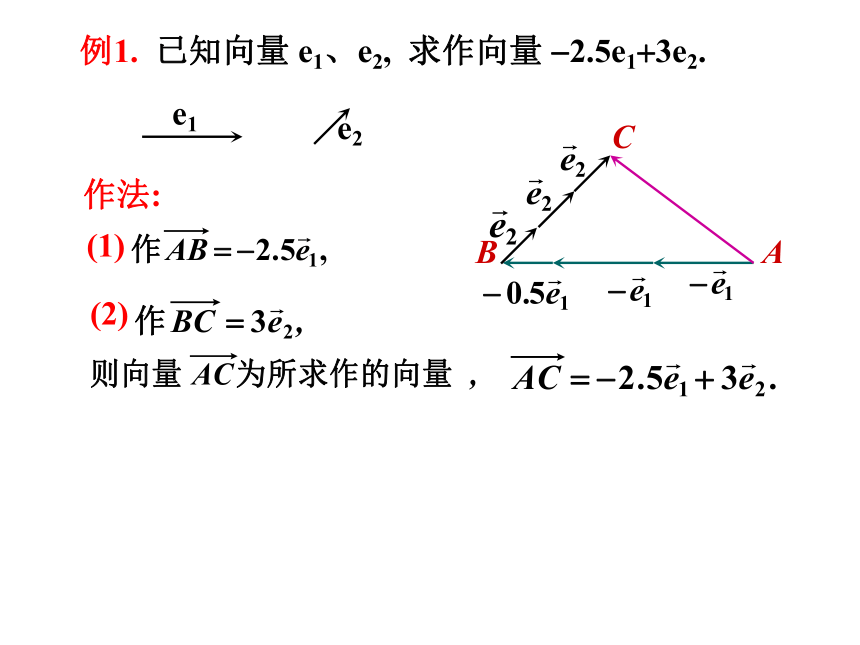
例1. 已知向量 e1、e2, 求作向量 -2.5e1+3e2.
A
B
C
e1
e2
作法:
(1)
(2)
练习: (补充)
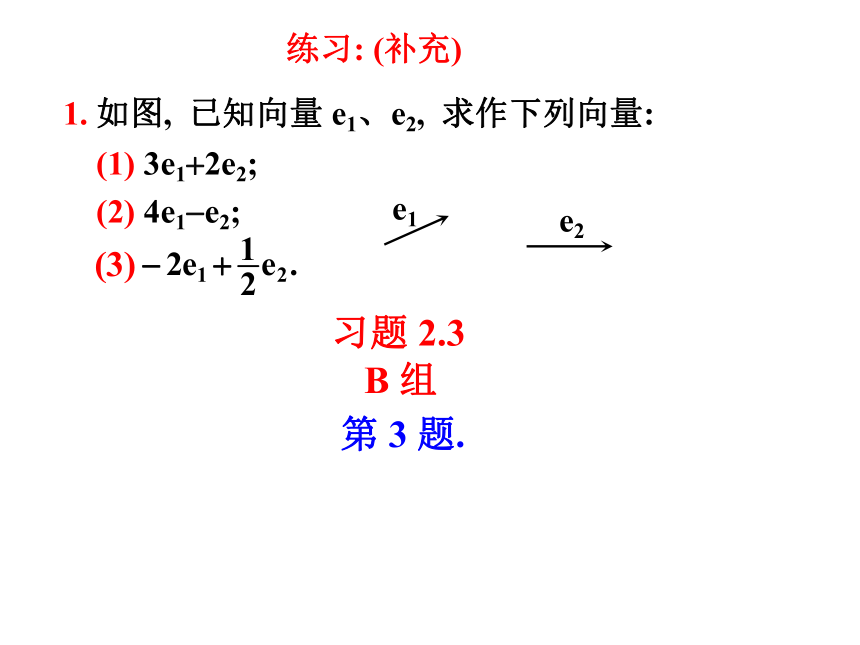
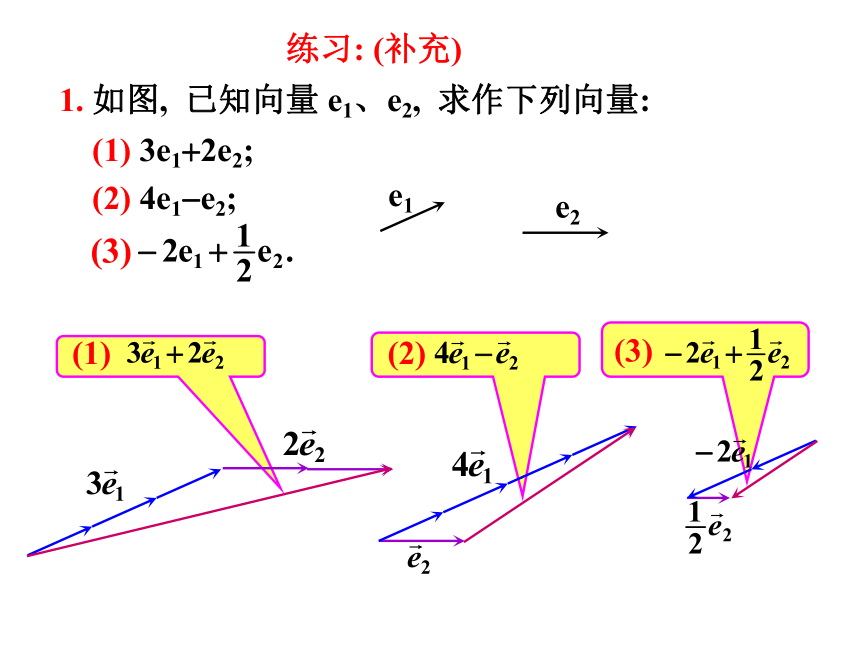
1. 如图, 已知向量 e1、e2, 求作下列向量:
(1) 3e1+2e2;
(2) 4e1-e2;
(3)
e1
e2
习题 2.3
B 组
第 3 题.
1. 如图, 已知向量 e1、e2, 求作下列向量:
(1) 3e1+2e2;
(2) 4e1-e2;
(3)
e1
e2
(1)
(2)
(3)
练习: (补充)
3. 设 e1、e2 是平面内一组基底, 证明: 当
l1e1+l2e2=0
时, 恒有
l1=l2=0.
证明:
假设 l1≠0, l2≠0,
则 l1e1+l2e2=0 可变为
于是得 共线,
而 是一组基底, 不能共线.
∴假设不成立, 则 l1=l2=0成立.
习题 2.3
B 组
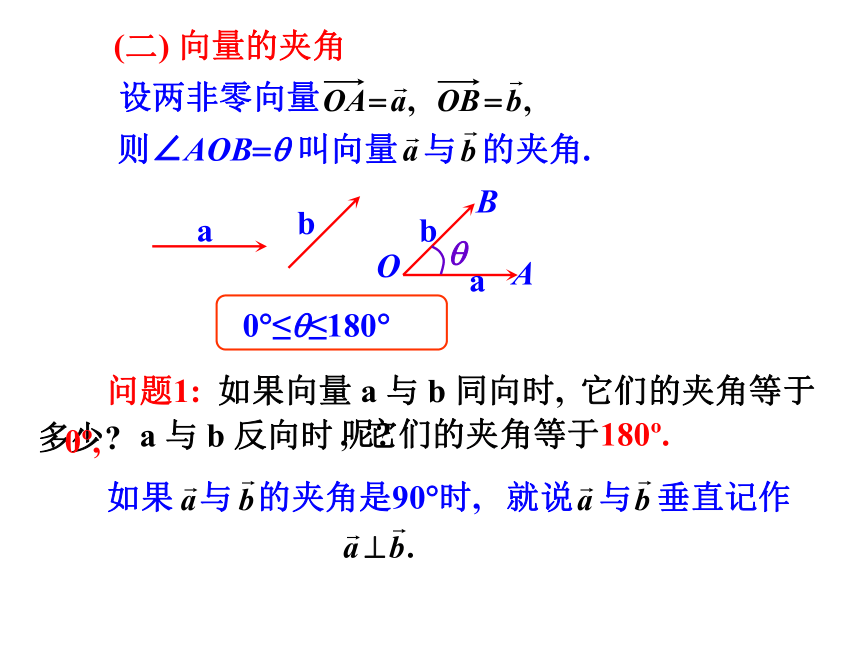
(二) 向量的夹角
设两非零向量
则∠AOB=q 叫向量 与 的夹角.
0?≤q≤180?
如果 与 的夹角是90?时, 就说 与 垂直记作
a
b
a
b
O
A
B
q
问题1: 如果向量 a 与 b 同向时, 它们的夹角等于
a 与 b 反向时
多少?
呢?
0?,
, 它们的夹角等于180?.
问题2: 下面标注的角中, 哪些角等于向量 a 与 b的夹角?
①
②
③
④
⑤
a
b
a
b
a
b
a
b
a
b
b
a
b
b
b
标注的角等于向量 a 与 b 的夹角的有
①
④
②③⑤中, 标注的角与向量 a 与 b 的夹角互补.
问题3. 在等边三角形ABC中, D是BC的中点.
(1) 向量 与 的夹角是多少?
(2) 向量 与 的夹角是多少?
(3) 向量 与 的夹角是多少?
(4) 向量 与 的夹角是多少?
A
B
C
D
60?
30?
90?
120?
练习(补充)
1. 设非零向量 a, b, c, 满足 |a|=|b|=|c|, a+b=c,则 a 与 b 的夹角等于 ( )
(A) 150? (B) 120? (C) 60? (D) 30?
2. 平面向量 a 与 b 的夹角为 60?, |a|=2, |b|=1,则 |a+2b| 的模等于 ( )
(A) (B) (C) 4 (D) 12
1. 设非零向量 a, b, c, 满足 |a|=|b|=|c|, a+b=c,则 a 与 b 的夹角等于 ( )
(A) 150? (B) 120? (C) 60? (D) 30?
解:
由三角形法则作 a+b=c,
由 |a|=|b|=|c| 得三角形是等边三角形.
得 a 与 b 的夹角应是
B
120?.
2. 平面向量 a 与 b 的夹角为 60?, |a|=2, |b|=1,则 |a+2b| 的模等于 ( )
(A) (B) (C) 4 (D) 12
解:
画出 a 与 b 的夹角为 60?, |a|=2, |b|=1.
60?
再由平行四边形法则画 a+2b,
A
B
C
D
在△ABC 中可求得
B
【课时小结】
1. 向量基本定理
平面内任一向量 a, 都可用平面内不共线的两向量 e1、e2 的数乘的和表示, 即
e1、e2 称为一组基底.
a = l1e1+l2e2 (l1, l2?R).
【课时小结】
2. 两向量的夹角
0?≤q≤180?.
a
b
a
b
O
A
B
q
起点重合时的两向量的夹角,
范围是 [0?, 180?].
练习: (补充)
1. 在△ABC中, D是AB上的点, 且AD:DB=1:2, 设 用 表示
O
A
B
C
2. 如图, 是单位向量, 且
与 的夹角为30?,
试用 表示
3. 在△ABC中, 作
AE、EF分别是△ABC的什么线?
4. 已知单位向量 a⊥b, 向量 c 满足 a-c⊥b-c, 则 |c| 的最大值等于多少?
1. 在△ABC中, D是AB上的点, 且AD:DB=1:2, 设 用 表示
A
C
B
D
解:
由 AD:DB=1:2 得
如图,
O
A
B
C
2. 如图, 是单位向量, 且 与 的夹角为30?, 试用 表示
解:
作CD⊥OB (延长线) 于D,
D
在Rt△CDO中, 由已知得
OC=2, ∠COD=30?,
∴CD=1,
则
3. 在△ABC中, 作
AE、EF分别是△ABC的什么线?
A
C
B
E
M
作法:
① 取AB的中点M,
F
则ME为△ABC的中位线,
作ME//AC, 交BC于E,
② 作EF//BA, 交AC于F,
得
∴ 为所求.
则
答: AE是△ABC的中线, EF是一条中位线.
4. 已知单位向量 a⊥b, 向量 c 满足 a-c⊥b-c, 则 |c| 的最大值等于多少?
解:
如图, 单位向量 a⊥b,
要作 a-c, b-c,
向量减法, 起点重合.
作出 a-c, b-c.
∵a⊥b, a-c⊥b-c,
A
B
∴向量 c 的终点 C 在以 AB 为直径的圆上.
C
则 |c| 最大时是这个圆的直径.
∵a, b 是单位向量,
则
2.3.2
平面向量的正交分解
2.3.3
平面向量的坐标运算
及坐标表示
返回目录
学习要点
1. 什么叫正交分解?
2. 直角坐标平面内的向量是以什么作为一组基底的?
3. 向量的坐标是怎样确定的? 两向量相等时, 坐标有什么关系?
4. 向量的坐标运算法则是怎样的?
2.3.2 平面向量的正交分解及坐标表示
为了借助于坐标平面研究向量, 需要把一个向量分解成两个互相垂直的向量.
把一个向量分解为两个互相垂直的向量, 叫做把向量正交分解.
(一) 向量的正交分解
在物理学中, 我们学过力的分解与合成.
同样, 我们也可以对平面向量进行分解.
如图:
将向量 分解成水平和竖直的两个向量.
O
A
B
C
(二) 向量的坐标表示
在平面直角坐标系中, 分别取 x 轴、y 轴方向的单位向量 i、j 作为一组基底.
根据向量基本定理, 坐标平面内的任一向量 a 都可用向量 i、j 表示.
x
y
o
i
j
a
b
4i
2j
3i
-6j
的坐标表示为:
图中向量
如图:
定义: 在直角坐标系内, 取 x 轴、 y 轴方向的一组单位向量 i、j 为基底, 任一向量 a 唯一存在一对实数 x、y, 使得
a = xi+yj
我们把 (x, y) 叫做向量 a 的坐标, 记作
a = (x, y),
这种表示叫做向量的坐标表示.
显然, i = (1, 0), j = (0, 1),
若 a=(x1, y1), b=(x2, y2), 当且仅当
时 a=b.
例2. 如图, 分别用基底 i、j 表示向量 a、b、c, 并写出它们的坐标.
x
y
o
i
j
解:
= (2, 3).
= (5, 0).
= (-5, 1).
练习: (补充)
1. 如图, 分别用基底 i、j 表示向量 a、b、c、d、e、f, 并写出它们的坐标.
i
1
2
3
4
-1
-2
-3
-4
-5
1
2
3
4
5
-1
-2
-3
-4
x
y
o
j
A
A1
A2
解:
= (2, 3).
= (2, 3).
= (-2, 3).
= (-2, -3).
= (4, -2).
= (2, -3).
问题1: 设向量 a = ( x1, y1 ), b = ( x2, y2 ), 则a+b = ( x1+x2, y1+y2 ) 是否成立? la=(lx1, ly1) 是否成立? 为什么?
2.3.3 平面向量的坐标运算
答: 上述结论成立.
结论:
两个向量和 ( 差 ) 的坐标分别等于这两个向量相应坐标的和 ( 差 ).
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
例4. 已知 a=(2, 1), b=(-3, 4), 求 a+b, a-b, 3a+4b 的坐标.
解:
= (-1, 5);
= (5, -3);
= (6, 3) + (-12, 16)
= (-6, 19).
2. 已知 a=(3, 2), b=(0, -1), 求 -2a+4b, 4a+3b 的坐标.
解:
= (-6, -4) + (0, -4)
= (-6, -8);
= (12, 8) + (0, -3)
= (12, 5).
练习: (课本100页)
问题:
B 的坐标就是 (5, 2) 吗? 如果起点A的坐标是 (-2, -3), 画图看看, 终点B的坐标应该是多少?
x
y
o
B
A
B
A
A
B
A
B
A
B
(3, -1)
(5, 2)
终点 B 的坐标就不是(5, 2).
如果起点 A 不在原点,
如果起点A(-2, -3),
终点B(3, -1).
如果起点在原点,
则终点为
-2
-3
B(5, 2).
5
2
例3. 已知 O 为原点, 点 A、B 的坐标为A(x1, y1), B(x2, y2),
解:
由 A(x1, y1), B(x2, y2) 得
结论: 一个向量的坐标等于这个向量的终点坐标减去起点坐标.
x
o
y
A
B
C
D
-2
3
1
4
例5. 如图, 已知□ABCD的三个顶点A、B、C 的坐标分别是 (-2, 1) 、 (-1, 3) 、 (3, 4), 试求顶点 D的坐标.
解:
在□ABCD中,
(-1+2,
3-1)
=(1, 2),
设点 D(x, y),
则
(3-x,
4-y),
由 得
(1, 2) = (3-x, 4-y),
得
解得
∴顶点 D 的坐标是(2, 2).
x
o
y
A
B
C
D
-2
3
1
4
例5. 如图, 已知□ABCD的三个顶点A、B、C 的坐标分别是 (-2, 1) 、 (-1, 3) 、 (3, 4), 试求顶点 D的坐标.
解:
法二,
+(4, 1)
= (3, -1),
= (-1, -2)
设点 D(x, y),
由 的和向量表示:
而 的坐标等于终点坐标减起点坐标,
即(3, -1) = (x+1, y-3),
得
解得
∴顶点 D 的坐标是(2, 2).
练习: (课本100页)
第 1、3 题.
1. 已知向量 a, b 的坐标, 求 a+b, a-b 的坐标.
(1) a=(-2, 4), b=(5, 2); (2) a=(4, 3), b=(-3, 8);
(3) a=(2, 3), b=(-2, -3); (4) a=(3, 0), b=(0, 4).
解: (1)
(2)
(3)
(4)
= (3, 6);
= (-7, 2).
= (1, 11);
= (7, -5).
= (0, 0);
= (4, 6).
= (3, 4);
= (3, -4).
练习: (课本100页)
3. 已知A、B两点的坐标, 求 的坐标.
(1) A(3, 5), B(6, 9); (2) A(-3, 4), B(6, 3);
(3) A(0, 3), B(0. 5); (4) A(3. 0), B(8, 0).
解: (1)
= (3, 4);
= (-3, -4).
= (9, -1);
= (-9, 1).
= (0, 2);
= (0, -2).
= (5, 0);
= (-5, 0).
(2)
(3)
(4)
【课时小结】
1. 向量的正交分解
把一个向量分解为两个互相垂直的向量, 叫做把向量正交分解.
O
A
B
C
x
y
o
a
x
y
a=x+y.
【课时小结】
2. 向量的坐标表示
在平面直角坐标系中, 分别取 x 轴、y 轴方向的单位向量 i、j 作为一组基底, 对坐标平面内的任一向量 a 作正交分解,
如图, 正交分解向量 a
(x, y) 叫做向量 a 的坐标, 记作
a = xi+yj
x
y
O
a = (x, y).
向量 a 的坐标表示
【课时小结】
3. 向量的坐标运算
A(x1, y1), B(x2, y2)
(1)
(2)
(3)
若 a=(x1, y1), b=(x2, y2), 当且仅当
时 a=b.
习题2.3
第 1、2、3、4 题.
A 组
第 1 题.
B 组
解:
设终点B的坐标为(x, y),
(1)
=(-2, 1),
? x= -2, y=1,
∴终点 B 的坐标为(-2, 1);
(2)
=(1, 3),
得 x+1=1, y-5=3,
∴终点 B 的坐标为(0, 8);
解得 x=0, y=8,
(3)
=(-2, -5)
得 x-3= -2, y-7= -5,
∴终点 B 的坐标为(1, 2).
解得 x=1, y=2,
1. 已知表示向量 a 的有向线段始点 A 的坐标, 求它的终点 B 的坐标:
(1) a=(-2, 1), A(0, 0); (2) a=(1, 3), A(-1, 5);
(3) a=(-2, -5), A(3, 7).
习题2.3
A 组
解:
∵三个力都作用在坐标原点,
∴F1+F2+F3= (3, 4) + (2, -5) + (3, 1)
= (8, 0).
2. 已知作用在坐标原点的三个力F1=(3, 4), F2=(2, -5), F3=(3, 1), 求作用在原点的合力F1+F2+F3的坐标.
解:
设点 D 的坐标为(x, y),
= (2, 7),
= ( x+1, y+2 ),
∴有 x+1=2, y+2=7,
解得 x=1, y=5,
∴点 D 的坐标为(1, 5).
3. 已知□ABCD的顶点 A(-1, -2), B(3, -1), C(5, 6), 求顶点 D 的坐标.
4. 已知点A(1, 1), B(-1, 5)及
求点 C、D、E 的坐标.
解:
(-1-1, 5-1)
=(-2, 4),
设 C(x1, y1) 、D(x2, y2) 、E(x3, y3),
① 由 得
(x1-1, y1-1)= (-2, 4),
得
解得 x1=0, y1=3,
?C(0, 3).
② 由 得
(x2-1, y2-1)=2(-2, 4),
得
解得 x2= -3, y2=9,
?D(-3, 9).
③ 由 得
(x3-1, y3-1)= (-2, 4),
得
解得 x3=2, y3= -1,
?E(2, -1).
解:
=(3, 3),
当t =1时,
=(1, 2) + (3, 3)
=(4, 5),
当t= -2时,
=(1, 2) -2(3, 3)
=(-5, -4),
当t =2时,
=(1, 2)+2(3, 3)
=(7, 8),
1. 已知点O(0, 0), A(1, 2), B(4, 5),
当 t=1, -2, 2时, 分别求点 P 的坐标.
由已知得
得P点的坐标为(4, 5).
得P点的坐标为(-5, -4).
得P点的坐标为
得P点的坐标为(7, 8).
B 组
2.3.4
平面向量共线
的坐标表示
返回目录
学习要点
1. 用坐标表示向量时, 两向量共线的条件是什么?
2. 怎样用向量的坐标求线段分点的坐标?
问题1. 两非零向量 共线的条件是什么? 试推导一下, 它们的坐标存在什么关系?
答: 当且仅当存在实数l, 使
则 与 共线.
设
则 (x1, y1) = l(x2, y2),
得
消去l得 x1y2-x2y1=0.
或
x1y2=x2y1
结论: 两非零向量共线, 其 x、y 坐标交叉相乘相等.
坐标关系:
(一) 向量共线的坐标表示
例6. 已知 a=(4, 2), b=(6, y), 且a∥b, 求 y.
解:
∴4y-2?6=0,
解得 y=3.
例7. 已知A(-1, -1), B(1, 3), C(2, 5), 试判断A, B, C 三点之间的位置关系.
解:
= (2, 4),
= (1, 2),
又 2?2 - 4?1 = 0.
∴A, B, C 三点在一条直线上.
分析:
则考虑共点的两向量是否共线.
∴ 与 共线,
而 与 共点B,
x
y
o
A
B
C
·
·
·
-1
-1
1
3
2
5
如图,
A、B、C 三点共线,
观察估计,
练习:
A 组
习题 2.3
第 5、6 题.
解:
解得 x = -4,
5. x 为何值时, a=(2, 3) 与 b=(x, -6) 共线?
若 共线,
则2?(-6)-3x=0,
即 x= -4 时 与 共线.
A 组
习题 2.3
解:
而 4(-8) - 4(-8) = 0,
6. 已知A(-2, -3), B(2, 1), C(1, 4), D(-7, -4), 试问 与 是否共线?
由题设得
(二) 线段的分点
例8. 设点 P 是线段P1P2上的一点, P1、P2的坐标分别是 (x1, y1), (x2, y2).
(1) 当点 P 是线段 P1P2 的中点时, 求点 P 的坐标;
(2) 当点 P 是线段 P1P2 的一个三等分点时, 求点 P 的坐标.
解:
(1)
∵P 是线段 P1P2 的中点
设 P 点的坐标为 P(x, y),
则 (x-x1, y-y1) = (x2-x, y2-y),
即
得线段中点的坐标公式:
(二) 线段的分点
例8. 设点 P 是线段P1P2上的一点, P1、P2的坐标分别是 (x1, y1), (x2, y2).
(1) 当点 P 是线段 P1P2 的中点时, 求点 P 的坐标;
(2) 当点 P 是线段 P1P2 的一个三等分点时, 求点 P 的坐标.
解:
(2)
同理, 设 P(x, y),
若
P1
P2
P
则 (x-x1, y-y1) = (x2-x, y2-y),
若
P1
P2
P
练习: (课本100页)
第 5、6 题.
练习: (补充)
设P1、P2的坐标分别是(x1, y1), (x2, y2). 点 P 是直线P1P2上的一点, 若 求点 P 的坐标.
5. 求线段 AB 的中点坐标:
(1) A(2, 1), B(4, 3);
(2) A(-1, 2), B(3, 6);
(3) A(5, -4), B(3, -6).
解:
(1)
=3,
=2,
∴AB 中点的坐标是(3, 2).
(2)
同(1)得x=1,
y=4,
∴AB 中点的坐标是(1, 4).
(3)
x=4,
y= -5,
∴AB 中点的坐标是(4, -5).
6. 已知向量 =(2, 3), =(6, -3), 点 P 是线段 AB 的三等分点, 求点 P 的坐标.
解:
由 得
点A(2, 3), B(6, -3).
设两个三等分点分别为(x1, y1), (x2, y2),
则
=1,
= -1,
∴两个三等分点分别为( 1), ( -1).
练习: (补充)
设P1、P2的坐标分别是(x1, y1), (x2, y2). 点 P 是直线P1P2上的一点, 若 求点 P 的坐标.
解:
设 P 点的坐标为 P(x, y),
则 (x-x1, y-y1) = l(x2-x, y2-y),
得
结论:
P1(x1, y1), P2(x2, y2), P(x, y) 分P1P2为
则
分点坐标
公式
【课时小结】
1. 向量共线的坐标表示
设
两向量共线, 其 x、y 坐标交叉相乘相等.
若 x1y2-x2y1=0, 则 与 共线.
【课时小结】
2. 线段的分点坐标
设 P(x, y), P1(x1, y1), P2(x2, y2),
(1) 若 P 是 P1P2 的中点, 则
(2) 若 则
A 组
习题 2.3
练习: (课本100页)
第 4、7 题.
第 7 题.
B 组
第 2 题.
证明:
= (1, -1),
= (1, -1)
∴AB//CD.
4. 已知点 A(0, 1), B(1, 0), C(1, 2), D(2, 1), 试判断 AB 与 CD 的位置关系, 并给出证明.
解:
如图,
x
y
o
·
·
A
B
C
D
观察估计,
AB//CD.
练习: (课本100页)
解:
如图,
设P(x, y),
方向相反,
即 (x-2, y-3)= (4-x, -3-y),
得
解得
∴点P的坐标为P(8, -15).
7. 已知点A(2, 3), B(4, -3), 点P在线段AB的延长线上, 且 求点P的坐标.
A
P
B
7. 已知点 O(0, 0), A(1, 2), B(-1, 3), 且
求点 A?、B? 及向量 的坐标.
解:
由 得
设A?(x1, y1), B?(x2, y2),
(x1, y1) = 2(1, 2),
得 x1=2, y1=4,
? A?(2, 4).
由 得
(x2, y2) = 3(-1, 3),
得 x2= -3, y2=9,
? B?(-3, 9).
(-3-2, 9-4)
=(-5, 5).
∴各坐标为A?(2, 4), B?(-3, 9), =(-5, 5).
习题 2.3
A 组
2. 判断下列各点的位置关系, 并给出证明:
(1) A(1, 2), B(-3, -4), C(2, 3.5);
(2) P(-1, 2), Q(0.5, 0), R(5, -6);
(3) E(9, 1), F(1, -3), G(8, 0.5).
(1)
=(-4, -6),
=(1, 1.5),
又-4?1.5 - (-6) ?1=0,
∴A、B、C三点共线.
x
y
o
A
B
C
·
·
·
如图,
A、B、C 共线.
证明:
∴ 与 共线,
而 、 共点A,
B 组
2. 判断下列各点的位置关系, 并给出证明:
(1) A(1, 2), B(-3, -4), C(2, 3.5);
(2) P(-1, 2), Q(0.5, 0), R(5, -6);
(3) E(9, 1), F(1, -3), G(8, 0.5).
(2)
=(1.5, -2),
=(4.5, -6),
又1.5 ?(-6)-(-2)?4.5=0,
∴P、Q、R三点共线.
x
y
o
P
R
Q
·
·
·
如图,
P、Q、R 共线.
证明:
∴ 与 共线,
而 、 共点Q,
B 组
2. 判断下列各点的位置关系, 并给出证明:
(1) A(1, 2), B(-3, -4), C(2, 3.5);
(2) P(-1, 2), Q(0.5, 0), R(5, -6);
(3) E(9, 1), F(1, -3), G(8, 0.5).
(3)
=(-8, -4),
=(7, 3.5),
又-8?3.5 - (-4) ?7=0,
∴E、F、G三点共线.
x
y
o
E
G
F
·
·
·
如图,
E、F、G 共线.
证明:
∴ 与 共线,
而 、 共点F,
B 组
复习
提高
与
与
复
习
提高
返回目录
知识要点
1. 向量基本定理
平面内任一向量 a, 都可用平面内不共线的两向量 e1、e2 的数乘的和表示, 即
e1、e2 称为一组基底.
a = l1e1+l2e2 (l1, l2?R).
2. 两向量的夹角
起点重合时的两向量的夹角,
范围是 [0?, 180?].
知识要点
3. 向量的坐标表示
在平面直角坐标系中, 分别取 x 轴、y 轴方向的单位向量 i、j 作为一组基底, 对坐标平面内的任一向量 a 作正交分解,
(x, y) 叫做向量 a 的坐标, 记作
a = xi+yj
a = (x, y).
若 a=(x1, y1), b=(x2, y2), 当且仅当
时 a=b.
知识要点
4. 向量的坐标运算
A(x1, y1), B(x2, y2)
(1)
(2)
(3)
知识要点
5. 向量共线的坐标表示
设
两向量共线, 其 x、y 坐标交叉相乘相等.
若 x1y2-x2y1=0, 则 与 共线.
知识要点
6. 线段的分点坐标
设 P(x, y), P1(x1, y1), P2(x2, y2),
(1) 若 P 是 P1P2 的中点, 则
(2) 若 则
例题选讲
解:
法一:
设点 B 的坐标为 (x, y),
由已知得点 A 的坐标为(-2, 3),
= (3, 1),
得 x+2=3, y-3=1,
解得 x=1, y=4,
∴点 B 的坐标为 (1, 4).
法二:
= (-2, 3) + (3, 1)
= (1, 4),
∴点 B 的坐标为 (1, 4).
例 1. 已知 O 为坐标原点, = (-2, 3), = (3, 1), 求点 B 的坐标.
例2. 若向量 a=(1, 2), b=(1, -1), 则 2a+b 与 a-b 的夹角等于 ( )
(A) (B) (C) (D)
解:
2(1, 2)+(1, -1)
=(2+1, 4-1)
=(3, 3).
(1, 2)-(1, -1)
=(1-1, 2+1)
=(0, 3).
x
y
O
3
3
45?
C
例3. 已知向量 a=(1, 2), b=(1, 0), c=(3, 4), l 为实数, (a+lb)//c, 则 |l(a+b)-c| 等于 .
解:
=(1+l, 2).
由 (a+lb)//c 得
4(1+l)-2?3=0,
解得
于是
=(-2, -3).
x
y
O
-2
-3
则
例4. 已知向量 a, b 不共线, c=ka+b (k?R), d=a-b, 如果 c//d, 那么 ( )
(A) k=1 且 c 与 d 同向 (B) k=1 且 c 与 d 反向
(C) k= -1 且 c 与 d 同向 (D) k= -1 且 c 与 d 反向
得 k=l,
1= -l.
? k= -1.
则
∴ 与 反向.
解:
D
排除 A, B.
解:
O
A
B
P
例5. 如图, 不共线, (t?R),
用 表示
问题: 上例中, 向量 的系数有什么关系?
结论: 如果A、B、C三点共线, O是平面内任一点, 则 (l, m?R), 且l+m =1.
返回目录
(共 9 题)
练
习
题
练习(补充)
1. 设向量 a 是 b 的相反向量, 且 b=(2, 1), 则 a 的坐标为 .
2. 设向量 a=(1, 2), b=(2, 3), 若向量 la+b 与向量 c=(-4, -7) 平行, 则 l= .
3. 设向量 a=(1, 3), b=(4, 2), c=(x, 1), 若向量a-b 与 2c 共线, 则 |c|= . a 与 c 的夹角等于 .
4. 已知两个非零向量 a, b 满足 |a+b|=|a-b|, 则下面结论正确的是 ( )
(A) a//b (B) a⊥b (C) |a|=|b| (D) a+b=a-b
5. 已知向量 a⊥b, |a|=1, |b|=2, 则 |2a-b| 等于 ( )
(A) 2 (B) (C) (D) 4
6. 若非零向量 a, b 满足 |a|=|b|, (2a+b)⊥b, 则a 与 b 的夹角为 ( )
(A) 30? (B) 60? (C) 120? (D) 150?
7. 已知 O、A、B 是平面上的三个点, 直线 AB上有一点 C, 满足
则 等于 ( )
(A) (B) (C) (D)
8. 在平行四边形 ABCD 中, AC 与 BD 交于点 O, E 是线段 OD 的中点, AE 的延长线与 CD 交于点 F, 若 则 等于 ( )
(A) (B) (C) (D)
习题2.3 B组 第 4 题
1. 设向量 a 是 b 的相反向量, 且 b=(2, 1), 则 a 的坐标为 .
解:
= -(2, 1)
= (-2, -1).
(-2, -1)
2. 设向量 a=(1, 2), b=(2, 3), 若向量 la+b 与向量 c=(-4, -7) 平行, 则 l= .
解:
与 平行得
-7(l+2)= -4(2l+3),
解得 l=2.
2
3. 设向量 a=(1, 3), b=(4, 2), c=(x, 1), 若向量a-b 与 2c 共线, 则 |c|= . a 与 c 的夹角等于 .
解:
(-3, 1),
由 a-b 与 2c 共线得
-6=2x,
得 x= -3.
x
y
O
2
-3
4
1
3
1
2
如图, ∠1=∠2.
∴ 与 的夹角为90?.
90?
4. 已知两个非零向量 a, b 满足 |a+b|=|a-b|, 则下面结论正确的是 ( )
(A) a//b (B) a⊥b (C) |a|=|b| (D) a+b=a-b
分析:
与 是一平形四边形的
两对角线长.
如图,
对角线相等的平行
四边形是矩形.
B
5. 已知向量 a⊥b, |a|=1, |b|=2, 则 |2a-b| 等于 ( )
(A) 2 (B) (C) (D) 4
解:
如图,
等腰直角三角形.
和 构成
C
6. 若非零向量 a, b 满足 |a|=|b|, (2a+b)⊥b, 则a 与 b 的夹角为 ( )
(A) 30? (B) 60? (C) 120? (D) 150?
解:
如图, 试画一个 2a+b.
A
B
C
要使
即∠ACB 是直角.
∵|a|=|b|,
在直角△ABC中, 一条直角边是斜边的一半.
∴∠ABC=60?.
则 与 的夹角为
120?.
C
7. 已知 O、A、B 是平面上的三个点, 直线 AB上有一点 C, 满足 则 等于 ( )
(A) (B)
(C) (D)
解:
由 得 (如图)
A
B
C
A 为 BC 的中点.
O
解得
A
8. 在平行四边形 ABCD 中, AC 与 BD 交于点 O, E 是线段 OD 的中点, AE 的延长线与 CD 交于点 F,若 则 等于 ( )
(A) (B)
(C) (D)
A
B
C
D
O
E
F
解:
G
作OG//AF交CD于G,
则在△DOG中, DF=FG,
在△CAF中, CG=GF.
得CG=GF=FD.
B
4. 如图, 设 Ox、Oy 是平面内相交成 60?角的两条数轴, e1、e2分别是与 x 轴、y 轴正方向同向的单位向量, 若向量 = xe1+ye2, 则把有序数对 (x, y) 叫做向量 在坐标系 xOy 中的坐标. 假设 =3e1+2e2,
(1) 计算 的大小;
(2) 由平面向量基本定理, 本题中向量坐标的规定是否合理?
B
C
解:
(1)
如图, 作PC⊥x 轴于 C,
则 |BC| =2cos60?=1,
|PC| =2sin60?
由题设得 |OB|=3, |BP|=2,
x
y
O
a
P
e1
e2
习题2.3 B组
4. 如图, 设 Ox、Oy 是平面内相交成 60?角的两条数轴, e1、e2分别是与 x 轴、y 轴正方向同向的单位向量, 若向量 = xe1+ye2, 则把有序数对 (x, y) 叫做向量 在坐标系 xOy 中的坐标. 假设 =3e1+2e2,
(1) 计算 的大小;
(2) 由平面向量基本定理, 本题中向量坐标的规定是否合理?
B
C
解:
(2)
x
y
O
a
P
e1
e2
本题向量坐标的规定
是合理的.
按题中规定, 一定存在
唯一数对 x, y, 使
习题2.3 B组
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
平面向量的基本定理
及
2.3
坐标表示
2.3.1 平面向量基本定理
复习与提高
2.3.2 平面向量坐标表示
2.3.3 平面向量坐标运算
2.3.4 平面向量共线的坐标表示
2.3.1
平面向量基本定理
返回目录
学习要点
1. 什么叫基底? 基底有什么特性? 基底的作用是什么?
2. 平面内任一向量如何用基底表示?
3. 向量的夹角是指什么样的角? 它在什么范围内?
操作题: 任画不共线的两向量 e1、e2 和另一向量 a, 作图: 用 e1、e2 的向量数乘之和表示 a .
(1)
O
A
(2)
B
(3)
C
(4)
使点E在OB上,
(5)
E
取一个实数l1,
平面向量基本定理: 如果 e1、e2 是同一平面内的两个不共线向量, 那么对于这一平面内的任一向量 a, 有且只有一对实数 l1、l2, 使
a = l1e1+l2e2.
即: 平面内任一向量 a, 可用平面内不共线的两向量 e1、e2表示. e1、e2叫做表示平面内所有向量的一组基底.
(一)基本定理
例1. 已知向量 e1、e2, 求作向量 -2.5e1+3e2.
A
B
C
e1
e2
作法:
(1)
(2)
练习: (补充)
1. 如图, 已知向量 e1、e2, 求作下列向量:
(1) 3e1+2e2;
(2) 4e1-e2;
(3)
e1
e2
习题 2.3
B 组
第 3 题.
1. 如图, 已知向量 e1、e2, 求作下列向量:
(1) 3e1+2e2;
(2) 4e1-e2;
(3)
e1
e2
(1)
(2)
(3)
练习: (补充)
3. 设 e1、e2 是平面内一组基底, 证明: 当
l1e1+l2e2=0
时, 恒有
l1=l2=0.
证明:
假设 l1≠0, l2≠0,
则 l1e1+l2e2=0 可变为
于是得 共线,
而 是一组基底, 不能共线.
∴假设不成立, 则 l1=l2=0成立.
习题 2.3
B 组
(二) 向量的夹角
设两非零向量
则∠AOB=q 叫向量 与 的夹角.
0?≤q≤180?
如果 与 的夹角是90?时, 就说 与 垂直记作
a
b
a
b
O
A
B
q
问题1: 如果向量 a 与 b 同向时, 它们的夹角等于
a 与 b 反向时
多少?
呢?
0?,
, 它们的夹角等于180?.
问题2: 下面标注的角中, 哪些角等于向量 a 与 b的夹角?
①
②
③
④
⑤
a
b
a
b
a
b
a
b
a
b
b
a
b
b
b
标注的角等于向量 a 与 b 的夹角的有
①
④
②③⑤中, 标注的角与向量 a 与 b 的夹角互补.
问题3. 在等边三角形ABC中, D是BC的中点.
(1) 向量 与 的夹角是多少?
(2) 向量 与 的夹角是多少?
(3) 向量 与 的夹角是多少?
(4) 向量 与 的夹角是多少?
A
B
C
D
60?
30?
90?
120?
练习(补充)
1. 设非零向量 a, b, c, 满足 |a|=|b|=|c|, a+b=c,则 a 与 b 的夹角等于 ( )
(A) 150? (B) 120? (C) 60? (D) 30?
2. 平面向量 a 与 b 的夹角为 60?, |a|=2, |b|=1,则 |a+2b| 的模等于 ( )
(A) (B) (C) 4 (D) 12
1. 设非零向量 a, b, c, 满足 |a|=|b|=|c|, a+b=c,则 a 与 b 的夹角等于 ( )
(A) 150? (B) 120? (C) 60? (D) 30?
解:
由三角形法则作 a+b=c,
由 |a|=|b|=|c| 得三角形是等边三角形.
得 a 与 b 的夹角应是
B
120?.
2. 平面向量 a 与 b 的夹角为 60?, |a|=2, |b|=1,则 |a+2b| 的模等于 ( )
(A) (B) (C) 4 (D) 12
解:
画出 a 与 b 的夹角为 60?, |a|=2, |b|=1.
60?
再由平行四边形法则画 a+2b,
A
B
C
D
在△ABC 中可求得
B
【课时小结】
1. 向量基本定理
平面内任一向量 a, 都可用平面内不共线的两向量 e1、e2 的数乘的和表示, 即
e1、e2 称为一组基底.
a = l1e1+l2e2 (l1, l2?R).
【课时小结】
2. 两向量的夹角
0?≤q≤180?.
a
b
a
b
O
A
B
q
起点重合时的两向量的夹角,
范围是 [0?, 180?].
练习: (补充)
1. 在△ABC中, D是AB上的点, 且AD:DB=1:2, 设 用 表示
O
A
B
C
2. 如图, 是单位向量, 且
与 的夹角为30?,
试用 表示
3. 在△ABC中, 作
AE、EF分别是△ABC的什么线?
4. 已知单位向量 a⊥b, 向量 c 满足 a-c⊥b-c, 则 |c| 的最大值等于多少?
1. 在△ABC中, D是AB上的点, 且AD:DB=1:2, 设 用 表示
A
C
B
D
解:
由 AD:DB=1:2 得
如图,
O
A
B
C
2. 如图, 是单位向量, 且 与 的夹角为30?, 试用 表示
解:
作CD⊥OB (延长线) 于D,
D
在Rt△CDO中, 由已知得
OC=2, ∠COD=30?,
∴CD=1,
则
3. 在△ABC中, 作
AE、EF分别是△ABC的什么线?
A
C
B
E
M
作法:
① 取AB的中点M,
F
则ME为△ABC的中位线,
作ME//AC, 交BC于E,
② 作EF//BA, 交AC于F,
得
∴ 为所求.
则
答: AE是△ABC的中线, EF是一条中位线.
4. 已知单位向量 a⊥b, 向量 c 满足 a-c⊥b-c, 则 |c| 的最大值等于多少?
解:
如图, 单位向量 a⊥b,
要作 a-c, b-c,
向量减法, 起点重合.
作出 a-c, b-c.
∵a⊥b, a-c⊥b-c,
A
B
∴向量 c 的终点 C 在以 AB 为直径的圆上.
C
则 |c| 最大时是这个圆的直径.
∵a, b 是单位向量,
则
2.3.2
平面向量的正交分解
2.3.3
平面向量的坐标运算
及坐标表示
返回目录
学习要点
1. 什么叫正交分解?
2. 直角坐标平面内的向量是以什么作为一组基底的?
3. 向量的坐标是怎样确定的? 两向量相等时, 坐标有什么关系?
4. 向量的坐标运算法则是怎样的?
2.3.2 平面向量的正交分解及坐标表示
为了借助于坐标平面研究向量, 需要把一个向量分解成两个互相垂直的向量.
把一个向量分解为两个互相垂直的向量, 叫做把向量正交分解.
(一) 向量的正交分解
在物理学中, 我们学过力的分解与合成.
同样, 我们也可以对平面向量进行分解.
如图:
将向量 分解成水平和竖直的两个向量.
O
A
B
C
(二) 向量的坐标表示
在平面直角坐标系中, 分别取 x 轴、y 轴方向的单位向量 i、j 作为一组基底.
根据向量基本定理, 坐标平面内的任一向量 a 都可用向量 i、j 表示.
x
y
o
i
j
a
b
4i
2j
3i
-6j
的坐标表示为:
图中向量
如图:
定义: 在直角坐标系内, 取 x 轴、 y 轴方向的一组单位向量 i、j 为基底, 任一向量 a 唯一存在一对实数 x、y, 使得
a = xi+yj
我们把 (x, y) 叫做向量 a 的坐标, 记作
a = (x, y),
这种表示叫做向量的坐标表示.
显然, i = (1, 0), j = (0, 1),
若 a=(x1, y1), b=(x2, y2), 当且仅当
时 a=b.
例2. 如图, 分别用基底 i、j 表示向量 a、b、c, 并写出它们的坐标.
x
y
o
i
j
解:
= (2, 3).
= (5, 0).
= (-5, 1).
练习: (补充)
1. 如图, 分别用基底 i、j 表示向量 a、b、c、d、e、f, 并写出它们的坐标.
i
1
2
3
4
-1
-2
-3
-4
-5
1
2
3
4
5
-1
-2
-3
-4
x
y
o
j
A
A1
A2
解:
= (2, 3).
= (2, 3).
= (-2, 3).
= (-2, -3).
= (4, -2).
= (2, -3).
问题1: 设向量 a = ( x1, y1 ), b = ( x2, y2 ), 则a+b = ( x1+x2, y1+y2 ) 是否成立? la=(lx1, ly1) 是否成立? 为什么?
2.3.3 平面向量的坐标运算
答: 上述结论成立.
结论:
两个向量和 ( 差 ) 的坐标分别等于这两个向量相应坐标的和 ( 差 ).
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
例4. 已知 a=(2, 1), b=(-3, 4), 求 a+b, a-b, 3a+4b 的坐标.
解:
= (-1, 5);
= (5, -3);
= (6, 3) + (-12, 16)
= (-6, 19).
2. 已知 a=(3, 2), b=(0, -1), 求 -2a+4b, 4a+3b 的坐标.
解:
= (-6, -4) + (0, -4)
= (-6, -8);
= (12, 8) + (0, -3)
= (12, 5).
练习: (课本100页)
问题:
B 的坐标就是 (5, 2) 吗? 如果起点A的坐标是 (-2, -3), 画图看看, 终点B的坐标应该是多少?
x
y
o
B
A
B
A
A
B
A
B
A
B
(3, -1)
(5, 2)
终点 B 的坐标就不是(5, 2).
如果起点 A 不在原点,
如果起点A(-2, -3),
终点B(3, -1).
如果起点在原点,
则终点为
-2
-3
B(5, 2).
5
2
例3. 已知 O 为原点, 点 A、B 的坐标为A(x1, y1), B(x2, y2),
解:
由 A(x1, y1), B(x2, y2) 得
结论: 一个向量的坐标等于这个向量的终点坐标减去起点坐标.
x
o
y
A
B
C
D
-2
3
1
4
例5. 如图, 已知□ABCD的三个顶点A、B、C 的坐标分别是 (-2, 1) 、 (-1, 3) 、 (3, 4), 试求顶点 D的坐标.
解:
在□ABCD中,
(-1+2,
3-1)
=(1, 2),
设点 D(x, y),
则
(3-x,
4-y),
由 得
(1, 2) = (3-x, 4-y),
得
解得
∴顶点 D 的坐标是(2, 2).
x
o
y
A
B
C
D
-2
3
1
4
例5. 如图, 已知□ABCD的三个顶点A、B、C 的坐标分别是 (-2, 1) 、 (-1, 3) 、 (3, 4), 试求顶点 D的坐标.
解:
法二,
+(4, 1)
= (3, -1),
= (-1, -2)
设点 D(x, y),
由 的和向量表示:
而 的坐标等于终点坐标减起点坐标,
即(3, -1) = (x+1, y-3),
得
解得
∴顶点 D 的坐标是(2, 2).
练习: (课本100页)
第 1、3 题.
1. 已知向量 a, b 的坐标, 求 a+b, a-b 的坐标.
(1) a=(-2, 4), b=(5, 2); (2) a=(4, 3), b=(-3, 8);
(3) a=(2, 3), b=(-2, -3); (4) a=(3, 0), b=(0, 4).
解: (1)
(2)
(3)
(4)
= (3, 6);
= (-7, 2).
= (1, 11);
= (7, -5).
= (0, 0);
= (4, 6).
= (3, 4);
= (3, -4).
练习: (课本100页)
3. 已知A、B两点的坐标, 求 的坐标.
(1) A(3, 5), B(6, 9); (2) A(-3, 4), B(6, 3);
(3) A(0, 3), B(0. 5); (4) A(3. 0), B(8, 0).
解: (1)
= (3, 4);
= (-3, -4).
= (9, -1);
= (-9, 1).
= (0, 2);
= (0, -2).
= (5, 0);
= (-5, 0).
(2)
(3)
(4)
【课时小结】
1. 向量的正交分解
把一个向量分解为两个互相垂直的向量, 叫做把向量正交分解.
O
A
B
C
x
y
o
a
x
y
a=x+y.
【课时小结】
2. 向量的坐标表示
在平面直角坐标系中, 分别取 x 轴、y 轴方向的单位向量 i、j 作为一组基底, 对坐标平面内的任一向量 a 作正交分解,
如图, 正交分解向量 a
(x, y) 叫做向量 a 的坐标, 记作
a = xi+yj
x
y
O
a = (x, y).
向量 a 的坐标表示
【课时小结】
3. 向量的坐标运算
A(x1, y1), B(x2, y2)
(1)
(2)
(3)
若 a=(x1, y1), b=(x2, y2), 当且仅当
时 a=b.
习题2.3
第 1、2、3、4 题.
A 组
第 1 题.
B 组
解:
设终点B的坐标为(x, y),
(1)
=(-2, 1),
? x= -2, y=1,
∴终点 B 的坐标为(-2, 1);
(2)
=(1, 3),
得 x+1=1, y-5=3,
∴终点 B 的坐标为(0, 8);
解得 x=0, y=8,
(3)
=(-2, -5)
得 x-3= -2, y-7= -5,
∴终点 B 的坐标为(1, 2).
解得 x=1, y=2,
1. 已知表示向量 a 的有向线段始点 A 的坐标, 求它的终点 B 的坐标:
(1) a=(-2, 1), A(0, 0); (2) a=(1, 3), A(-1, 5);
(3) a=(-2, -5), A(3, 7).
习题2.3
A 组
解:
∵三个力都作用在坐标原点,
∴F1+F2+F3= (3, 4) + (2, -5) + (3, 1)
= (8, 0).
2. 已知作用在坐标原点的三个力F1=(3, 4), F2=(2, -5), F3=(3, 1), 求作用在原点的合力F1+F2+F3的坐标.
解:
设点 D 的坐标为(x, y),
= (2, 7),
= ( x+1, y+2 ),
∴有 x+1=2, y+2=7,
解得 x=1, y=5,
∴点 D 的坐标为(1, 5).
3. 已知□ABCD的顶点 A(-1, -2), B(3, -1), C(5, 6), 求顶点 D 的坐标.
4. 已知点A(1, 1), B(-1, 5)及
求点 C、D、E 的坐标.
解:
(-1-1, 5-1)
=(-2, 4),
设 C(x1, y1) 、D(x2, y2) 、E(x3, y3),
① 由 得
(x1-1, y1-1)= (-2, 4),
得
解得 x1=0, y1=3,
?C(0, 3).
② 由 得
(x2-1, y2-1)=2(-2, 4),
得
解得 x2= -3, y2=9,
?D(-3, 9).
③ 由 得
(x3-1, y3-1)= (-2, 4),
得
解得 x3=2, y3= -1,
?E(2, -1).
解:
=(3, 3),
当t =1时,
=(1, 2) + (3, 3)
=(4, 5),
当t= -2时,
=(1, 2) -2(3, 3)
=(-5, -4),
当t =2时,
=(1, 2)+2(3, 3)
=(7, 8),
1. 已知点O(0, 0), A(1, 2), B(4, 5),
当 t=1, -2, 2时, 分别求点 P 的坐标.
由已知得
得P点的坐标为(4, 5).
得P点的坐标为(-5, -4).
得P点的坐标为
得P点的坐标为(7, 8).
B 组
2.3.4
平面向量共线
的坐标表示
返回目录
学习要点
1. 用坐标表示向量时, 两向量共线的条件是什么?
2. 怎样用向量的坐标求线段分点的坐标?
问题1. 两非零向量 共线的条件是什么? 试推导一下, 它们的坐标存在什么关系?
答: 当且仅当存在实数l, 使
则 与 共线.
设
则 (x1, y1) = l(x2, y2),
得
消去l得 x1y2-x2y1=0.
或
x1y2=x2y1
结论: 两非零向量共线, 其 x、y 坐标交叉相乘相等.
坐标关系:
(一) 向量共线的坐标表示
例6. 已知 a=(4, 2), b=(6, y), 且a∥b, 求 y.
解:
∴4y-2?6=0,
解得 y=3.
例7. 已知A(-1, -1), B(1, 3), C(2, 5), 试判断A, B, C 三点之间的位置关系.
解:
= (2, 4),
= (1, 2),
又 2?2 - 4?1 = 0.
∴A, B, C 三点在一条直线上.
分析:
则考虑共点的两向量是否共线.
∴ 与 共线,
而 与 共点B,
x
y
o
A
B
C
·
·
·
-1
-1
1
3
2
5
如图,
A、B、C 三点共线,
观察估计,
练习:
A 组
习题 2.3
第 5、6 题.
解:
解得 x = -4,
5. x 为何值时, a=(2, 3) 与 b=(x, -6) 共线?
若 共线,
则2?(-6)-3x=0,
即 x= -4 时 与 共线.
A 组
习题 2.3
解:
而 4(-8) - 4(-8) = 0,
6. 已知A(-2, -3), B(2, 1), C(1, 4), D(-7, -4), 试问 与 是否共线?
由题设得
(二) 线段的分点
例8. 设点 P 是线段P1P2上的一点, P1、P2的坐标分别是 (x1, y1), (x2, y2).
(1) 当点 P 是线段 P1P2 的中点时, 求点 P 的坐标;
(2) 当点 P 是线段 P1P2 的一个三等分点时, 求点 P 的坐标.
解:
(1)
∵P 是线段 P1P2 的中点
设 P 点的坐标为 P(x, y),
则 (x-x1, y-y1) = (x2-x, y2-y),
即
得线段中点的坐标公式:
(二) 线段的分点
例8. 设点 P 是线段P1P2上的一点, P1、P2的坐标分别是 (x1, y1), (x2, y2).
(1) 当点 P 是线段 P1P2 的中点时, 求点 P 的坐标;
(2) 当点 P 是线段 P1P2 的一个三等分点时, 求点 P 的坐标.
解:
(2)
同理, 设 P(x, y),
若
P1
P2
P
则 (x-x1, y-y1) = (x2-x, y2-y),
若
P1
P2
P
练习: (课本100页)
第 5、6 题.
练习: (补充)
设P1、P2的坐标分别是(x1, y1), (x2, y2). 点 P 是直线P1P2上的一点, 若 求点 P 的坐标.
5. 求线段 AB 的中点坐标:
(1) A(2, 1), B(4, 3);
(2) A(-1, 2), B(3, 6);
(3) A(5, -4), B(3, -6).
解:
(1)
=3,
=2,
∴AB 中点的坐标是(3, 2).
(2)
同(1)得x=1,
y=4,
∴AB 中点的坐标是(1, 4).
(3)
x=4,
y= -5,
∴AB 中点的坐标是(4, -5).
6. 已知向量 =(2, 3), =(6, -3), 点 P 是线段 AB 的三等分点, 求点 P 的坐标.
解:
由 得
点A(2, 3), B(6, -3).
设两个三等分点分别为(x1, y1), (x2, y2),
则
=1,
= -1,
∴两个三等分点分别为( 1), ( -1).
练习: (补充)
设P1、P2的坐标分别是(x1, y1), (x2, y2). 点 P 是直线P1P2上的一点, 若 求点 P 的坐标.
解:
设 P 点的坐标为 P(x, y),
则 (x-x1, y-y1) = l(x2-x, y2-y),
得
结论:
P1(x1, y1), P2(x2, y2), P(x, y) 分P1P2为
则
分点坐标
公式
【课时小结】
1. 向量共线的坐标表示
设
两向量共线, 其 x、y 坐标交叉相乘相等.
若 x1y2-x2y1=0, 则 与 共线.
【课时小结】
2. 线段的分点坐标
设 P(x, y), P1(x1, y1), P2(x2, y2),
(1) 若 P 是 P1P2 的中点, 则
(2) 若 则
A 组
习题 2.3
练习: (课本100页)
第 4、7 题.
第 7 题.
B 组
第 2 题.
证明:
= (1, -1),
= (1, -1)
∴AB//CD.
4. 已知点 A(0, 1), B(1, 0), C(1, 2), D(2, 1), 试判断 AB 与 CD 的位置关系, 并给出证明.
解:
如图,
x
y
o
·
·
A
B
C
D
观察估计,
AB//CD.
练习: (课本100页)
解:
如图,
设P(x, y),
方向相反,
即 (x-2, y-3)= (4-x, -3-y),
得
解得
∴点P的坐标为P(8, -15).
7. 已知点A(2, 3), B(4, -3), 点P在线段AB的延长线上, 且 求点P的坐标.
A
P
B
7. 已知点 O(0, 0), A(1, 2), B(-1, 3), 且
求点 A?、B? 及向量 的坐标.
解:
由 得
设A?(x1, y1), B?(x2, y2),
(x1, y1) = 2(1, 2),
得 x1=2, y1=4,
? A?(2, 4).
由 得
(x2, y2) = 3(-1, 3),
得 x2= -3, y2=9,
? B?(-3, 9).
(-3-2, 9-4)
=(-5, 5).
∴各坐标为A?(2, 4), B?(-3, 9), =(-5, 5).
习题 2.3
A 组
2. 判断下列各点的位置关系, 并给出证明:
(1) A(1, 2), B(-3, -4), C(2, 3.5);
(2) P(-1, 2), Q(0.5, 0), R(5, -6);
(3) E(9, 1), F(1, -3), G(8, 0.5).
(1)
=(-4, -6),
=(1, 1.5),
又-4?1.5 - (-6) ?1=0,
∴A、B、C三点共线.
x
y
o
A
B
C
·
·
·
如图,
A、B、C 共线.
证明:
∴ 与 共线,
而 、 共点A,
B 组
2. 判断下列各点的位置关系, 并给出证明:
(1) A(1, 2), B(-3, -4), C(2, 3.5);
(2) P(-1, 2), Q(0.5, 0), R(5, -6);
(3) E(9, 1), F(1, -3), G(8, 0.5).
(2)
=(1.5, -2),
=(4.5, -6),
又1.5 ?(-6)-(-2)?4.5=0,
∴P、Q、R三点共线.
x
y
o
P
R
Q
·
·
·
如图,
P、Q、R 共线.
证明:
∴ 与 共线,
而 、 共点Q,
B 组
2. 判断下列各点的位置关系, 并给出证明:
(1) A(1, 2), B(-3, -4), C(2, 3.5);
(2) P(-1, 2), Q(0.5, 0), R(5, -6);
(3) E(9, 1), F(1, -3), G(8, 0.5).
(3)
=(-8, -4),
=(7, 3.5),
又-8?3.5 - (-4) ?7=0,
∴E、F、G三点共线.
x
y
o
E
G
F
·
·
·
如图,
E、F、G 共线.
证明:
∴ 与 共线,
而 、 共点F,
B 组
复习
提高
与
与
复
习
提高
返回目录
知识要点
1. 向量基本定理
平面内任一向量 a, 都可用平面内不共线的两向量 e1、e2 的数乘的和表示, 即
e1、e2 称为一组基底.
a = l1e1+l2e2 (l1, l2?R).
2. 两向量的夹角
起点重合时的两向量的夹角,
范围是 [0?, 180?].
知识要点
3. 向量的坐标表示
在平面直角坐标系中, 分别取 x 轴、y 轴方向的单位向量 i、j 作为一组基底, 对坐标平面内的任一向量 a 作正交分解,
(x, y) 叫做向量 a 的坐标, 记作
a = xi+yj
a = (x, y).
若 a=(x1, y1), b=(x2, y2), 当且仅当
时 a=b.
知识要点
4. 向量的坐标运算
A(x1, y1), B(x2, y2)
(1)
(2)
(3)
知识要点
5. 向量共线的坐标表示
设
两向量共线, 其 x、y 坐标交叉相乘相等.
若 x1y2-x2y1=0, 则 与 共线.
知识要点
6. 线段的分点坐标
设 P(x, y), P1(x1, y1), P2(x2, y2),
(1) 若 P 是 P1P2 的中点, 则
(2) 若 则
例题选讲
解:
法一:
设点 B 的坐标为 (x, y),
由已知得点 A 的坐标为(-2, 3),
= (3, 1),
得 x+2=3, y-3=1,
解得 x=1, y=4,
∴点 B 的坐标为 (1, 4).
法二:
= (-2, 3) + (3, 1)
= (1, 4),
∴点 B 的坐标为 (1, 4).
例 1. 已知 O 为坐标原点, = (-2, 3), = (3, 1), 求点 B 的坐标.
例2. 若向量 a=(1, 2), b=(1, -1), 则 2a+b 与 a-b 的夹角等于 ( )
(A) (B) (C) (D)
解:
2(1, 2)+(1, -1)
=(2+1, 4-1)
=(3, 3).
(1, 2)-(1, -1)
=(1-1, 2+1)
=(0, 3).
x
y
O
3
3
45?
C
例3. 已知向量 a=(1, 2), b=(1, 0), c=(3, 4), l 为实数, (a+lb)//c, 则 |l(a+b)-c| 等于 .
解:
=(1+l, 2).
由 (a+lb)//c 得
4(1+l)-2?3=0,
解得
于是
=(-2, -3).
x
y
O
-2
-3
则
例4. 已知向量 a, b 不共线, c=ka+b (k?R), d=a-b, 如果 c//d, 那么 ( )
(A) k=1 且 c 与 d 同向 (B) k=1 且 c 与 d 反向
(C) k= -1 且 c 与 d 同向 (D) k= -1 且 c 与 d 反向
得 k=l,
1= -l.
? k= -1.
则
∴ 与 反向.
解:
D
排除 A, B.
解:
O
A
B
P
例5. 如图, 不共线, (t?R),
用 表示
问题: 上例中, 向量 的系数有什么关系?
结论: 如果A、B、C三点共线, O是平面内任一点, 则 (l, m?R), 且l+m =1.
返回目录
(共 9 题)
练
习
题
练习(补充)
1. 设向量 a 是 b 的相反向量, 且 b=(2, 1), 则 a 的坐标为 .
2. 设向量 a=(1, 2), b=(2, 3), 若向量 la+b 与向量 c=(-4, -7) 平行, 则 l= .
3. 设向量 a=(1, 3), b=(4, 2), c=(x, 1), 若向量a-b 与 2c 共线, 则 |c|= . a 与 c 的夹角等于 .
4. 已知两个非零向量 a, b 满足 |a+b|=|a-b|, 则下面结论正确的是 ( )
(A) a//b (B) a⊥b (C) |a|=|b| (D) a+b=a-b
5. 已知向量 a⊥b, |a|=1, |b|=2, 则 |2a-b| 等于 ( )
(A) 2 (B) (C) (D) 4
6. 若非零向量 a, b 满足 |a|=|b|, (2a+b)⊥b, 则a 与 b 的夹角为 ( )
(A) 30? (B) 60? (C) 120? (D) 150?
7. 已知 O、A、B 是平面上的三个点, 直线 AB上有一点 C, 满足
则 等于 ( )
(A) (B) (C) (D)
8. 在平行四边形 ABCD 中, AC 与 BD 交于点 O, E 是线段 OD 的中点, AE 的延长线与 CD 交于点 F, 若 则 等于 ( )
(A) (B) (C) (D)
习题2.3 B组 第 4 题
1. 设向量 a 是 b 的相反向量, 且 b=(2, 1), 则 a 的坐标为 .
解:
= -(2, 1)
= (-2, -1).
(-2, -1)
2. 设向量 a=(1, 2), b=(2, 3), 若向量 la+b 与向量 c=(-4, -7) 平行, 则 l= .
解:
与 平行得
-7(l+2)= -4(2l+3),
解得 l=2.
2
3. 设向量 a=(1, 3), b=(4, 2), c=(x, 1), 若向量a-b 与 2c 共线, 则 |c|= . a 与 c 的夹角等于 .
解:
(-3, 1),
由 a-b 与 2c 共线得
-6=2x,
得 x= -3.
x
y
O
2
-3
4
1
3
1
2
如图, ∠1=∠2.
∴ 与 的夹角为90?.
90?
4. 已知两个非零向量 a, b 满足 |a+b|=|a-b|, 则下面结论正确的是 ( )
(A) a//b (B) a⊥b (C) |a|=|b| (D) a+b=a-b
分析:
与 是一平形四边形的
两对角线长.
如图,
对角线相等的平行
四边形是矩形.
B
5. 已知向量 a⊥b, |a|=1, |b|=2, 则 |2a-b| 等于 ( )
(A) 2 (B) (C) (D) 4
解:
如图,
等腰直角三角形.
和 构成
C
6. 若非零向量 a, b 满足 |a|=|b|, (2a+b)⊥b, 则a 与 b 的夹角为 ( )
(A) 30? (B) 60? (C) 120? (D) 150?
解:
如图, 试画一个 2a+b.
A
B
C
要使
即∠ACB 是直角.
∵|a|=|b|,
在直角△ABC中, 一条直角边是斜边的一半.
∴∠ABC=60?.
则 与 的夹角为
120?.
C
7. 已知 O、A、B 是平面上的三个点, 直线 AB上有一点 C, 满足 则 等于 ( )
(A) (B)
(C) (D)
解:
由 得 (如图)
A
B
C
A 为 BC 的中点.
O
解得
A
8. 在平行四边形 ABCD 中, AC 与 BD 交于点 O, E 是线段 OD 的中点, AE 的延长线与 CD 交于点 F,若 则 等于 ( )
(A) (B)
(C) (D)
A
B
C
D
O
E
F
解:
G
作OG//AF交CD于G,
则在△DOG中, DF=FG,
在△CAF中, CG=GF.
得CG=GF=FD.
B
4. 如图, 设 Ox、Oy 是平面内相交成 60?角的两条数轴, e1、e2分别是与 x 轴、y 轴正方向同向的单位向量, 若向量 = xe1+ye2, 则把有序数对 (x, y) 叫做向量 在坐标系 xOy 中的坐标. 假设 =3e1+2e2,
(1) 计算 的大小;
(2) 由平面向量基本定理, 本题中向量坐标的规定是否合理?
B
C
解:
(1)
如图, 作PC⊥x 轴于 C,
则 |BC| =2cos60?=1,
|PC| =2sin60?
由题设得 |OB|=3, |BP|=2,
x
y
O
a
P
e1
e2
习题2.3 B组
4. 如图, 设 Ox、Oy 是平面内相交成 60?角的两条数轴, e1、e2分别是与 x 轴、y 轴正方向同向的单位向量, 若向量 = xe1+ye2, 则把有序数对 (x, y) 叫做向量 在坐标系 xOy 中的坐标. 假设 =3e1+2e2,
(1) 计算 的大小;
(2) 由平面向量基本定理, 本题中向量坐标的规定是否合理?
B
C
解:
(2)
x
y
O
a
P
e1
e2
本题向量坐标的规定
是合理的.
按题中规定, 一定存在
唯一数对 x, y, 使
习题2.3 B组
