2020-2021学年高一数学人教A版必修4第二章2.4 平面向量的数量积2课时课件(共86张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第二章2.4 平面向量的数量积2课时课件(共86张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览









文档简介
第二章
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
平面向量的数量积
2.4
2.4.1平面向量数量积的物理背景及其含义
复习与提高
2.4.2平面向量数量积的坐标表示、模、夹角
2.4.1
平面向量数量积
的
物理背景及其含义
返回目录
学习要点
1. 向量的数量积是怎样计算的? 它是一个向量还是一个数量?
2. 向量的数量积的几何意义是什么?
3. 两向量垂直的条件是什么?
4. 向量的数量积有哪些运算定律? 实数的运算定律是否有不适合向量的数量积的?
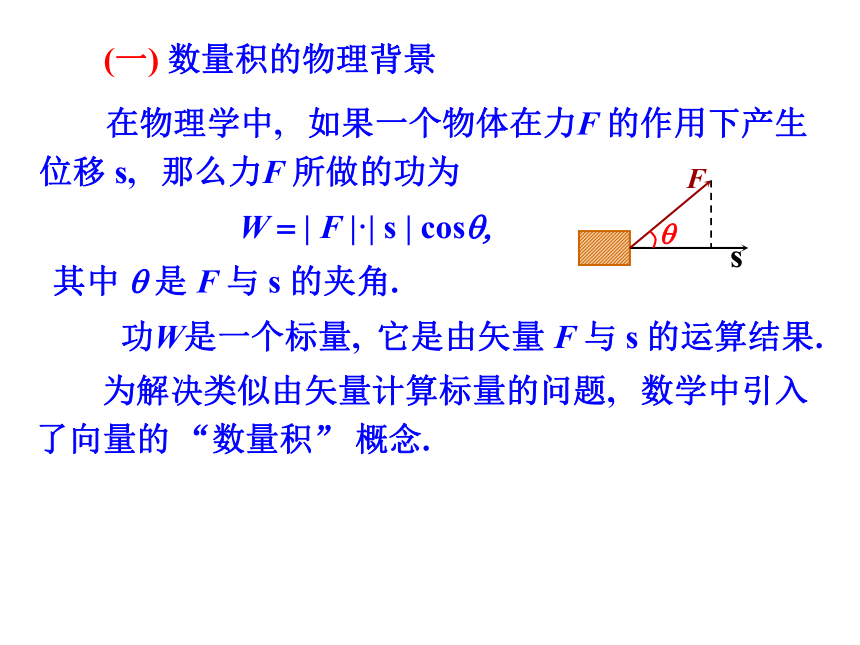
(一) 数量积的物理背景
在物理学中, 如果一个物体在力F 的作用下产生位移 s, 那么力F 所做的功为
W = | F |·| s | cosq,
其中 q 是 F 与 s 的夹角.
功W是一个标量, 它是由矢量 F 与 s 的运算结果.
为解决类似由矢量计算标量的问题, 数学中引入了向量的 “数量积” 概念.
s
F
q
(二) 向量的数量积
定义: 已知两个非零向量 a 和 b, 它们的夹角为q. 我们把数量 |a| |b|cosq 叫做 a 与 b 的数量积 (或内积), 记作 a·b, 即
a·b = |a| |b| cosq.
又规定: 零向量与任一向量的数量积为 0.
即两向量的数量积, 等于两向量的模与夹角的余弦的乘积.
练习: (课本106页)
第 1 题
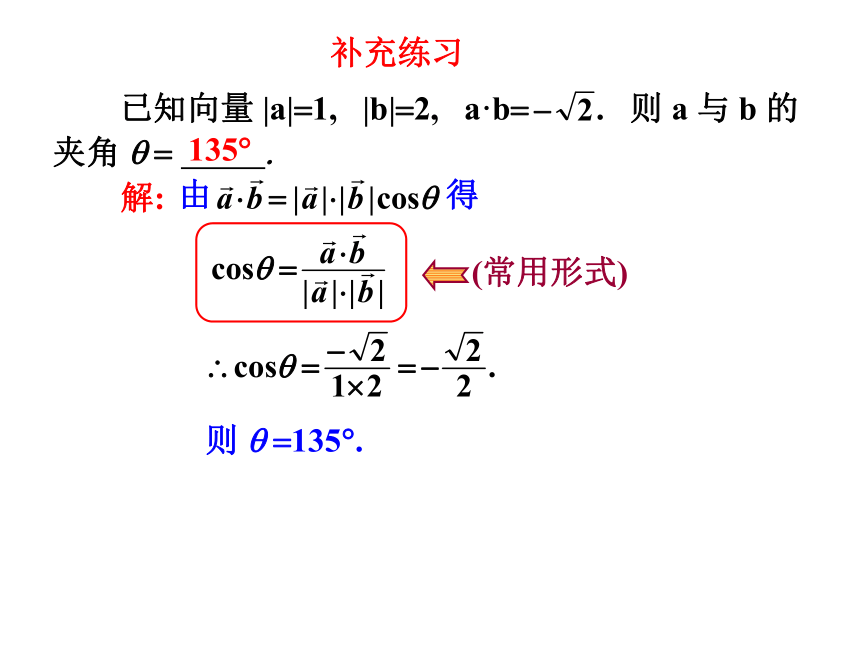
补充练习
已知向量 |a|=1, |b|=2, a·b= . 则 a 与 b 的夹角 q = .
1. 已知 |p|=8, |q|=6, p 和 q 的夹角是60?, 求 p·q.
解:
= 24.
练习: (课本106页)
补充练习
已知向量 |a|=1, |b|=2, a·b= . 则 a 与 b 的夹角 q = .
解:
由 得
则 q =135?.
(常用形式)
135?
问题1. 向量的数量积与向量的数乘有什么区别? 向量的数量积是向量还是数量?
向量的数乘是一个向量, 而向量的数量积是一个数量, 是三个数量的乘积.
q
D
表示 在 方向上的投影 (如图),
几何意义:
O
C
A
B
表示 在 方向上的投影,
即
=OC·OB
=OD·OA.
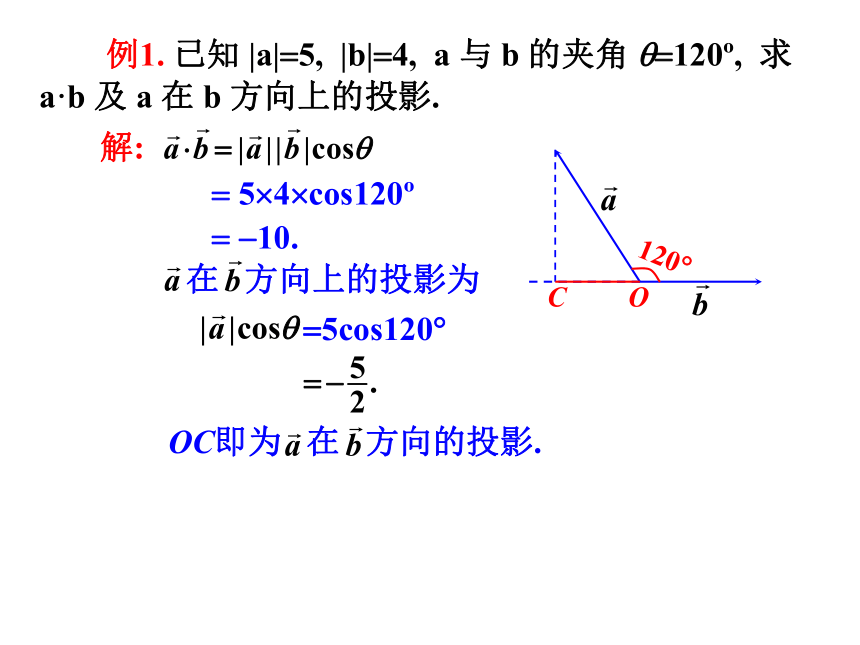
例1. 已知 |a|=5, |b|=4, a 与 b 的夹角 q=120?, 求a·b 及 a 在 b 方向上的投影.
解:
= 5?4?cos120?
= -10.
在 方向上的投影为
=5cos120?
120?
O
C
OC即为 在 方向的投影.
(1)
当q =45?时,
O
A
(2)
当q =90?时,
(3)
当q =135?时,
O
(A)
(1)
(2)
(3)
O
A
解:
各图中的投影用OA表示.
45?
●
135?
3. 已知 |a|=6, e 为单位向量, 当 a、e 之间的夹角q 分别等于 45?、90?、135? 时, 画图表示 a 在 e 方向上的投影, 并求其值.
=0.
练习: (课本106页)
问题2. 非零向量 a 与 b 的数量积 a·b 在什么情况下为正? 在什么情况下这负? 在什么情况下为零?
即两向量的夹角为锐角时, 数量积为正,
夹角为钝角时, 数量积为负,
夹角为直角时, 数量积为零.
两非零向量垂直 ??数量积为零.
解:
2. 已知△ABC中, =a, =b, 当 a·b<0 或a·b=0 时, 试判断△ABC的形状.
当 时, cosA
< 0,
则角A为钝角,
∴△ABC为钝角三角形.
当 时, cosA
= 0,
则角A为直角,
∴△ABC为直角三角形.
两非零向量垂直??数量积为0.
练习: (课本106页)
(三) 数量积的运算律
问题3. 下列等式是否成立, 为什么?
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(5) (a·b)·c=a·(b·c).
分析:
(1)
(2)
同理
即 成立.
(三) 数量积的运算律
问题3. 下列等式是否成立, 为什么?
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(5) (a·b)·c=a·(b·c).
分析:
(3)
如图,
O
A
B
C
A?
B?
D
q2
q1
q3
=|OD|·|OC|,
=|OA?|·|OC|
+|A?D|·|OC|
=|OD|·|OC|,
(三) 数量积的运算律
问题3. 下列等式是否成立, 为什么?
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(5) (a·b)·c=a·(b·c).
分析:
(4)
即 成立.
(5)
是数乘向量,
与 共线,
也是数乘向量,
但与 共线,
两向量方向不一定相同, 所以不等.
数量积运算定律
例2. 类比实数的乘法公式, 下列向量等式是否成立?
(1) (a+b)2=a2+2ab+b2;
(2) (a+b)·(a-b)=a2-b2.
答: 两等式都成立.
∴(1)式成立.
又
∴(2)式成立.
实数的乘法公式适用向量的乘法运算.
例3. 已知 |a|=6, |b|=4, a 与 b 的夹角为 60?, 求 (a+2b)·(a-3b).
解:
例4. 已知 | a |=3, | b |=4, 且 a 与 b 不共线. k 为何值时, 向量 a+kb 与 a-kb 互相垂直?
解:
两向量垂直, 其数量积为零,
= 9-16k2,
两使 9-16k2 = 0,
解得
答: 当k = 时, 向量 互相垂直.
【课时小结】
1. 向量的数量积
2. 数量积的几何意义
一个向量在另一个向量方向上的投影.
q
D
O
C
A
B
即
=OC·OB
=OD·OA.
【课时小结】
3. 向量数量积的运算定律
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(a·b)·c≠a·(b·c).
注意:
实数的乘法交换律不适应.
【课时小结】
4. 有关数量积的计算
(1) 求夹角
(2) 两非零向量垂直
(3) 两向量共线
(4) 模
习题 2.4
A 组
第 2、3、6、7、8 题.
2. 已知△ABC中, a=5, b=8, C=60?, 求
解:
(如图)
A
B
C
120?
= 120?,
= -20.
习题 2.4
A 组
3. 已知 |a|=2, |b|=5, a·b= -3, 求 |a+b|, |a-b|.
解:
解:
得 q =135?.
注意
6. 设 |a|=12, |b|=9, a·b= 求 a 与 b 的夹角q.
7. 已知 |a|=4, |b|=3, (2a-3b)·(2a+b)=61, 求 a 与b 的夹角q.
解:
由 得
64-48cosq -27=61,
解得 cosq =
得 q =120?.
8. 已知 |a|=8, |b|=10, |a+b|=16, 求 a 与 b 的夹角q (精确到1?). (可用计算器)
解:
由 得
解得cosq =
得q≈55?.
2.4.2
平
面
向
量
数
量
积
的
坐
标
表
示
模
夹
角
返回目录
学习要点
1. 用坐标表示的向量怎样计算两向量的数量积? 怎样计算两向量的夹角?
2. 用坐标表示的向量怎样计算它的模?
3. 两向量垂直时, 其坐标满足什么条件? 与两向量共线的条件有什么区别?
思考题. 已知向量 a = (x1, y1), b = (x2, y2), 用坐标怎样表示 a·b? (提示: 用 x、y 轴正方向的单位向量作基底)
分析:
设 表示 x、y 轴正方向的单位向量,
∴上式=
则
这就是向量数量积的坐标表示.
即 (x1, y1)·(x2, y2) =x1x2+y1y2.
结论:
两个向量的数量积等于它们对应坐标的乘积的和.
练习: (补充)
1. 已知向量 a、b 的坐标表示如下,求 a · b.
(1) a = (3, -1), b = (-2, -5);
(2) a = (3, -1), b = (-1, -3);
(3) a = (1, 0), b = (1, 1).
2. 设向量 a = (x, y), 求 a2 和 | a | .
解: (1)
= -6+5
= -1;
(2)
= -3+3
= 0;
= 1.
(3)
1. 已知向量 a、b 的坐标表示如下,求a · b.
(1) a = (3, -1), b = (-2, -5);
(2) a = (3, -1), b = (-1, -3);
(3) a = (1, 0), b = (1, 1).
练习: (补充)
2. 设向量 a = (x, y), 求 a2 和 | a | .
解:
结论:
若
则
向量的模等于其 x 坐标与 y 坐标的平方和的算术平方根.
例6. 设 a=(5, -7), b=(-6, -4), 求 a·b 及 a、b间的夹角q (精确到1?)
解:
5?(-6)+(-7)?(-4)
= -2.
cosq =
≈-0.03
查得q ≈92?.
解:
两点间的距离公式.
例(补充 ). 已知向量 的起点A(x1, y1), 终点 B (x2, y2), 求 和
结论:
设 A(x1, y1), B(x2, y2),
则 A、B 两点间的距离为
例(补充2). 设非零向量 a=(x1, y1), b=(x2, y2), 求证: a⊥b ? x1x2+y1y2=0.
证明:
若
则
即(x1, y1)·(x2, y2)=0,
得 x1x2+y1y2=0;
反之,
若 x1x2+y1y2=0,
即得
则
∴非零向量 成立.
结论:
设
则
?
x1x2+y1y2=0.
例5. 已知 A(1, 2), B(2, 3), C(-2, 5), 试判断△ABC的形状, 并给出证明.
证明:
= (1, 1),
= (-3, 3),
= 0,
则△ABC是直角三角形.
x
y
o
1
2
3
-2
5
2
A
B
C
解:
画出图形,
估计角A为直角,
△ABC为直角是角形.
例5. 已知 A(1, 2), B(2, 3), C(-2, 5), 试判断△ABC的形状, 并给出证明.
证明:
△ABC是直角三角形.
x
y
o
1
2
3
-2
5
2
A
B
C
解:
画出图形,
估计角A为直角,
△ABC为直角是角形.
得 |AB|2 + |AC|2 = |BC|2,
∵|AB|2 =
(2-1)2+(3-2)2
=2,
|AC|2 =
(-2-1)2+(5-2)2
=18,
|BC|2 =
(-2-2)2+(5-3)2
=20,
∴角A是直角,
法二, 用勾股定理判断:
练习: (课本107页)
第 1、2、3 题.
1. 已知 a=(-3, 4), b=(5, 2), 求 |a|, |b|, a·b.
练习: (课本107页)
解:
= -7.
= 5;
2. 已知 a=(2, 3), b=(-2, 4), c=(-1, -2). 求 a·b, (a+b)·(a-b), a·(b+c), (a+b)2.
解:
= 8;
= -7;
= 0;
(2, 3)·(-3, 2)
= -6+6
=22+32+2[2?(-2)+3?4)]+(-2)2+42
=49.
3. 已知 a=(3, 2), b=(5, -7), 利用计算器, 求 a 与 b 的夹角q (精确到1?).
解:
≈0.08,
查得q≈85?.
【课时小结】
1. 向量数量积的坐标表示
a=(x1, y1), b=(x2, y2),
a·b=(x1, y1)·(x2, y2)=x1x2+y1y2.
2. 两向量夹角的坐标表示
【课时小结】
3. 两向量垂直的坐标表示
a⊥b ?? x1x2+y1y2=0.
(a//b ?? x1y2-x2y1=0)
4. 向量的模
a=(x, y),
A(x1, y1), B(x2, y2)两点间距离:
习题2.4
第 5、9、10、11 题.
A 组
B 组
第 2、3、4、5 题.
5. 先作图, 观察以 A、B、C 为顶点的三角形的形状, 然后给出证明.
(1) A(-1, -4), B(5, 2), C(3, 4);
(2) A(-2, -3), B(19, 4), C(-1, -6);
(3) A(2, 5), B(5, 2), C(10, 7).
(1)
= 0.
则△ABC是直角三角形.
如图,
角B可能是直角.
x
y
o
3
4
-1
2
5
A
B
C
-4
证明:
习题2.4
A 组
5. 先作图, 观察以 A、B、C 为顶点的三角形的形状, 然后给出证明.
(1) A(-1, -4), B(5, 2), C(3, 4);
(2) A(-2, -3), B(19, 4), C(-1, -6);
(3) A(2, 5), B(5, 2), C(10, 7).
= 0.
则△ABC是直角三角形.
x
y
o
-1
19
-2
-6
4
A
B
C
-3
(2)
如图,
角A可能是直角.
证明:
习题2.4
A 组
= 0.
则△ABC是直角三角形.
5. 先作图, 观察以 A、B、C 为顶点的三角形的形状, 然后给出证明.
(1) A(-1, -4), B(5, 2), C(3, 4);
(2) A(-2, -3), B(19, 4), C(-1, -6);
(3) A(2, 5), B(5, 2), C(10, 7).
x
y
o
5
2
7
5
2
A
B
C
10
(3)
如图,
角B可能是直角.
证明:
习题2.4
A 组
9. 求证: A(1, 0), B(5, -2), C(8, 4), D(4, 6) 为顶点的四边形是一个矩形.
证明:
= 0.
则四边形ABCD是矩形.
即ABCD是□,
10. 已知 | a | = 3, b = (1, 2), 且a∥b, 求 a 的坐标.
解:
= l (1, 2)
= (l, 2l),
11. 已知a = (4, 2), 求与 a 垂直的单位向量的坐标.
解:
∴所求单位向量的坐标为:
解得
设所求单位向量的坐标为 (x, y),
则 x2+y2=1,
与 垂直得
4x+2y=0,
复习
提高
与
与
复
习
提高
返回目录
知识要点
1. 向量的数量积
a·b = |a|·|b|cosq = x1x2+y1y2.
2. 数量积的几何意义
q
D
O
C
A
B
=OC·OB
=OD·OA.
知识要点
3. 向量数量积的运算定律
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
知识要点
4. 两向量的垂直与共线
a⊥b ?? x1x2+y1y2=0.
a//b ?? b=la(l?R).
a//b ?? x1y2-x2y1=0
知识要点
5. 向量的模与两点间距离
a=(x, y),
A(x1, y1), B(x2, y2)两点间距离:
例题选讲
例1(习题2.3 B组第5题). 平面向量的数量积a·b是一个非常重要的概念, 利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
勾股定理:
证明:
则
由∠C=90?得
即
A
B
C
设△ABC中, ∠C=90?.
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
菱形对角线垂直:
证明:
则
A
B
C
D
= 0,
∴AC⊥BD.
设AC、BD为菱形ABCD的对角线.
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
长方形对角线相等:
证明:
A
B
C
D
又
设AC、BD为长方形ABCD的对角线.
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
正方形对角线垂直平分:
证明:
AC⊥BD;
A
B
C
D
O
同菱形的对角线垂直可证得
同勾股定理的证法可证得
即得 |AO| = |OC|,
同理得 |BO| = |OD|.
设AC、BD为正方形ABCD的对角线.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
如: 直角三角形斜边上的中线等于斜边的一半; 等腰三角形底边上的中线垂直于底边; 三角形的重心到顶点的距离等于到对边中点的距离的两倍等.
平行四边形的对角线互相平分; 平行四边形两对角线的平方和等于四边的平方和等.
在圆中, 连接弦的中点与圆心的直线垂直弦; 直径所对的圆周角是直角等.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
直角三角形斜边上的中线等于斜边的一半.
A
B
C
E
CE是Rt△ABC斜边AB的中线.
证明:
即CE = AB.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
等腰三角形底边上的中线垂直于底边.
AE是等腰△ABC底边BC上的中线.
证明:
A
B
C
E
∠CAE=∠BAE,
则AE⊥BC.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
三角形的重心到顶点的距离等于到对边中点的距离的两倍等.
G是△ABC中线AE与BF的交点.
证明:
A
B
C
E
F
G
设
用基底 表示
而
由
得方程组:
解得
即可得
GA=2GE,
GB=2GF.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
平行四边形的对角线互相平分.
AC、BD是□ABCD的对角线.
证明:
A
B
C
D
O
设
而
由
得方程组
1-m =l,
m =l,
解得
于是可得对角线互相平分.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
平行四边形两对角线平方和等于四边的平方和.
AC、BD是□ABCD的对角线.
证明:
A
B
C
D
O
即命题得证.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
在圆中, 连接弦的中点与圆心的直线垂直弦.
D是弦AB的中点, O为圆心.
证明:
A
B
D
O
·
∠BOD=∠DOA,
即OD⊥AB.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
直径所对的圆周角是直角等.
AB是⊙O的直径, C是圆上的点.
证明:
∴CB⊥CA,
A
B
C
O
·
又CO = AB,
即
①
②
由① = ② 得
得∠ACB=90?.
0,
返回目录
(共10题)
练
习
题
练习:
习题 2.4 B 组 第 1、2、3、4 题
补充练习:
1. 设 x, y?R, 向量 a=(x, 1), b=(1, y), c=(2, -4), 且 a⊥c, b//c, 则 |a+b|= ( )
(A) (B) (C) (D) 10
2. 平面向量 a 与 b 的夹角为60?, a=(2, 0), |b|=1, 则 |a+2b| 等于 ( )
(A) (B) (C) 4 (D) 12
3. 已知向量 a, b 夹角为 45?, 且 |a|=1, |2a-b| = 则 |b|= .
4. 已知向量 a, b 满足 |b|=2, a 与 b 的夹角为60?, 则 b 在 a 上的投影是 .
5. 设 a, b 是两个非零向量, ( )
(A) 若 |a+b|=|a|-|b|, 则 a⊥b
(B) 若 a⊥b, 则 |a+b|=|a|-|b|
(C) 若 |a+b|=|a|-|b|, 则存在实数 l, 使得 b=la
(D) 若存在实数 l, 使得 b=la, 则 |a+b|=|a|-|b|
6. 平面直角坐标系中, 点 O(0, 0), P(6, 8). 将向量 绕点 O 按逆时针方向
旋转 后, 得到向量 则点 Q 的坐标是 ( )
(A) (B) (C) (D)
1. 设 x, y?R, 向量 a=(x, 1), b=(1, y), c=(2, -4), 且 a⊥c, b//c, 则 |a+b|= ( )
(A) (B) (C) (D) 10
解:
由 得
2x-4=0.
由 得
-4-2y=0.
解得 x=2, y= -2.
则
=(3, -1).
B
2. 平面向量 a 与 b 的夹角为60?, a=(2, 0), |b|=1, 则 |a+2b| 等于 ( )
(A) (B) (C) 4 (D) 12
解:
由 得
则
B
3. 已知向量 a, b 夹角为 45?, 且 |a|=1, |2a-b|
= 则 |b|= .
解:
由 得
解得
4. 已知向量 a, b 满足 |b|=2, a 与 b 的夹角为60?, 则 b 在 a 上的投影是 .
解:
在 上的投影为
1
5. 设 a, b 是两个非零向量, ( )
(A) 若 |a+b|=|a|-|b|, 则 a⊥b
(B) 若 a⊥b, 则 |a+b|=|a|-|b|
(C) 若 |a+b|=|a|-|b|, 则存在实数 l, 使得 b=la
(D) 若存在实数 l, 使得 b=la, 则 |a+b|=|a|-|b|
解:
若
则
得 cosq = -1,
即 与 的夹角为180?, 与 共线.
∴C 选项正确.
C
6. 平面直角坐标系中, 点 O(0, 0), P(6, 8). 将
向量 绕点 O 按逆时针方向旋转 后, 得到向量
则点 Q 的坐标是 ( )
(A) (B)
(C) (D)
解:
由题设知,
与 的夹角为
设 Q(x, y),
则
解得
A
1. 已知 a 是非零向量, 且 b≠c, 求证: a·b=a·c ? a⊥(b-c).
证明:
由 得
反之,
则
得
即得
习题2.4 B 组
2. 如图, 在平面直角坐标系中, 以原点为圆心,单位长度为半径的圆上有两点A(cosa, sina), B(cosb, sinb), 试用A、B两点的坐标表示∠AOB 的余弦.
x
y
o
a
b
A
B
cos∠AOB =
= cosa cosb + sina sinb.
解:
3. 证明: 对于任意的 a、b、c、d?R, 恒有不等式
(ac+bd)2≤(a2+b2)(c2+d2).
分析:
ac+bd 类似于向量数量积 (a, b)·(c, d),
a2+b2、c2+d2 类似于向量的模的平方.
证明:
设
则
又
即
两边平方即得
(ac+bd)2≤(a2+b2)(c2+d2).
4. 如图, 在圆C中, 是不是只需知道圆C的半径或弦AB的长度, 就可以求 的值?
·
C
A
B
若只知道圆C的半径, 不能求
的值;
A
B
当AB为直径时,
=2r2,
当AB不是直径时,
∴只知道圆C的半径, 不能确定 的值.
答:
4. 如图, 在圆C中, 是不是只需知道圆C的半径或弦AB的长度, 就可以求 的值?
·
C
A
B
若知道弦长AB, 则可求
的值;
D
∴在圆C中只要知道弦AB的长, 即可求
答:
的值.
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
平面向量的数量积
2.4
2.4.1平面向量数量积的物理背景及其含义
复习与提高
2.4.2平面向量数量积的坐标表示、模、夹角
2.4.1
平面向量数量积
的
物理背景及其含义
返回目录
学习要点
1. 向量的数量积是怎样计算的? 它是一个向量还是一个数量?
2. 向量的数量积的几何意义是什么?
3. 两向量垂直的条件是什么?
4. 向量的数量积有哪些运算定律? 实数的运算定律是否有不适合向量的数量积的?
(一) 数量积的物理背景
在物理学中, 如果一个物体在力F 的作用下产生位移 s, 那么力F 所做的功为
W = | F |·| s | cosq,
其中 q 是 F 与 s 的夹角.
功W是一个标量, 它是由矢量 F 与 s 的运算结果.
为解决类似由矢量计算标量的问题, 数学中引入了向量的 “数量积” 概念.
s
F
q
(二) 向量的数量积
定义: 已知两个非零向量 a 和 b, 它们的夹角为q. 我们把数量 |a| |b|cosq 叫做 a 与 b 的数量积 (或内积), 记作 a·b, 即
a·b = |a| |b| cosq.
又规定: 零向量与任一向量的数量积为 0.
即两向量的数量积, 等于两向量的模与夹角的余弦的乘积.
练习: (课本106页)
第 1 题
补充练习
已知向量 |a|=1, |b|=2, a·b= . 则 a 与 b 的夹角 q = .
1. 已知 |p|=8, |q|=6, p 和 q 的夹角是60?, 求 p·q.
解:
= 24.
练习: (课本106页)
补充练习
已知向量 |a|=1, |b|=2, a·b= . 则 a 与 b 的夹角 q = .
解:
由 得
则 q =135?.
(常用形式)
135?
问题1. 向量的数量积与向量的数乘有什么区别? 向量的数量积是向量还是数量?
向量的数乘是一个向量, 而向量的数量积是一个数量, 是三个数量的乘积.
q
D
表示 在 方向上的投影 (如图),
几何意义:
O
C
A
B
表示 在 方向上的投影,
即
=OC·OB
=OD·OA.
例1. 已知 |a|=5, |b|=4, a 与 b 的夹角 q=120?, 求a·b 及 a 在 b 方向上的投影.
解:
= 5?4?cos120?
= -10.
在 方向上的投影为
=5cos120?
120?
O
C
OC即为 在 方向的投影.
(1)
当q =45?时,
O
A
(2)
当q =90?时,
(3)
当q =135?时,
O
(A)
(1)
(2)
(3)
O
A
解:
各图中的投影用OA表示.
45?
●
135?
3. 已知 |a|=6, e 为单位向量, 当 a、e 之间的夹角q 分别等于 45?、90?、135? 时, 画图表示 a 在 e 方向上的投影, 并求其值.
=0.
练习: (课本106页)
问题2. 非零向量 a 与 b 的数量积 a·b 在什么情况下为正? 在什么情况下这负? 在什么情况下为零?
即两向量的夹角为锐角时, 数量积为正,
夹角为钝角时, 数量积为负,
夹角为直角时, 数量积为零.
两非零向量垂直 ??数量积为零.
解:
2. 已知△ABC中, =a, =b, 当 a·b<0 或a·b=0 时, 试判断△ABC的形状.
当 时, cosA
< 0,
则角A为钝角,
∴△ABC为钝角三角形.
当 时, cosA
= 0,
则角A为直角,
∴△ABC为直角三角形.
两非零向量垂直??数量积为0.
练习: (课本106页)
(三) 数量积的运算律
问题3. 下列等式是否成立, 为什么?
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(5) (a·b)·c=a·(b·c).
分析:
(1)
(2)
同理
即 成立.
(三) 数量积的运算律
问题3. 下列等式是否成立, 为什么?
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(5) (a·b)·c=a·(b·c).
分析:
(3)
如图,
O
A
B
C
A?
B?
D
q2
q1
q3
=|OD|·|OC|,
=|OA?|·|OC|
+|A?D|·|OC|
=|OD|·|OC|,
(三) 数量积的运算律
问题3. 下列等式是否成立, 为什么?
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(5) (a·b)·c=a·(b·c).
分析:
(4)
即 成立.
(5)
是数乘向量,
与 共线,
也是数乘向量,
但与 共线,
两向量方向不一定相同, 所以不等.
数量积运算定律
例2. 类比实数的乘法公式, 下列向量等式是否成立?
(1) (a+b)2=a2+2ab+b2;
(2) (a+b)·(a-b)=a2-b2.
答: 两等式都成立.
∴(1)式成立.
又
∴(2)式成立.
实数的乘法公式适用向量的乘法运算.
例3. 已知 |a|=6, |b|=4, a 与 b 的夹角为 60?, 求 (a+2b)·(a-3b).
解:
例4. 已知 | a |=3, | b |=4, 且 a 与 b 不共线. k 为何值时, 向量 a+kb 与 a-kb 互相垂直?
解:
两向量垂直, 其数量积为零,
= 9-16k2,
两使 9-16k2 = 0,
解得
答: 当k = 时, 向量 互相垂直.
【课时小结】
1. 向量的数量积
2. 数量积的几何意义
一个向量在另一个向量方向上的投影.
q
D
O
C
A
B
即
=OC·OB
=OD·OA.
【课时小结】
3. 向量数量积的运算定律
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(a·b)·c≠a·(b·c).
注意:
实数的乘法交换律不适应.
【课时小结】
4. 有关数量积的计算
(1) 求夹角
(2) 两非零向量垂直
(3) 两向量共线
(4) 模
习题 2.4
A 组
第 2、3、6、7、8 题.
2. 已知△ABC中, a=5, b=8, C=60?, 求
解:
(如图)
A
B
C
120?
= 120?,
= -20.
习题 2.4
A 组
3. 已知 |a|=2, |b|=5, a·b= -3, 求 |a+b|, |a-b|.
解:
解:
得 q =135?.
注意
6. 设 |a|=12, |b|=9, a·b= 求 a 与 b 的夹角q.
7. 已知 |a|=4, |b|=3, (2a-3b)·(2a+b)=61, 求 a 与b 的夹角q.
解:
由 得
64-48cosq -27=61,
解得 cosq =
得 q =120?.
8. 已知 |a|=8, |b|=10, |a+b|=16, 求 a 与 b 的夹角q (精确到1?). (可用计算器)
解:
由 得
解得cosq =
得q≈55?.
2.4.2
平
面
向
量
数
量
积
的
坐
标
表
示
模
夹
角
返回目录
学习要点
1. 用坐标表示的向量怎样计算两向量的数量积? 怎样计算两向量的夹角?
2. 用坐标表示的向量怎样计算它的模?
3. 两向量垂直时, 其坐标满足什么条件? 与两向量共线的条件有什么区别?
思考题. 已知向量 a = (x1, y1), b = (x2, y2), 用坐标怎样表示 a·b? (提示: 用 x、y 轴正方向的单位向量作基底)
分析:
设 表示 x、y 轴正方向的单位向量,
∴上式=
则
这就是向量数量积的坐标表示.
即 (x1, y1)·(x2, y2) =x1x2+y1y2.
结论:
两个向量的数量积等于它们对应坐标的乘积的和.
练习: (补充)
1. 已知向量 a、b 的坐标表示如下,求 a · b.
(1) a = (3, -1), b = (-2, -5);
(2) a = (3, -1), b = (-1, -3);
(3) a = (1, 0), b = (1, 1).
2. 设向量 a = (x, y), 求 a2 和 | a | .
解: (1)
= -6+5
= -1;
(2)
= -3+3
= 0;
= 1.
(3)
1. 已知向量 a、b 的坐标表示如下,求a · b.
(1) a = (3, -1), b = (-2, -5);
(2) a = (3, -1), b = (-1, -3);
(3) a = (1, 0), b = (1, 1).
练习: (补充)
2. 设向量 a = (x, y), 求 a2 和 | a | .
解:
结论:
若
则
向量的模等于其 x 坐标与 y 坐标的平方和的算术平方根.
例6. 设 a=(5, -7), b=(-6, -4), 求 a·b 及 a、b间的夹角q (精确到1?)
解:
5?(-6)+(-7)?(-4)
= -2.
cosq =
≈-0.03
查得q ≈92?.
解:
两点间的距离公式.
例(补充 ). 已知向量 的起点A(x1, y1), 终点 B (x2, y2), 求 和
结论:
设 A(x1, y1), B(x2, y2),
则 A、B 两点间的距离为
例(补充2). 设非零向量 a=(x1, y1), b=(x2, y2), 求证: a⊥b ? x1x2+y1y2=0.
证明:
若
则
即(x1, y1)·(x2, y2)=0,
得 x1x2+y1y2=0;
反之,
若 x1x2+y1y2=0,
即得
则
∴非零向量 成立.
结论:
设
则
?
x1x2+y1y2=0.
例5. 已知 A(1, 2), B(2, 3), C(-2, 5), 试判断△ABC的形状, 并给出证明.
证明:
= (1, 1),
= (-3, 3),
= 0,
则△ABC是直角三角形.
x
y
o
1
2
3
-2
5
2
A
B
C
解:
画出图形,
估计角A为直角,
△ABC为直角是角形.
例5. 已知 A(1, 2), B(2, 3), C(-2, 5), 试判断△ABC的形状, 并给出证明.
证明:
△ABC是直角三角形.
x
y
o
1
2
3
-2
5
2
A
B
C
解:
画出图形,
估计角A为直角,
△ABC为直角是角形.
得 |AB|2 + |AC|2 = |BC|2,
∵|AB|2 =
(2-1)2+(3-2)2
=2,
|AC|2 =
(-2-1)2+(5-2)2
=18,
|BC|2 =
(-2-2)2+(5-3)2
=20,
∴角A是直角,
法二, 用勾股定理判断:
练习: (课本107页)
第 1、2、3 题.
1. 已知 a=(-3, 4), b=(5, 2), 求 |a|, |b|, a·b.
练习: (课本107页)
解:
= -7.
= 5;
2. 已知 a=(2, 3), b=(-2, 4), c=(-1, -2). 求 a·b, (a+b)·(a-b), a·(b+c), (a+b)2.
解:
= 8;
= -7;
= 0;
(2, 3)·(-3, 2)
= -6+6
=22+32+2[2?(-2)+3?4)]+(-2)2+42
=49.
3. 已知 a=(3, 2), b=(5, -7), 利用计算器, 求 a 与 b 的夹角q (精确到1?).
解:
≈0.08,
查得q≈85?.
【课时小结】
1. 向量数量积的坐标表示
a=(x1, y1), b=(x2, y2),
a·b=(x1, y1)·(x2, y2)=x1x2+y1y2.
2. 两向量夹角的坐标表示
【课时小结】
3. 两向量垂直的坐标表示
a⊥b ?? x1x2+y1y2=0.
(a//b ?? x1y2-x2y1=0)
4. 向量的模
a=(x, y),
A(x1, y1), B(x2, y2)两点间距离:
习题2.4
第 5、9、10、11 题.
A 组
B 组
第 2、3、4、5 题.
5. 先作图, 观察以 A、B、C 为顶点的三角形的形状, 然后给出证明.
(1) A(-1, -4), B(5, 2), C(3, 4);
(2) A(-2, -3), B(19, 4), C(-1, -6);
(3) A(2, 5), B(5, 2), C(10, 7).
(1)
= 0.
则△ABC是直角三角形.
如图,
角B可能是直角.
x
y
o
3
4
-1
2
5
A
B
C
-4
证明:
习题2.4
A 组
5. 先作图, 观察以 A、B、C 为顶点的三角形的形状, 然后给出证明.
(1) A(-1, -4), B(5, 2), C(3, 4);
(2) A(-2, -3), B(19, 4), C(-1, -6);
(3) A(2, 5), B(5, 2), C(10, 7).
= 0.
则△ABC是直角三角形.
x
y
o
-1
19
-2
-6
4
A
B
C
-3
(2)
如图,
角A可能是直角.
证明:
习题2.4
A 组
= 0.
则△ABC是直角三角形.
5. 先作图, 观察以 A、B、C 为顶点的三角形的形状, 然后给出证明.
(1) A(-1, -4), B(5, 2), C(3, 4);
(2) A(-2, -3), B(19, 4), C(-1, -6);
(3) A(2, 5), B(5, 2), C(10, 7).
x
y
o
5
2
7
5
2
A
B
C
10
(3)
如图,
角B可能是直角.
证明:
习题2.4
A 组
9. 求证: A(1, 0), B(5, -2), C(8, 4), D(4, 6) 为顶点的四边形是一个矩形.
证明:
= 0.
则四边形ABCD是矩形.
即ABCD是□,
10. 已知 | a | = 3, b = (1, 2), 且a∥b, 求 a 的坐标.
解:
= l (1, 2)
= (l, 2l),
11. 已知a = (4, 2), 求与 a 垂直的单位向量的坐标.
解:
∴所求单位向量的坐标为:
解得
设所求单位向量的坐标为 (x, y),
则 x2+y2=1,
与 垂直得
4x+2y=0,
复习
提高
与
与
复
习
提高
返回目录
知识要点
1. 向量的数量积
a·b = |a|·|b|cosq = x1x2+y1y2.
2. 数量积的几何意义
q
D
O
C
A
B
=OC·OB
=OD·OA.
知识要点
3. 向量数量积的运算定律
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
知识要点
4. 两向量的垂直与共线
a⊥b ?? x1x2+y1y2=0.
a//b ?? b=la(l?R).
a//b ?? x1y2-x2y1=0
知识要点
5. 向量的模与两点间距离
a=(x, y),
A(x1, y1), B(x2, y2)两点间距离:
例题选讲
例1(习题2.3 B组第5题). 平面向量的数量积a·b是一个非常重要的概念, 利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
勾股定理:
证明:
则
由∠C=90?得
即
A
B
C
设△ABC中, ∠C=90?.
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
菱形对角线垂直:
证明:
则
A
B
C
D
= 0,
∴AC⊥BD.
设AC、BD为菱形ABCD的对角线.
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
长方形对角线相等:
证明:
A
B
C
D
又
设AC、BD为长方形ABCD的对角线.
5. 平面向量的数量积a·b是一个非常重要的概念,利用它可以容易地证明平面几何的很多命题, 例如勾股定理、菱形对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等, 请你给出具体证明.
正方形对角线垂直平分:
证明:
AC⊥BD;
A
B
C
D
O
同菱形的对角线垂直可证得
同勾股定理的证法可证得
即得 |AO| = |OC|,
同理得 |BO| = |OD|.
设AC、BD为正方形ABCD的对角线.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
如: 直角三角形斜边上的中线等于斜边的一半; 等腰三角形底边上的中线垂直于底边; 三角形的重心到顶点的距离等于到对边中点的距离的两倍等.
平行四边形的对角线互相平分; 平行四边形两对角线的平方和等于四边的平方和等.
在圆中, 连接弦的中点与圆心的直线垂直弦; 直径所对的圆周角是直角等.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
直角三角形斜边上的中线等于斜边的一半.
A
B
C
E
CE是Rt△ABC斜边AB的中线.
证明:
即CE = AB.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
等腰三角形底边上的中线垂直于底边.
AE是等腰△ABC底边BC上的中线.
证明:
A
B
C
E
∠CAE=∠BAE,
则AE⊥BC.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
三角形的重心到顶点的距离等于到对边中点的距离的两倍等.
G是△ABC中线AE与BF的交点.
证明:
A
B
C
E
F
G
设
用基底 表示
而
由
得方程组:
解得
即可得
GA=2GE,
GB=2GF.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
平行四边形的对角线互相平分.
AC、BD是□ABCD的对角线.
证明:
A
B
C
D
O
设
而
由
得方程组
1-m =l,
m =l,
解得
于是可得对角线互相平分.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
平行四边形两对角线平方和等于四边的平方和.
AC、BD是□ABCD的对角线.
证明:
A
B
C
D
O
即命题得证.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
在圆中, 连接弦的中点与圆心的直线垂直弦.
D是弦AB的中点, O为圆心.
证明:
A
B
D
O
·
∠BOD=∠DOA,
即OD⊥AB.
你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗?
直径所对的圆周角是直角等.
AB是⊙O的直径, C是圆上的点.
证明:
∴CB⊥CA,
A
B
C
O
·
又CO = AB,
即
①
②
由① = ② 得
得∠ACB=90?.
0,
返回目录
(共10题)
练
习
题
练习:
习题 2.4 B 组 第 1、2、3、4 题
补充练习:
1. 设 x, y?R, 向量 a=(x, 1), b=(1, y), c=(2, -4), 且 a⊥c, b//c, 则 |a+b|= ( )
(A) (B) (C) (D) 10
2. 平面向量 a 与 b 的夹角为60?, a=(2, 0), |b|=1, 则 |a+2b| 等于 ( )
(A) (B) (C) 4 (D) 12
3. 已知向量 a, b 夹角为 45?, 且 |a|=1, |2a-b| = 则 |b|= .
4. 已知向量 a, b 满足 |b|=2, a 与 b 的夹角为60?, 则 b 在 a 上的投影是 .
5. 设 a, b 是两个非零向量, ( )
(A) 若 |a+b|=|a|-|b|, 则 a⊥b
(B) 若 a⊥b, 则 |a+b|=|a|-|b|
(C) 若 |a+b|=|a|-|b|, 则存在实数 l, 使得 b=la
(D) 若存在实数 l, 使得 b=la, 则 |a+b|=|a|-|b|
6. 平面直角坐标系中, 点 O(0, 0), P(6, 8). 将向量 绕点 O 按逆时针方向
旋转 后, 得到向量 则点 Q 的坐标是 ( )
(A) (B) (C) (D)
1. 设 x, y?R, 向量 a=(x, 1), b=(1, y), c=(2, -4), 且 a⊥c, b//c, 则 |a+b|= ( )
(A) (B) (C) (D) 10
解:
由 得
2x-4=0.
由 得
-4-2y=0.
解得 x=2, y= -2.
则
=(3, -1).
B
2. 平面向量 a 与 b 的夹角为60?, a=(2, 0), |b|=1, 则 |a+2b| 等于 ( )
(A) (B) (C) 4 (D) 12
解:
由 得
则
B
3. 已知向量 a, b 夹角为 45?, 且 |a|=1, |2a-b|
= 则 |b|= .
解:
由 得
解得
4. 已知向量 a, b 满足 |b|=2, a 与 b 的夹角为60?, 则 b 在 a 上的投影是 .
解:
在 上的投影为
1
5. 设 a, b 是两个非零向量, ( )
(A) 若 |a+b|=|a|-|b|, 则 a⊥b
(B) 若 a⊥b, 则 |a+b|=|a|-|b|
(C) 若 |a+b|=|a|-|b|, 则存在实数 l, 使得 b=la
(D) 若存在实数 l, 使得 b=la, 则 |a+b|=|a|-|b|
解:
若
则
得 cosq = -1,
即 与 的夹角为180?, 与 共线.
∴C 选项正确.
C
6. 平面直角坐标系中, 点 O(0, 0), P(6, 8). 将
向量 绕点 O 按逆时针方向旋转 后, 得到向量
则点 Q 的坐标是 ( )
(A) (B)
(C) (D)
解:
由题设知,
与 的夹角为
设 Q(x, y),
则
解得
A
1. 已知 a 是非零向量, 且 b≠c, 求证: a·b=a·c ? a⊥(b-c).
证明:
由 得
反之,
则
得
即得
习题2.4 B 组
2. 如图, 在平面直角坐标系中, 以原点为圆心,单位长度为半径的圆上有两点A(cosa, sina), B(cosb, sinb), 试用A、B两点的坐标表示∠AOB 的余弦.
x
y
o
a
b
A
B
cos∠AOB =
= cosa cosb + sina sinb.
解:
3. 证明: 对于任意的 a、b、c、d?R, 恒有不等式
(ac+bd)2≤(a2+b2)(c2+d2).
分析:
ac+bd 类似于向量数量积 (a, b)·(c, d),
a2+b2、c2+d2 类似于向量的模的平方.
证明:
设
则
又
即
两边平方即得
(ac+bd)2≤(a2+b2)(c2+d2).
4. 如图, 在圆C中, 是不是只需知道圆C的半径或弦AB的长度, 就可以求 的值?
·
C
A
B
若只知道圆C的半径, 不能求
的值;
A
B
当AB为直径时,
=2r2,
当AB不是直径时,
∴只知道圆C的半径, 不能确定 的值.
答:
4. 如图, 在圆C中, 是不是只需知道圆C的半径或弦AB的长度, 就可以求 的值?
·
C
A
B
若知道弦长AB, 则可求
的值;
D
∴在圆C中只要知道弦AB的长, 即可求
答:
的值.
