8.4三元一次方程组的解法课件(24张)
文档属性
| 名称 | 8.4三元一次方程组的解法课件(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 280.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 15:27:02 | ||
图片预览








文档简介
(共24张PPT)
第八章
二元一次方程组
8.4
三元一次方程组的解法
1.熟练掌握解三元一次方程组的方法与步骤,会解简单的三元一次方程组.
2.会用代入法或加减法解三元一次方程组.
学习目标
课堂导入
这样的方程组我们叫它什么呢,该怎样解呢?
小明手头有12张面额分别是1元、2元和5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍。求1元、2元和5元的纸币各多少张?
设1元、2元、5元的纸币分别为x张、y张、z张
新知讲解
三元一次方程组
特点:(1)方程组中含有三个未知数;
(2)每个方程中含有未知数得项的次数都为1;
(3)方程组中一共有三个方程。
含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。
三元一次方程组的解
解方程组:
(1)用代入消元法解:
将③代入①、②,得
新知讲解
三元一次方程组的解
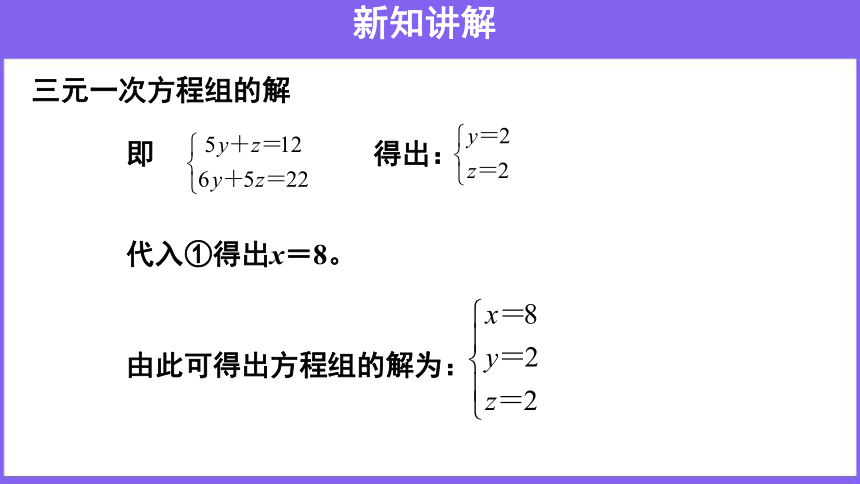
即
得出:
代入①得出x=8。
由此可得出方程组的解为:
新知讲解
三元一次方程组的解
解方程组:
用加减消元法解这个方程组
①×5-②,得4x+3y=38.④
新知讲解
三元一次方程组的解
③与④组成方程组
解这个方程组,得
代入①式得z=2,
由此可得出方程组的解为:
新知讲解
总结
解三元一次方程组的基本思路是:通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。
新知讲解
典型例题
例1:解方程组:
解析:观察各个方程的特点,可以考虑用加减法求解。
解:
解:
由①+③,②+2×③消去z得
解得
代入①得z=3.
即原方程组的解为
典型例题
例2:解下列三元一次方程组:
解析:观察各个方程的特点,可以考虑用代入法求解,将①分别代入②和③中,消去z可得到关于x、y的二元一次方程组。
典型例题
解:
将①代入②、③,消去z,得
解得
把x=2,y=3代入①,得z=5。
所以原方程组的解为
典型例题
例2:若|a-b-1|+(b-2a+c)2+|2c-b|=0,求a,b,c的值。
解析:本题考查非负数性质的综合应用,要使等式成立必须使每个非负数都为0。
典型例题
解:
因为三个非负数的和等于0,所以每个非负数都为0。
可得方程组
解得
所以a=-3,b=-4,c=-2。
典型例题
随堂练习
1.
下列方程组中,是三元一次方程组的是(
)
D
A.
B.
C.
D.
2.
解方程组:
①-②,得x+2y=11.④
解:
①+③,得5x+2y=9.⑤
④与⑤组成方程组
随堂练习
解:
解得
所以原方程组的解是
把x=-
,y=
代入②,得z=-
。
随堂练习
3.
已知有理数x、y、z满足条件|x-z-2|+|3x-6y-7|+(3y+3z-4)2=0,求xyz的值。
解:依题意有
解得
所以xyz=3×
×1=1。
随堂练习
4.
某区中学足球赛共赛8轮,胜一场得3分,平一场得1分,负一场得0分,在这次足球联赛中,猛虎足球队平的场数是所负场数的2倍,共得17分,试问该队胜了几场?
解:
设猛虎足球队胜了x场,平了y场,负了z场,依题意得
随堂练习
解:
答:该队胜了5场。
解得
随堂练习
含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。
课堂小结
再
见
第八章
二元一次方程组
8.4
三元一次方程组的解法
1.熟练掌握解三元一次方程组的方法与步骤,会解简单的三元一次方程组.
2.会用代入法或加减法解三元一次方程组.
学习目标
课堂导入
这样的方程组我们叫它什么呢,该怎样解呢?
小明手头有12张面额分别是1元、2元和5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍。求1元、2元和5元的纸币各多少张?
设1元、2元、5元的纸币分别为x张、y张、z张
新知讲解
三元一次方程组
特点:(1)方程组中含有三个未知数;
(2)每个方程中含有未知数得项的次数都为1;
(3)方程组中一共有三个方程。
含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。
三元一次方程组的解
解方程组:
(1)用代入消元法解:
将③代入①、②,得
新知讲解
三元一次方程组的解
即
得出:
代入①得出x=8。
由此可得出方程组的解为:
新知讲解
三元一次方程组的解
解方程组:
用加减消元法解这个方程组
①×5-②,得4x+3y=38.④
新知讲解
三元一次方程组的解
③与④组成方程组
解这个方程组,得
代入①式得z=2,
由此可得出方程组的解为:
新知讲解
总结
解三元一次方程组的基本思路是:通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。
新知讲解
典型例题
例1:解方程组:
解析:观察各个方程的特点,可以考虑用加减法求解。
解:
解:
由①+③,②+2×③消去z得
解得
代入①得z=3.
即原方程组的解为
典型例题
例2:解下列三元一次方程组:
解析:观察各个方程的特点,可以考虑用代入法求解,将①分别代入②和③中,消去z可得到关于x、y的二元一次方程组。
典型例题
解:
将①代入②、③,消去z,得
解得
把x=2,y=3代入①,得z=5。
所以原方程组的解为
典型例题
例2:若|a-b-1|+(b-2a+c)2+|2c-b|=0,求a,b,c的值。
解析:本题考查非负数性质的综合应用,要使等式成立必须使每个非负数都为0。
典型例题
解:
因为三个非负数的和等于0,所以每个非负数都为0。
可得方程组
解得
所以a=-3,b=-4,c=-2。
典型例题
随堂练习
1.
下列方程组中,是三元一次方程组的是(
)
D
A.
B.
C.
D.
2.
解方程组:
①-②,得x+2y=11.④
解:
①+③,得5x+2y=9.⑤
④与⑤组成方程组
随堂练习
解:
解得
所以原方程组的解是
把x=-
,y=
代入②,得z=-
。
随堂练习
3.
已知有理数x、y、z满足条件|x-z-2|+|3x-6y-7|+(3y+3z-4)2=0,求xyz的值。
解:依题意有
解得
所以xyz=3×
×1=1。
随堂练习
4.
某区中学足球赛共赛8轮,胜一场得3分,平一场得1分,负一场得0分,在这次足球联赛中,猛虎足球队平的场数是所负场数的2倍,共得17分,试问该队胜了几场?
解:
设猛虎足球队胜了x场,平了y场,负了z场,依题意得
随堂练习
解:
答:该队胜了5场。
解得
随堂练习
含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。
课堂小结
再
见
