数学人教版(2019)必修一4.5.2用二分法求方程的近似解(共23张ppt)
文档属性
| 名称 | 数学人教版(2019)必修一4.5.2用二分法求方程的近似解(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 731.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 21:30:06 | ||
图片预览








文档简介
(共23张PPT)
《用二分法求方程的近似解》
学习目标:
一、复习导入
1、零点的定义:
函数
y=f(x)
,我们把使
f(x)=0
的
实数x
叫做函数
y=f(x)
的零点。
2、结论:方程
f(x)=0
有实数根
函数
y=f(x)
的图像与x轴有公共点
函数
y=f(x)
有零点
3、零点存在性判定定理
二、考一考:
①认真观察下面两个方程,求出方程的根
你能求出方程的近似解吗
如何找到零点近似值
?
可以转化为函数
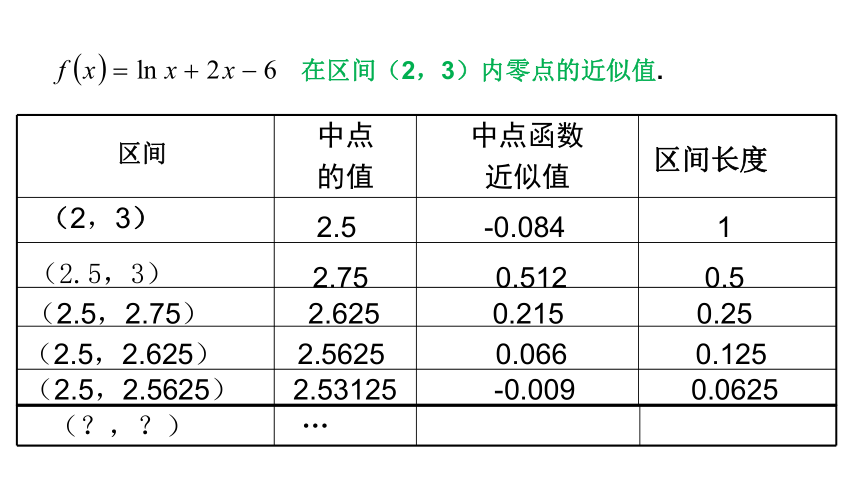
在区间(2,3)内零点的近似值。
②思考:求方程
的近似解的问题
三、情境导入
1.现有一根长160米的线路,在某处存在一个故障点,线路上均匀分布着17根电线杆,现只有一段11米长的导线可供替换,假如你是一名电工,你将如何高效、合理的解决这一问题?
2.经济频道某节目,游戏规则:某掌上电脑的价格在600—3000元之间,猜测它的价格,猜对了就是你的了。每次猜后主持人会给出“多了”还是“少了”的提示,在10秒内且误差不超过5元时算猜对。
3.请每位同学从(0,64)中任选一个整数,记在心里,我提六个问题,你只要回答我“高了”还是“低了”。六个问题全答完以后,我就会算出你心里记的那个数。
小组讨论交流,如何逐步缩小故障点范围、猜出掌上电脑的价格和你心中的那个数?采取的方法是什么?具体如何操作?说出你的方案设计。
问题:
四、新知探究
绘制函数图像
在区间(2,3)内零点的近似值.
中点
的值
中点函数
近似值
(2,3)
(2.5,2.75)
(2.5,2.5625)
2.5
2.75
2.625
2.5625
(2.5,2.625)
-0.084
0.512
0.215
0.066
1
0.5
0.25
0.125
0.0625
(2.5,3)
区间长度
区间
2.53125
-0.009
(?,?)
…
思考1:
通过不断的取中点,逐步缩小零点所在区间范围,区间缩小到什么程度,才能终止运算?
可以加上一个什么条件?
思考2:
精确度?的含义
思考3:
精确度为0.1,0.01
时,零点近似值分别是多少?
精确度为0.01,即零点值与近似值的差的绝对值要小于或等于0.01
区间
中点的值
中点函数
近似值
区间长度
(2,3)
(2.5,3)
(2.5,2.75)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
2.5
2.75
2.625
2.5625
2.53125
2.546875
(2.5,2.625)
2.5390625
2.53515625
-0.084
0.512
0.215
0.066
-0.009
0.029
0.010
0.001
1
0.5
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
(精确度为0.01)
对于在区间
上连续不断且
的函
数
,通过不断地把函数
的零点所在的区
间一分为二,使区间的两个端点逐步逼近零点,进而得到
零点近似值的方法叫做二分法.
二分法概念
x
y
0
a
b
五、概念形成
练习:
通过下列函数的图象,判断不能用“二分法”求其零点的是(
)
(A)①②③
(B)②③④
(C)①②④
(D)①③④
C
解析:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)·f(b)<0,由图象可得,只有③能满足此条件,故不能用“二分法”求其零点的是①②④,故选C.
二分法的实质:
就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.
思考:
你能归纳出“给定精确度ε,用二分法求函数零点近似值的步骤”吗?
思考1:怎样确定零点的范围?
零点落在异号间!
思考2:如何最快的缩小零点所在的范围?
取中点
思考3:如何理解误差不超过0.1?
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·
f(c)<0,则令b=
c(此时零点x0∈(a,
c)
);
(3)若f(c)·
f(b)<0,则令a=
c(此时零点x0∈(
c,
b)
).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
六、归纳总结及应用:
周而复始怎么办?
定区间,找中点,
零点落在异号间,
口
诀
中值计算两边看;
区间长度缩一半;
精确度上来判断.
归纳总结:
0
1
2
3
4
6
5
7
8
-6
-2
3
10
21
40
75
142
273
列表
尝试:
例2:借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).
先确定零点的范围;再用二分法去求方程的近似解
绘制函数图像
区间
中点的值
中点函数近似值
(1,2)
由于
|1.375-1.4375|=0.0625<0.1
所以原方程的近似解为1.4375。
1.5
0.33
1.25
1.375
-0.28
-0.87
1.4375
0.02
(1,1.5)
(1.25,1.5)
(1.375,1.5)
(1.375,1.4375)
拓展:若要求精确度为0.01,你知道至少需要执行几次“二分”操作吗?
二分法计算近似值
巩固练习:
1、用二分法求函数
在
内零点近似值的过程中得
则函数的零点落在区间(
)
A.
B.
C.不能确定
B
2、先用求根公式求方程x2-5=0的解,然后借助计算器用二分法求函数f(x)=x2-5在区间(-3,-2)内的近似解(精确度0.1).
分析:先确定f(-2)与f(-3)的符号,再按照二分法求函数零点近似值的步骤求解.
解:由于f(-2)=-1<0,f(-3)=4>0,故取区间[-3,-2]作为计算的初始区间.用二分法逐次计算,列表如下:
由于|-2.25-(-2.187
5)|=0.062
5<0.1,
所以函数的一个近似负零点可取-2.25.
七、课堂总结:
通过本节课的学习,你在知识和数学思想方面有哪些收获?小组讨论交流,说一说自己的收获。
1.知识方面:
二分法
用二分法求方程近似解的步骤
2.数学思想方法:
函数与方程思想
逼近思想
类比方法
八、分层作业
基础巩固题
1、课本P155
复习巩固4、5
2、阅读课本P147《中外历史上的方程求解》拓展
提高题
3、课本P156
综合应用8
谢谢观看!
《用二分法求方程的近似解》
学习目标:
一、复习导入
1、零点的定义:
函数
y=f(x)
,我们把使
f(x)=0
的
实数x
叫做函数
y=f(x)
的零点。
2、结论:方程
f(x)=0
有实数根
函数
y=f(x)
的图像与x轴有公共点
函数
y=f(x)
有零点
3、零点存在性判定定理
二、考一考:
①认真观察下面两个方程,求出方程的根
你能求出方程的近似解吗
如何找到零点近似值
?
可以转化为函数
在区间(2,3)内零点的近似值。
②思考:求方程
的近似解的问题
三、情境导入
1.现有一根长160米的线路,在某处存在一个故障点,线路上均匀分布着17根电线杆,现只有一段11米长的导线可供替换,假如你是一名电工,你将如何高效、合理的解决这一问题?
2.经济频道某节目,游戏规则:某掌上电脑的价格在600—3000元之间,猜测它的价格,猜对了就是你的了。每次猜后主持人会给出“多了”还是“少了”的提示,在10秒内且误差不超过5元时算猜对。
3.请每位同学从(0,64)中任选一个整数,记在心里,我提六个问题,你只要回答我“高了”还是“低了”。六个问题全答完以后,我就会算出你心里记的那个数。
小组讨论交流,如何逐步缩小故障点范围、猜出掌上电脑的价格和你心中的那个数?采取的方法是什么?具体如何操作?说出你的方案设计。
问题:
四、新知探究
绘制函数图像
在区间(2,3)内零点的近似值.
中点
的值
中点函数
近似值
(2,3)
(2.5,2.75)
(2.5,2.5625)
2.5
2.75
2.625
2.5625
(2.5,2.625)
-0.084
0.512
0.215
0.066
1
0.5
0.25
0.125
0.0625
(2.5,3)
区间长度
区间
2.53125
-0.009
(?,?)
…
思考1:
通过不断的取中点,逐步缩小零点所在区间范围,区间缩小到什么程度,才能终止运算?
可以加上一个什么条件?
思考2:
精确度?的含义
思考3:
精确度为0.1,0.01
时,零点近似值分别是多少?
精确度为0.01,即零点值与近似值的差的绝对值要小于或等于0.01
区间
中点的值
中点函数
近似值
区间长度
(2,3)
(2.5,3)
(2.5,2.75)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
2.5
2.75
2.625
2.5625
2.53125
2.546875
(2.5,2.625)
2.5390625
2.53515625
-0.084
0.512
0.215
0.066
-0.009
0.029
0.010
0.001
1
0.5
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
(精确度为0.01)
对于在区间
上连续不断且
的函
数
,通过不断地把函数
的零点所在的区
间一分为二,使区间的两个端点逐步逼近零点,进而得到
零点近似值的方法叫做二分法.
二分法概念
x
y
0
a
b
五、概念形成
练习:
通过下列函数的图象,判断不能用“二分法”求其零点的是(
)
(A)①②③
(B)②③④
(C)①②④
(D)①③④
C
解析:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)·f(b)<0,由图象可得,只有③能满足此条件,故不能用“二分法”求其零点的是①②④,故选C.
二分法的实质:
就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.
思考:
你能归纳出“给定精确度ε,用二分法求函数零点近似值的步骤”吗?
思考1:怎样确定零点的范围?
零点落在异号间!
思考2:如何最快的缩小零点所在的范围?
取中点
思考3:如何理解误差不超过0.1?
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·
f(c)<0,则令b=
c(此时零点x0∈(a,
c)
);
(3)若f(c)·
f(b)<0,则令a=
c(此时零点x0∈(
c,
b)
).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
六、归纳总结及应用:
周而复始怎么办?
定区间,找中点,
零点落在异号间,
口
诀
中值计算两边看;
区间长度缩一半;
精确度上来判断.
归纳总结:
0
1
2
3
4
6
5
7
8
-6
-2
3
10
21
40
75
142
273
列表
尝试:
例2:借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).
先确定零点的范围;再用二分法去求方程的近似解
绘制函数图像
区间
中点的值
中点函数近似值
(1,2)
由于
|1.375-1.4375|=0.0625<0.1
所以原方程的近似解为1.4375。
1.5
0.33
1.25
1.375
-0.28
-0.87
1.4375
0.02
(1,1.5)
(1.25,1.5)
(1.375,1.5)
(1.375,1.4375)
拓展:若要求精确度为0.01,你知道至少需要执行几次“二分”操作吗?
二分法计算近似值
巩固练习:
1、用二分法求函数
在
内零点近似值的过程中得
则函数的零点落在区间(
)
A.
B.
C.不能确定
B
2、先用求根公式求方程x2-5=0的解,然后借助计算器用二分法求函数f(x)=x2-5在区间(-3,-2)内的近似解(精确度0.1).
分析:先确定f(-2)与f(-3)的符号,再按照二分法求函数零点近似值的步骤求解.
解:由于f(-2)=-1<0,f(-3)=4>0,故取区间[-3,-2]作为计算的初始区间.用二分法逐次计算,列表如下:
由于|-2.25-(-2.187
5)|=0.062
5<0.1,
所以函数的一个近似负零点可取-2.25.
七、课堂总结:
通过本节课的学习,你在知识和数学思想方面有哪些收获?小组讨论交流,说一说自己的收获。
1.知识方面:
二分法
用二分法求方程近似解的步骤
2.数学思想方法:
函数与方程思想
逼近思想
类比方法
八、分层作业
基础巩固题
1、课本P155
复习巩固4、5
2、阅读课本P147《中外历史上的方程求解》拓展
提高题
3、课本P156
综合应用8
谢谢观看!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
