湘教版八年级数学下册2.4三角形的中位线课件(18张)
文档属性
| 名称 | 湘教版八年级数学下册2.4三角形的中位线课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 594.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
三角形的中位线
A
B
C
D
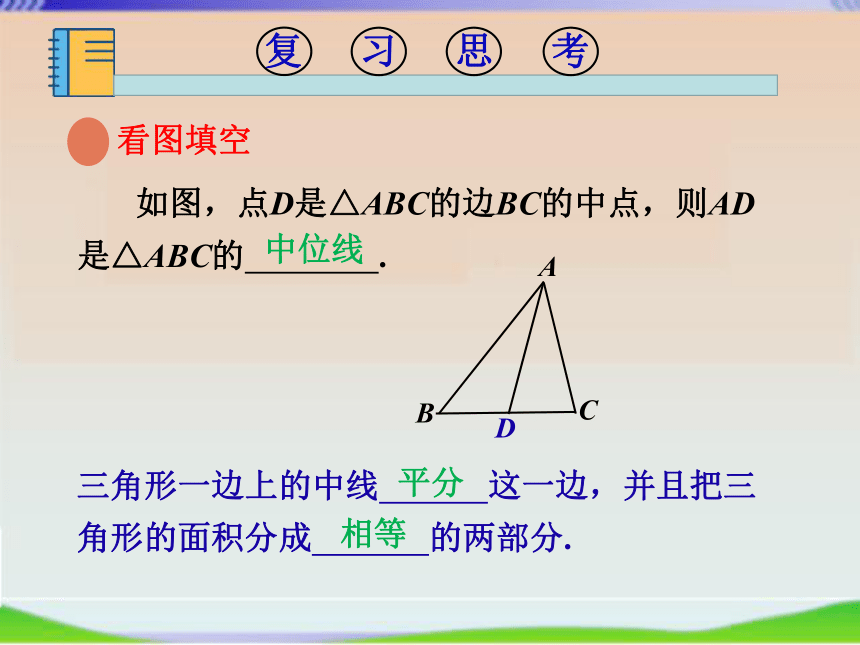
如图,点D是△ABC的边BC的中点,则AD是△ABC的
.
三角形一边上的中线
这一边,并且把三角形的面积分成
的两部分.
看图填空
中位线
平分
相等
复
习
思
考
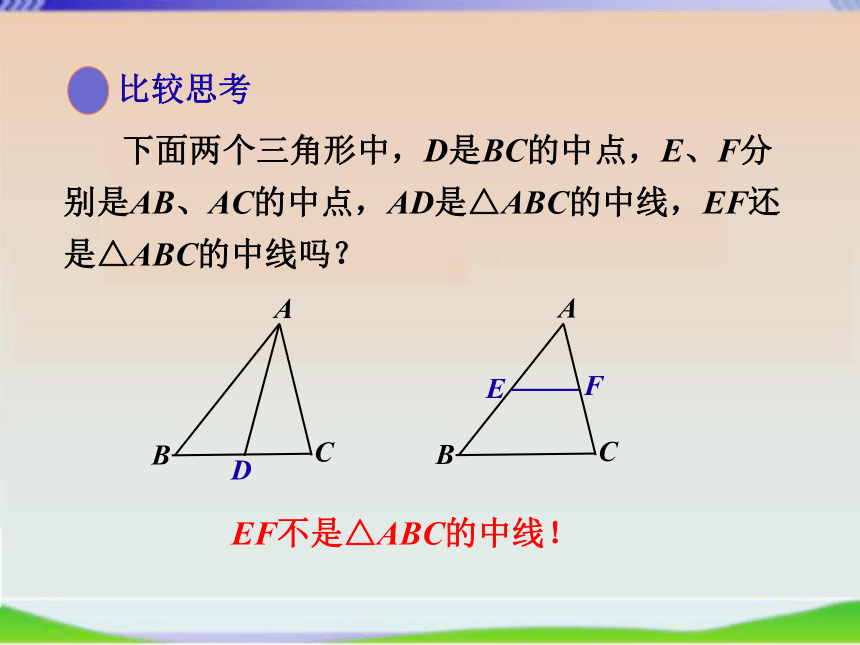
比较思考
A
B
C
D
A
B
C
E
F
下面两个三角形中,D是BC的中点,E、F分别是AB、AC的中点,AD是△ABC的中线,EF还是△ABC的中线吗?
EF不是△ABC的中线!
新概念
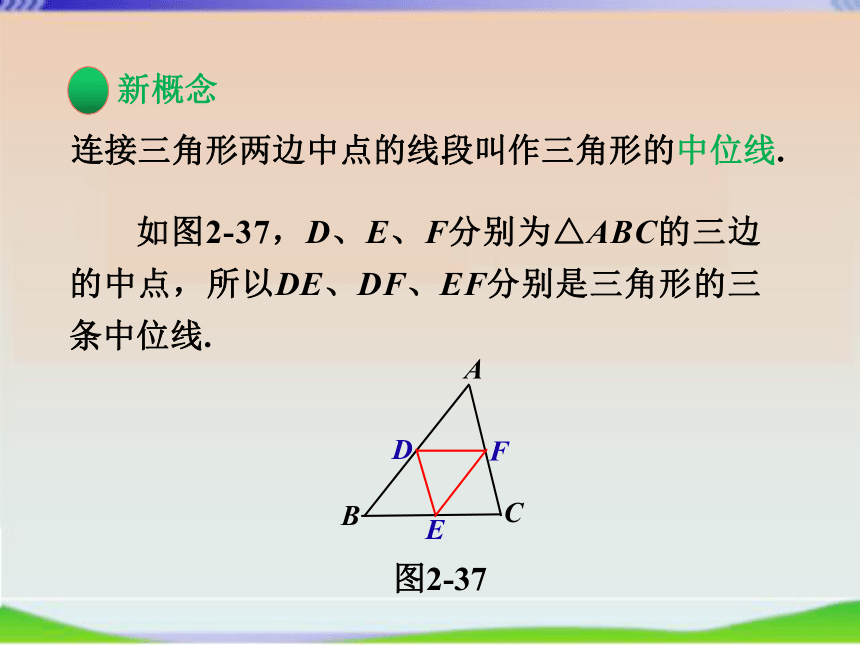
连接三角形两边中点的线段叫作三角形的中位线.
如图2-37,D、E、F分别为△ABC的三边的中点,所以DE、DF、EF分别是三角形的三条中位线.
A
B
C
D
F
E
图2-37
探究
三角形的中位线有哪些性质?
如图2-38,EF是△ABC的一条中位线.
EF∥BC吗?量一量EF与BC的长各是多少?你能猜测EF与BC具有怎样的位置关系和数量关系吗?为什么?
A
B
C
E
F
图2-38
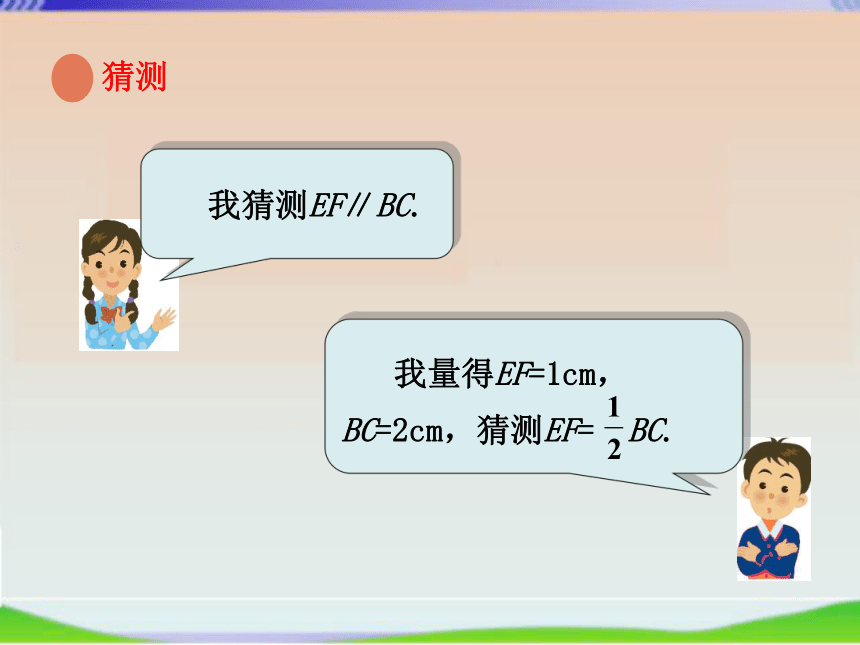
我猜测EF∥BC.
我量得EF=1cm,BC=2cm,猜测EF=
BC.
猜测
证明
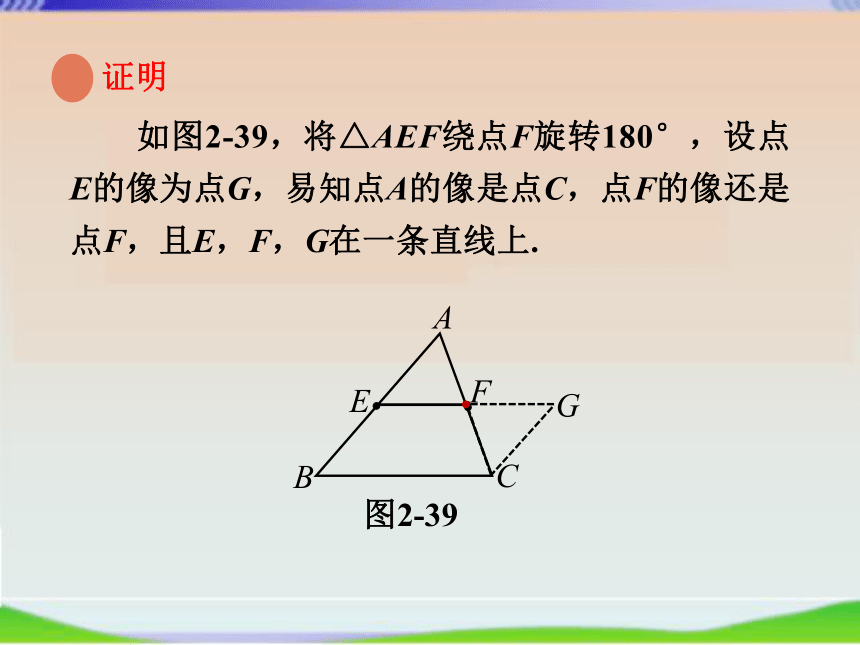
如图2-39,将△AEF绕点F旋转180°,设点E的像为点G,易知点A的像是点C,点F的像还是点F,且E,F,G在一条直线上.
A
B
C
E
F
G
图2-39
A
B
C
E
F
G
由于旋转不改变图形的形状和大小,所以有
CG=AE=BE,GF=EF,∠G=∠AEF.
则
EA∥CG,即
BE∥CG.
∴
四边形BCGF是平行四边形.
∴
EG
BC.
又
∵EF=FG,
∴
EF=
FG=
BC,
从而
EF
BC.
由此得到三角形的中位线定理:
三角形的中位线平行第三边,并且等于第三边的一半.
学
习
例
题
例
如图2-40,顺次连接四边形ABCD各边中点E,F,G,H,得到的四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
解
连接AC.
∵
EF是△ABC的一条中位线,
∴
EF∥AC,且EF=
AC.
又
∵HG是△DAC的一条中位线,
∴
HG∥AC,且HG=
AC.
∴
EF∥HG,且EF=HG.
∴
四边形ABCD是平行四边形.
1.已知△ABC各边的长度分别为3cm,3.4cm,4cm,求连接各边中点所构成的△DEF的周长.
练习
解
∵△DEF
的三边分别是△ABC的三条中位线,
∴△DEF
的周长等于△ABC的周长的一半,
即
(3+3.4+4)÷2=5.2(cm).
2.如图,△ABC的边AB,BC,CA上的中点分别是D,E,F.
(1)四边形ADEF是平行四边形吗?为什么?
(2)四边形ADEF的周长等于AB+AC吗?为什么?
A
B
D
E
C
F
A
B
D
E
C
F
解
(1)∵
DE是△ABC的一条中位线,
∴
DE∥AC,且DE=
AC.
又
∵F是AC的中点,
∴
AF=
AC.
∴
DE=AF,
∴
四边形ADEF是平行四边形.
A
B
D
E
C
F
(2)
由(1)可得,DE+AF=
AC+
AC=AC,
同理,EF+AD=AB,
∴
四边形ADEF的周长等于:
EF+AD+DE+AF=AB+AC.
反
思
总
结
回答问题
1.什么是三角形的中位线?
连接三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线有什么性质?
三角形的中位线平行于第三边,并且等于第三边的一半.
3.我们是怎样证明三角形的中位线定理的?
利用旋转的性质证四边形一组对边平行且相等,用平行四边形的判定定理2判定为平行四边形,再利用平行四边形的性质和已知得出三角形中位线的定理.
4.在例题和练习第2题中,我们用什么哪些依据判定平行四边形?
用三角形的中位线定理和平行四边形的判定定理.
温馨提示
三角形的中位线定理是一个重要的定理.在已知两条线段的中点解决证线段平行和求线段的长度,以及判定特殊四边形等问题中,我们经常会用到这个定理.
三角形的中位线
A
B
C
D
如图,点D是△ABC的边BC的中点,则AD是△ABC的
.
三角形一边上的中线
这一边,并且把三角形的面积分成
的两部分.
看图填空
中位线
平分
相等
复
习
思
考
比较思考
A
B
C
D
A
B
C
E
F
下面两个三角形中,D是BC的中点,E、F分别是AB、AC的中点,AD是△ABC的中线,EF还是△ABC的中线吗?
EF不是△ABC的中线!
新概念
连接三角形两边中点的线段叫作三角形的中位线.
如图2-37,D、E、F分别为△ABC的三边的中点,所以DE、DF、EF分别是三角形的三条中位线.
A
B
C
D
F
E
图2-37
探究
三角形的中位线有哪些性质?
如图2-38,EF是△ABC的一条中位线.
EF∥BC吗?量一量EF与BC的长各是多少?你能猜测EF与BC具有怎样的位置关系和数量关系吗?为什么?
A
B
C
E
F
图2-38
我猜测EF∥BC.
我量得EF=1cm,BC=2cm,猜测EF=
BC.
猜测
证明
如图2-39,将△AEF绕点F旋转180°,设点E的像为点G,易知点A的像是点C,点F的像还是点F,且E,F,G在一条直线上.
A
B
C
E
F
G
图2-39
A
B
C
E
F
G
由于旋转不改变图形的形状和大小,所以有
CG=AE=BE,GF=EF,∠G=∠AEF.
则
EA∥CG,即
BE∥CG.
∴
四边形BCGF是平行四边形.
∴
EG
BC.
又
∵EF=FG,
∴
EF=
FG=
BC,
从而
EF
BC.
由此得到三角形的中位线定理:
三角形的中位线平行第三边,并且等于第三边的一半.
学
习
例
题
例
如图2-40,顺次连接四边形ABCD各边中点E,F,G,H,得到的四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
解
连接AC.
∵
EF是△ABC的一条中位线,
∴
EF∥AC,且EF=
AC.
又
∵HG是△DAC的一条中位线,
∴
HG∥AC,且HG=
AC.
∴
EF∥HG,且EF=HG.
∴
四边形ABCD是平行四边形.
1.已知△ABC各边的长度分别为3cm,3.4cm,4cm,求连接各边中点所构成的△DEF的周长.
练习
解
∵△DEF
的三边分别是△ABC的三条中位线,
∴△DEF
的周长等于△ABC的周长的一半,
即
(3+3.4+4)÷2=5.2(cm).
2.如图,△ABC的边AB,BC,CA上的中点分别是D,E,F.
(1)四边形ADEF是平行四边形吗?为什么?
(2)四边形ADEF的周长等于AB+AC吗?为什么?
A
B
D
E
C
F
A
B
D
E
C
F
解
(1)∵
DE是△ABC的一条中位线,
∴
DE∥AC,且DE=
AC.
又
∵F是AC的中点,
∴
AF=
AC.
∴
DE=AF,
∴
四边形ADEF是平行四边形.
A
B
D
E
C
F
(2)
由(1)可得,DE+AF=
AC+
AC=AC,
同理,EF+AD=AB,
∴
四边形ADEF的周长等于:
EF+AD+DE+AF=AB+AC.
反
思
总
结
回答问题
1.什么是三角形的中位线?
连接三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线有什么性质?
三角形的中位线平行于第三边,并且等于第三边的一半.
3.我们是怎样证明三角形的中位线定理的?
利用旋转的性质证四边形一组对边平行且相等,用平行四边形的判定定理2判定为平行四边形,再利用平行四边形的性质和已知得出三角形中位线的定理.
4.在例题和练习第2题中,我们用什么哪些依据判定平行四边形?
用三角形的中位线定理和平行四边形的判定定理.
温馨提示
三角形的中位线定理是一个重要的定理.在已知两条线段的中点解决证线段平行和求线段的长度,以及判定特殊四边形等问题中,我们经常会用到这个定理.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
