湘教版八年级数学下册2.5.1矩形的性质课件(22张)
文档属性
| 名称 | 湘教版八年级数学下册2.5.1矩形的性质课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
矩形的性质
复
习
O
A
B
C
D
平行四边形的性质:
①对边平行且相等——边的性质
②对角相等,邻角互补——角的性质
③对角线互相平分——对角线的性质
④平行四边形是中心对称图形,对角线的交点是它的对称中心——对称性
在小学,我们初步认识了长方形,观察图2-41中的长方形,它是什么平行四边形吗?它有什么特点呢?
图2-41
这些四边形的四个角都是直角.
在一个平行四边形中,
只要有一个角是直角,那
么其他三个角都是直角.
我发现这些长方形的对边平行且相等,因此,它们是平行四边形.
有一个角是直角的平行四边形叫做矩形,也称为长方形.
矩
形
有一个角是直角
平行四边形
矩形的四个角都是直角,对边相等,对角线互相平分.
可以知道:
矩形是中心对称图形,对角线的交点是它的对称中心.
由于矩形是平行四边形,因此
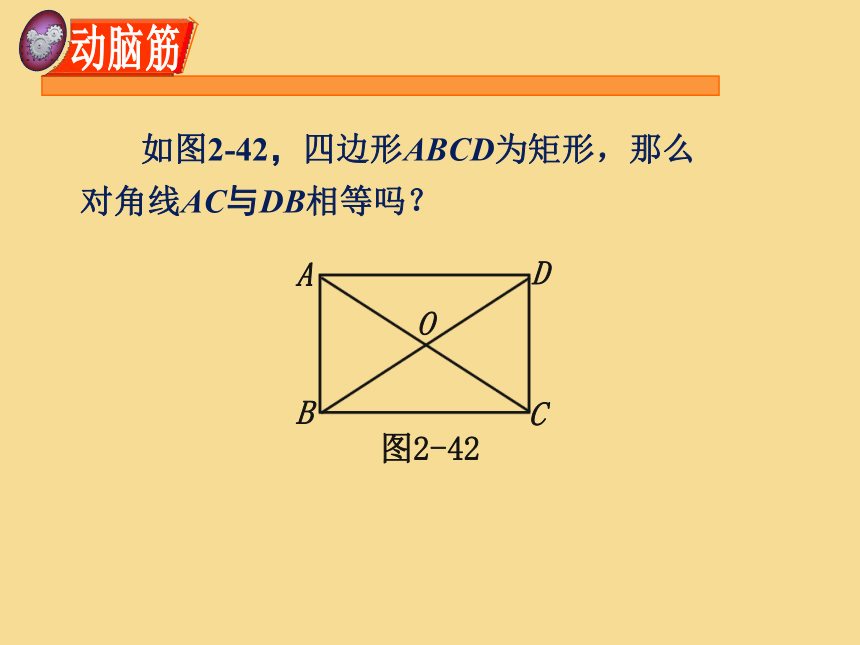
如图2-42,四边形ABCD为矩形,那么对角线AC与DB相等吗?
图2-42
A
B
C
D
O
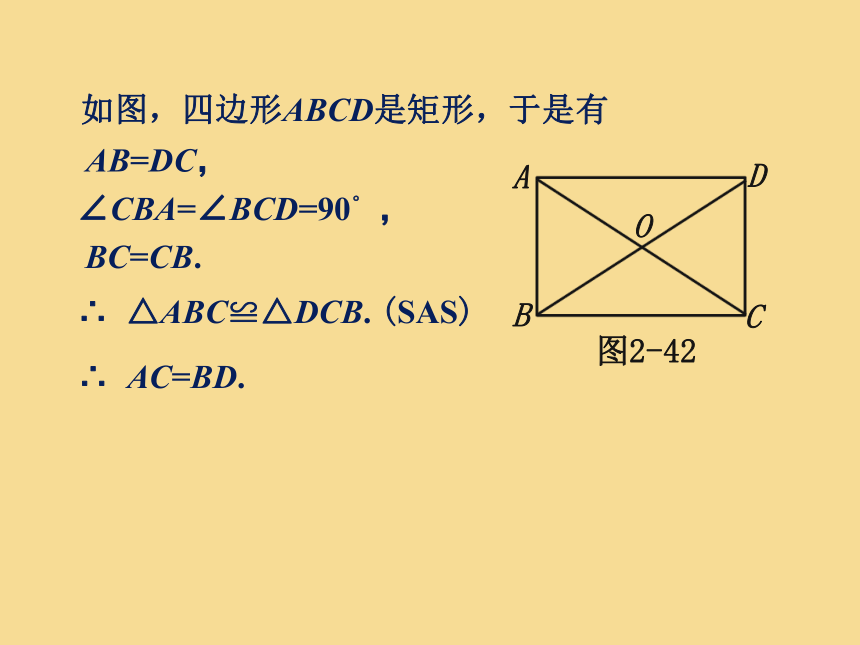
如图,四边形ABCD是矩形,于是有
AB=DC,
∠CBA=∠BCD=90°
,
BC=CB.
∴
△ABC≌△DCB.
(SAS)
∴
AC=BD.
图2-42
A
B
C
D
O
矩形的对角线相等.
由此得到矩形的性质:
如图2-43,矩形ABCD的两条对角线AC
,BD相交于点O,AC
=
4
cm,
∠AOB
=
60°.
求BC的长.
例1
图2-43
A
B
C
D
O
∴
△AOB是等边三角形.
∴
AB=OA=2cm.
又∠AOB
=
60°,
∵
∠ABC
=
90°,
∴
在Rt△ABC中,
解
∵
□ABCD是矩形,
从而
图2-43
A
B
C
D
O
在纸上画一个矩形ABCD(如图2-44),把它剪下来,怎样折叠能使矩形在折痕两旁的部分互相重合?满足这个要求的折叠方法有几种?由此猜测:矩形是轴对称图形吗?如果是,它有几条对称轴?你的猜测正确吗?
图2-44
A
B
C
D
如图,矩形ABCD的对角线相交于点O.
B
C
D
A
O
F
E
过点O作直线EF⊥BC,且分别与边BC
,AD相交于点E,F.
由于
,
因此△OBC是等腰三角形,从而直线EF是线段BC的垂直平分线.
由于AD∥BC,因此EF⊥AD.
同理,直线EF是线段AD的垂直平分线.
因此点B和点C关于直线EF对称,点A和点D关于直线EF对称,从而在关于直线EF的轴反射下,矩形ABCD的像与它自身重合,因此矩形ABCD是轴对称图形,直线EF是矩形ABCD的一条对称轴.
B
C
D
A
O
F
E
类似地,过点O作直线MN⊥AB,且分别与边AB,DC相交于点M,N,则点M,N分别是边AB,DC的中点,直线MN是矩形ABCD的一条对称轴.
B
C
D
A
O
F
E
M
N
矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.
由此得到:
1.已知矩形的一条对角线的长度为2cm,两条对角线的一个夹角为60°,求矩形的各边长.
练习
提示:矩形的对角线把矩形分成两对全等的等腰三角形和四个全等的直角三角形.把矩形问题转化为三角形的问题求解.
A
B
C
D
O
解
根据题意画出矩形如图,AC=2cm,∠AOB=60°.
1
2
∵四边形ABCD是矩形,
∴OA=OB=
AC=1cm,
∴△AOB为等边三角形.
∴AB=OA=1cm.
在Rt△ABC中,根据勾股定理,得
BC?=AC?-AB?=2?-1?=3,
∴BC=
(cm)
2.
如图,四边形ABCD
为矩形,试利用矩形的性质说明:直角三角形ABC斜边AC上的中线BO等于斜边的一半.
证明
∵
四边形ABCD是矩形,
(矩形的对角线互相平分)
又
AC=BD(
),
OB=OA=OC
∴
,
.
矩形的对角线相等
∴
.。
A
B
C
D
O
OA=OC=
AC
OB=OD=
BD
1
2
1
2
反思总结:
矩形是特殊的平行四边形,什么叫做矩形?
有一个角是直角的平行四边形叫做矩形.
平行四边形
有一个角是直角
矩形
矩形除具有平行四边形的性质外,还具有哪些性质?
①矩形的四个角都是直角.
②矩形的对角线相等,因此矩形的对角线把矩形分成两对全等的等腰三角形和四个全等的直角三角形.
③矩形既是中心对称图形也是轴对称图形.
A
B
C
D
O
B
C
D
A
O
F
E
M
N
矩形的性质
复
习
O
A
B
C
D
平行四边形的性质:
①对边平行且相等——边的性质
②对角相等,邻角互补——角的性质
③对角线互相平分——对角线的性质
④平行四边形是中心对称图形,对角线的交点是它的对称中心——对称性
在小学,我们初步认识了长方形,观察图2-41中的长方形,它是什么平行四边形吗?它有什么特点呢?
图2-41
这些四边形的四个角都是直角.
在一个平行四边形中,
只要有一个角是直角,那
么其他三个角都是直角.
我发现这些长方形的对边平行且相等,因此,它们是平行四边形.
有一个角是直角的平行四边形叫做矩形,也称为长方形.
矩
形
有一个角是直角
平行四边形
矩形的四个角都是直角,对边相等,对角线互相平分.
可以知道:
矩形是中心对称图形,对角线的交点是它的对称中心.
由于矩形是平行四边形,因此
如图2-42,四边形ABCD为矩形,那么对角线AC与DB相等吗?
图2-42
A
B
C
D
O
如图,四边形ABCD是矩形,于是有
AB=DC,
∠CBA=∠BCD=90°
,
BC=CB.
∴
△ABC≌△DCB.
(SAS)
∴
AC=BD.
图2-42
A
B
C
D
O
矩形的对角线相等.
由此得到矩形的性质:
如图2-43,矩形ABCD的两条对角线AC
,BD相交于点O,AC
=
4
cm,
∠AOB
=
60°.
求BC的长.
例1
图2-43
A
B
C
D
O
∴
△AOB是等边三角形.
∴
AB=OA=2cm.
又∠AOB
=
60°,
∵
∠ABC
=
90°,
∴
在Rt△ABC中,
解
∵
□ABCD是矩形,
从而
图2-43
A
B
C
D
O
在纸上画一个矩形ABCD(如图2-44),把它剪下来,怎样折叠能使矩形在折痕两旁的部分互相重合?满足这个要求的折叠方法有几种?由此猜测:矩形是轴对称图形吗?如果是,它有几条对称轴?你的猜测正确吗?
图2-44
A
B
C
D
如图,矩形ABCD的对角线相交于点O.
B
C
D
A
O
F
E
过点O作直线EF⊥BC,且分别与边BC
,AD相交于点E,F.
由于
,
因此△OBC是等腰三角形,从而直线EF是线段BC的垂直平分线.
由于AD∥BC,因此EF⊥AD.
同理,直线EF是线段AD的垂直平分线.
因此点B和点C关于直线EF对称,点A和点D关于直线EF对称,从而在关于直线EF的轴反射下,矩形ABCD的像与它自身重合,因此矩形ABCD是轴对称图形,直线EF是矩形ABCD的一条对称轴.
B
C
D
A
O
F
E
类似地,过点O作直线MN⊥AB,且分别与边AB,DC相交于点M,N,则点M,N分别是边AB,DC的中点,直线MN是矩形ABCD的一条对称轴.
B
C
D
A
O
F
E
M
N
矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.
由此得到:
1.已知矩形的一条对角线的长度为2cm,两条对角线的一个夹角为60°,求矩形的各边长.
练习
提示:矩形的对角线把矩形分成两对全等的等腰三角形和四个全等的直角三角形.把矩形问题转化为三角形的问题求解.
A
B
C
D
O
解
根据题意画出矩形如图,AC=2cm,∠AOB=60°.
1
2
∵四边形ABCD是矩形,
∴OA=OB=
AC=1cm,
∴△AOB为等边三角形.
∴AB=OA=1cm.
在Rt△ABC中,根据勾股定理,得
BC?=AC?-AB?=2?-1?=3,
∴BC=
(cm)
2.
如图,四边形ABCD
为矩形,试利用矩形的性质说明:直角三角形ABC斜边AC上的中线BO等于斜边的一半.
证明
∵
四边形ABCD是矩形,
(矩形的对角线互相平分)
又
AC=BD(
),
OB=OA=OC
∴
,
.
矩形的对角线相等
∴
.。
A
B
C
D
O
OA=OC=
AC
OB=OD=
BD
1
2
1
2
反思总结:
矩形是特殊的平行四边形,什么叫做矩形?
有一个角是直角的平行四边形叫做矩形.
平行四边形
有一个角是直角
矩形
矩形除具有平行四边形的性质外,还具有哪些性质?
①矩形的四个角都是直角.
②矩形的对角线相等,因此矩形的对角线把矩形分成两对全等的等腰三角形和四个全等的直角三角形.
③矩形既是中心对称图形也是轴对称图形.
A
B
C
D
O
B
C
D
A
O
F
E
M
N
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
