湘教版八年级数学下册2.5.2矩形的判定课件(20张PPT)
文档属性
| 名称 | 湘教版八年级数学下册2.5.2矩形的判定课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
矩形的判定
两组对边
分别平行
一个角
是直角
四边形
平行四边形
矩形
复
习
思
考
看图说定义
1
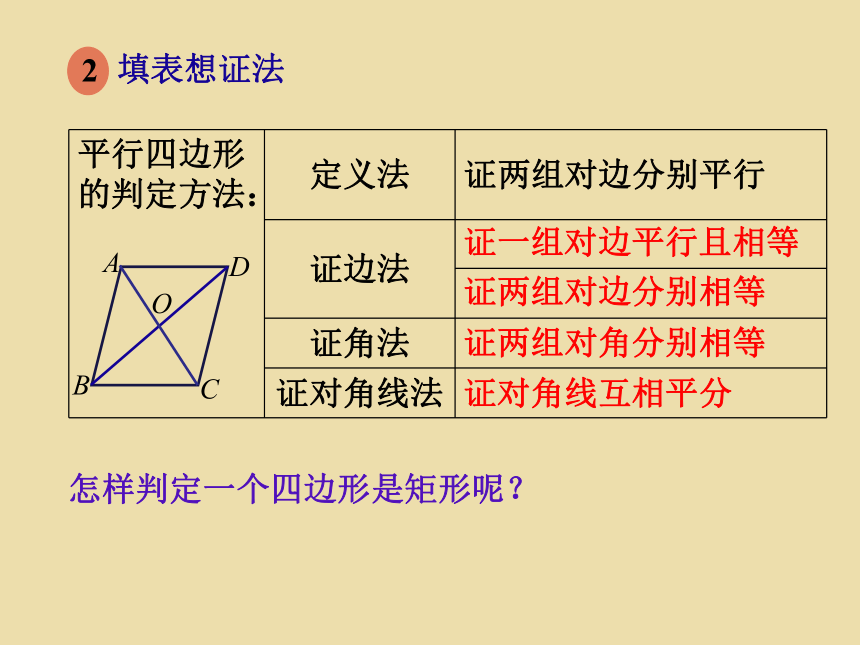
填表想证法
2
平行四边形的判定方法:
定义法
证两组对边分别平行
证边法
证角法
证对角线法
O
A
B
C
D
证一组对边平行且相等
证两组对边分别相等
证两组对角分别相等
证对角线互相平分
怎样判定一个四边形是矩形呢?
矩形的四个角是直角,那么,四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?
A
B
C
D
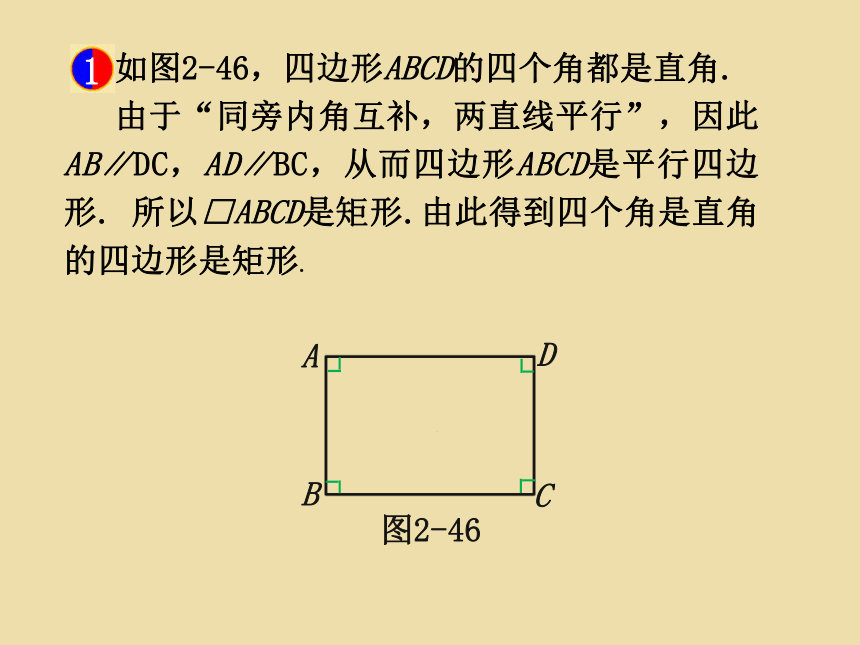
探究(一)
如图2-46,四边形ABCD的四个角都是直角.
由于“同旁内角互补,两直线平行”,因此AB∥DC,AD∥BC,从而四边形ABCD是平行四边形.
所以□ABCD是矩形.由此得到四个角是直角的四边形是矩形.
1
图2-46
A
B
C
D
三个角是直角的四边形是矩形.
三个角是直角的四边形,根据四边形的内角和等于360°,容易知道另一个角也是直角,由此得到:
2
这两个四边形两个角是直角,但都不是矩形.所以,必须有三个角是直角的四边形才是矩形.
两个角是直角的四边形,根据四边形的内角和等于360°,则另外两个角的和为180°,这样的四边形中你能想到不是矩形的吗?
3
探究(二)
从“矩形的两条对角线相等且互相平分”这一性质受到启发,你能画出画出一个长度为4cm的矩形吗?这样的矩形有多少个?
1
对于是不是矩形,我们可以这样做:
①画图:过点O画两条线段AC,BD,使得OA=OC=2cm,OB=OD=2cm.
连接AB,BC,CD,DA.
图2-47
A
B
C
D
O
②量一量:量所画的四边形ABCD是否有三个角为直角(可用三角尺的直角比一比).
你能说出这样画出的四边形一定是矩形的道理吗?
2
图2-47
A
B
C
D
O
如图2-47,由画法可知,四边形ABCD的两条对角线互相平分,因此它是平行四边形,又已知其对角线相等.上述问题抽象出来就是:对角线相等的平行四边形是矩形吗?
△ABC≌△DCB(SSS)
∴
∠ABC=∠DCB.
∵
AB∥CD,
∴
.
∠ABC
+∠DCB=180°,
∴
∠ABC=
.
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
在□ABCD中,∵AB=DC,BC=CB,AC=DB,
∴
.
下面我们来证明:
90°
A
B
C
D
O
由此得到:
对角线相等的平行四边形是矩形.
3
这样的矩形可以画多少个?
可以这样想:把对角线绕点O旋转到不同的位置,就能得到形状不同的矩形,因此,这样的矩形有无数个.
O
对角线相等的四边形是矩形吗?
等腰梯形的对角线也相等,因此对角线相等
的四边形不一定是矩形.
如图2-48,在□ABCD中,它的两条对角线相
交于点O.
(1)如果□ABCD是矩形,试问:△OBC是什么样
的三角形?
(2)如果△OBC是等腰三角形,其中OB=OC,那么
□ABCD是矩形吗?
图2-48
A
B
C
D
O
例2
(2)
∵
△OBC是等腰三角形,其中OB
=
OC,
解
(1)
∵□ABCD是矩形,
∴
AC与DB相等且互相平分.
∴
△OBC是等腰三角形.
∴
AC
=
2OC
=
2OB
=
BD.
∴
□ABCD是矩形.
图2-48
A
B
C
D
O
∴
1.
如图,在四边形ABCD中,
∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.
A
B
C
D
练习
证明:∵∠A=∠B=∠C=∠D
,∠A+∠B+∠C+∠D
=360°,
∴∠A=∠B=∠C=∠D=
90°
.
∴四边形ABCD是矩形.
(三个角是直角的四边形是矩形.)
2.
如图,在□ABCD中,对角线AC,BD相交于点O,∠AOB
=60°,AB=2,AC=4,求□ABCD的面积.
解
∵
OA=
=2,AB=
2,
∴
△OAB是等腰三角形.
∴
△OAB是等边三角形.
又∠AOB
=
60°,
∴
OA=OB=2,
∴
AC=BD=4.
∴□ABCD是矩形.
A
B
C
D
O
在Rt△ABC中,AB=2,AC=4,
根据勾股定理,得
BC?=AC?-AB?=4?-2?=12
∴
BC=
.
∴
矩形的面积S=AB·BC=
.
A
B
C
D
O
反
思
总
结
四边形
+
三个角是直角
对角线互相平分且相等
+
一个角是直角
平行四边形
对角线相等
矩形
矩形的判定
两组对边
分别平行
一个角
是直角
四边形
平行四边形
矩形
复
习
思
考
看图说定义
1
填表想证法
2
平行四边形的判定方法:
定义法
证两组对边分别平行
证边法
证角法
证对角线法
O
A
B
C
D
证一组对边平行且相等
证两组对边分别相等
证两组对角分别相等
证对角线互相平分
怎样判定一个四边形是矩形呢?
矩形的四个角是直角,那么,四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?
A
B
C
D
探究(一)
如图2-46,四边形ABCD的四个角都是直角.
由于“同旁内角互补,两直线平行”,因此AB∥DC,AD∥BC,从而四边形ABCD是平行四边形.
所以□ABCD是矩形.由此得到四个角是直角的四边形是矩形.
1
图2-46
A
B
C
D
三个角是直角的四边形是矩形.
三个角是直角的四边形,根据四边形的内角和等于360°,容易知道另一个角也是直角,由此得到:
2
这两个四边形两个角是直角,但都不是矩形.所以,必须有三个角是直角的四边形才是矩形.
两个角是直角的四边形,根据四边形的内角和等于360°,则另外两个角的和为180°,这样的四边形中你能想到不是矩形的吗?
3
探究(二)
从“矩形的两条对角线相等且互相平分”这一性质受到启发,你能画出画出一个长度为4cm的矩形吗?这样的矩形有多少个?
1
对于是不是矩形,我们可以这样做:
①画图:过点O画两条线段AC,BD,使得OA=OC=2cm,OB=OD=2cm.
连接AB,BC,CD,DA.
图2-47
A
B
C
D
O
②量一量:量所画的四边形ABCD是否有三个角为直角(可用三角尺的直角比一比).
你能说出这样画出的四边形一定是矩形的道理吗?
2
图2-47
A
B
C
D
O
如图2-47,由画法可知,四边形ABCD的两条对角线互相平分,因此它是平行四边形,又已知其对角线相等.上述问题抽象出来就是:对角线相等的平行四边形是矩形吗?
△ABC≌△DCB(SSS)
∴
∠ABC=∠DCB.
∵
AB∥CD,
∴
.
∠ABC
+∠DCB=180°,
∴
∠ABC=
.
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
在□ABCD中,∵AB=DC,BC=CB,AC=DB,
∴
.
下面我们来证明:
90°
A
B
C
D
O
由此得到:
对角线相等的平行四边形是矩形.
3
这样的矩形可以画多少个?
可以这样想:把对角线绕点O旋转到不同的位置,就能得到形状不同的矩形,因此,这样的矩形有无数个.
O
对角线相等的四边形是矩形吗?
等腰梯形的对角线也相等,因此对角线相等
的四边形不一定是矩形.
如图2-48,在□ABCD中,它的两条对角线相
交于点O.
(1)如果□ABCD是矩形,试问:△OBC是什么样
的三角形?
(2)如果△OBC是等腰三角形,其中OB=OC,那么
□ABCD是矩形吗?
图2-48
A
B
C
D
O
例2
(2)
∵
△OBC是等腰三角形,其中OB
=
OC,
解
(1)
∵□ABCD是矩形,
∴
AC与DB相等且互相平分.
∴
△OBC是等腰三角形.
∴
AC
=
2OC
=
2OB
=
BD.
∴
□ABCD是矩形.
图2-48
A
B
C
D
O
∴
1.
如图,在四边形ABCD中,
∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.
A
B
C
D
练习
证明:∵∠A=∠B=∠C=∠D
,∠A+∠B+∠C+∠D
=360°,
∴∠A=∠B=∠C=∠D=
90°
.
∴四边形ABCD是矩形.
(三个角是直角的四边形是矩形.)
2.
如图,在□ABCD中,对角线AC,BD相交于点O,∠AOB
=60°,AB=2,AC=4,求□ABCD的面积.
解
∵
OA=
=2,AB=
2,
∴
△OAB是等腰三角形.
∴
△OAB是等边三角形.
又∠AOB
=
60°,
∴
OA=OB=2,
∴
AC=BD=4.
∴□ABCD是矩形.
A
B
C
D
O
在Rt△ABC中,AB=2,AC=4,
根据勾股定理,得
BC?=AC?-AB?=4?-2?=12
∴
BC=
.
∴
矩形的面积S=AB·BC=
.
A
B
C
D
O
反
思
总
结
四边形
+
三个角是直角
对角线互相平分且相等
+
一个角是直角
平行四边形
对角线相等
矩形
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
