17.3 一次函数 同步练习(含解析)
文档属性
| 名称 | 17.3 一次函数 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 14:58:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第17章 17.3 一次函数
一、单选题
1.下列函数关系式: , , , , 其中是一次函数的是(?? ) 21教育网
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
2.一次函数 的图象经过(?? )
A.?第一、二、三象限?????????B.?第一、三、四象限?????????C.?第二、三、四象限?????????D.?第一、二、四象限
3.若一个正比例函数的图象经过点(2,﹣3),则这个图象一定也经过点(?? )
A.?( ,﹣1)???????????????????B.?( ,﹣1)???????????????????C.?(﹣3,2)???????????????????D.?(﹣ ,1)
4.已知正比例函数 的图像上有两点且 , ,且x1>x2 , 则y1与y2的大小关系是( ) 【来源:21·世纪·教育·网】
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?不能确定.
5.直线 向上平移 个单位得到的直线解析式是(? )
A.?.??????????????????????B.???????????????????????C.???????????????????????D.?
6.若一次函数y=(m-3)x_-4??????è±????_过点A(x1 , y1 )和点B(x2 , y2),当x1y2 , 则m的取值范围是(?? ) 【来源:21cnj*y.co*m】
A.?m<3????????????????????????????????????B.?m>3????????????????????????????????????C.?m≤3????????????????????????????????????D.?m≥3
二、填空题
7.登山队大本_è???????¨??°?°????_为5℃,海拔每升高1 km气温下降6℃。登山队员由大本营向上登高xkm时,所在位置的气温为y℃。则y与x的函数关系式是________。
8.若一个正比例函数的图象经过 、 )两点,则 的值为________.
9.已知点P1(a,7),P2(a + 1,9)在直线y = kx + 7上,则k =? ________ .
10.已知一次函数 的图象经过 , 两点,则 ________ (填“>”,“<”或“=”).
三、综合题
11.若△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,试写出y与x之间的函数关系式,并画出图象.
12.现从A,B两个水果市_?????????????????¤_地运送水果,A,B两个水果市场各有水果20 t,其中甲地需要水果22 t,乙地需要水果18 t,从A水果市场到甲地运费为50元/t,到乙地为30元/t;从B水果市场到甲地运费为60元/t,到乙地为45元/t.
(1)设A水果市场运送x(t)水果到甲地,请完成下表:
运往甲地(单位︰吨) 运往乙地(单位:吨)
A x
B
(2)设总运费为y元,请写出y关于x的函数表达式,求出自变量x的取值范围,并在平面直角坐标系中画出此函数的图象. 【出处:21教育名师】
(3)当A,B两个水果市场向甲、乙两地运送水果各多少吨时,总运费最少?最少是多少?
13.如图1,直线AB:y= x+4分别与x轴、y轴交于A、B两点,过点B的直线交x轴负半轴于点C , 将△BOC沿BC折叠,使点O落在BA上的点M处.
(1)求A、B两点的坐标;
(2)求线段BC的长;
(3)点P为x轴上的动点,当∠PBA=45°时,求点P的坐标.
14.如图,已知过点B(1,0)的直线 与直线 :y=2x+4相交于点P(-1,a).
(1)(1)求直线 的解析式;
(2)(2)求四边形PAOC的面积.
15.如图,l1表示某商场一天的手提电脑销售额与销售量的关系,l2表示该商场一天的销售成本与手提电脑销售量的关系.
(1)当销售量x=2时,销售额=________万元,销售成本=________万元,利润(收入-成本)________=万元.
(2)一天销售________台时,销售额等于销售成本.
(3)当销售量________时,该商场赢利(收入大于成本),当销售量________时,该商场亏损(收入小于成本).
(4)l1对应的函数表达式是________.
(5)写出利润与销售额之间的函数表达式________.
答案解析部分
一、单选题
1.【答案】 A
解: 是一次函数;
自变量次数不为1,故不是一次函数;
自变量次数不为1,故不是一次函数;
是常数;
是一次函数.
所以一次函数是 .
故答案为:A.
2.【答案】 D
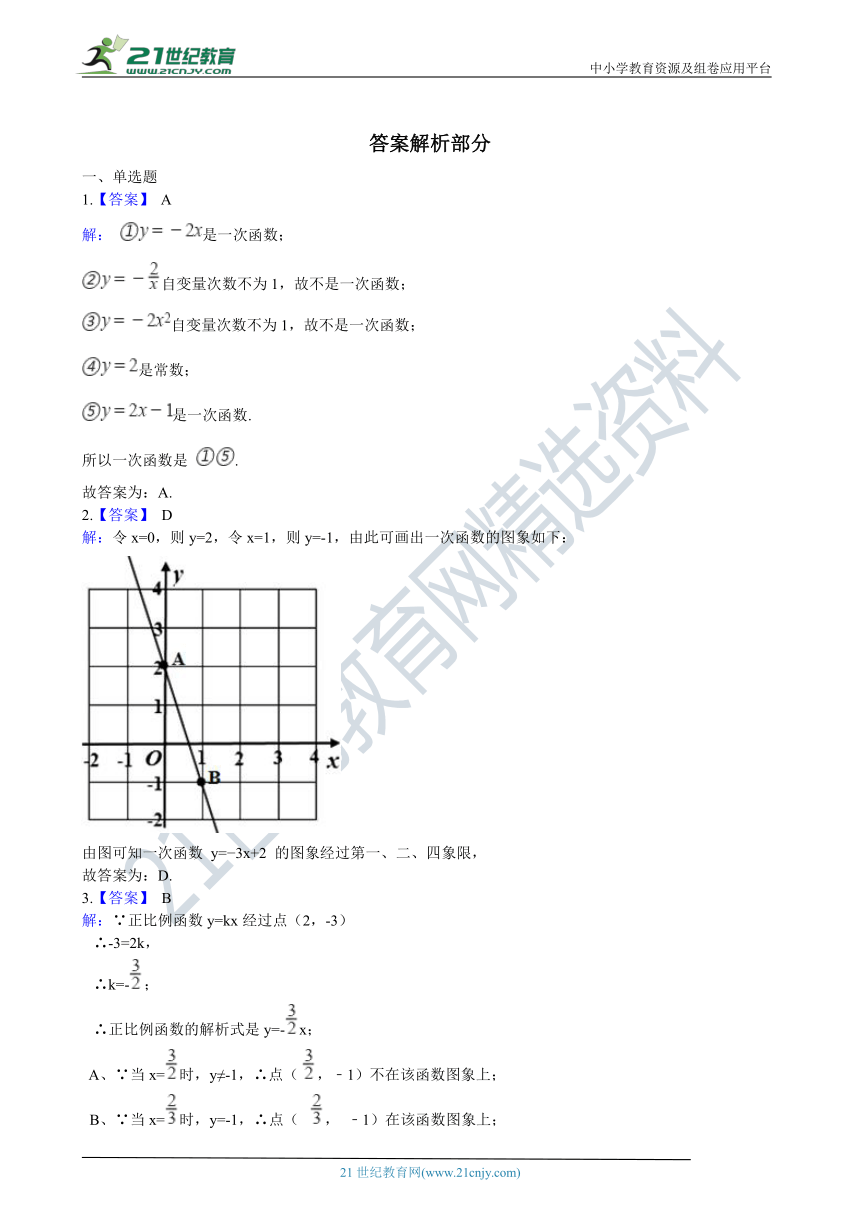
解:令x=0,则y=2,令x=1,则y=-1,由此可画出一次函数的图象如下:
由图可知一次函数 y=?3x+2 的图象经过第一、二、四象限,
故答案为:D.
3.【答案】 B
解:∵正比例函数y=kx经过点(2,-3)
?∴-3=2k,
?∴k=-;
?∴正比例函数的解析式是y=-x;
A、∵当x=时,y≠-1,∴点(?,﹣1)不在该函数图象上;
B、∵当x=时,y=-1,∴点(? , ﹣1)在该函数图象上;
C、∵当x=-3时, y≠2,∴点(-3? ,2)不在该函数图象上;
D、∵当x=-时, y≠1,∴点(-? ,1)不在该函数图象上.
故答案为:B
4.【答案】 B
解:∵正比例函数y=kx中,k>0,
∴此函数是增函数.
∵x1>x2 ,
∴y1>y2 .
故答案为:B.
5.【答案】 A
解:直线 向上平移 个单位得到的直线解析式是 .
故答案为:A.
6.【答案】 A
解:由_é??????????????m_-3<0,
解得m<3.
故答案为:A.
二、填空题
7.【答案】 y=5-6x
解: _??±é????????y???_x之间的函数关系式为:y=5-6x.
故答案为:y=5-6x.
8.【答案】 4
解:设正比例函数为y=kx,
将点 代入得:4k=8,解得:k=2,
∴y=2x,
将点 代入得:2m=8,解得m=4,
故答案为:4.
9.【答案】 2
解:将P1(a,7),P2(a+1,9)代入y=kx+7中,得
②-①,得k=2.
故答案为:2.
10.【答案】 <
解:由一次函数 可得:k=3>0,
∴y随x的增大而增大,
∵函数图像经过 , 两点,
∴ ,
故答案为<.
三、综合题
11.【答案】 解:∵△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,
∴y=180°-60°-x,整理得:
y=120°-x( ),
将y=0和x=0两个值代入解析式,得到图像与坐标轴的两个交点坐标分别为(0,120),(120,0)画出图像如下:2-1-c-n-j-y
12.【答案】 (1)解:A地运_????????°???é?????_20-x,B地运往甲地的量为22-x,B地运往乙地的量为20-(22-x)=x-2,
如下所示: 21教育名师原创作品
? 运往甲地(单位︰吨) 运往乙地(单位:吨)
A x 20-x
B 22-x x-2
(2)解:y=50x+30(20-x)+60(22-x)+45(x-2)=5x+1830.
∵A、B到两地运送的水果量为非负数,
∴x≥0,20-x≥0,22-x≥0,x-2≥0,
∴2≤x≤20,
∴ 函数表达式为y=5x+1830(2≤x≤20).
函数图像如下所示:
(3)解:∵y=5x+1830(2≤x≤20)中,y随x的增大而增大,
∴当x=2时,总运费最少,
∴当A水果市场向甲、乙两地各运送2吨、18吨,B水果市场向甲、乙两地各运送20吨、0吨时,总运费最少,最少为1840元. 21世纪教育网版权所有
13.【答案】 (1)解: y=x+4,当x=0时,y=4,当y=0时,x=-3,
∴ A(-3,0),B(0,4) ;
(2)解: 由折叠得,CM=CO,∠CMB=∠BOC=90°,BM=OB=4,
∴AC=OA-OC=3-OC,
在Rt△AOB中,OA=3,OB=4,∴AB=5,
∴AM=AB-BM=1,
在Rt△AMC中,CM2+AM2=AC2 , 即OC2+12=(3-OC)2 ,
解得OC=,
∴BC==;
(3)解: 设P(m,0),∴PB=,
点P到AB的距离为d==,
∵∠PBA=45°,∴BP=, 即得=×,
解得m=-28或m=,
∴ P(-28,0)或(??,0) .
14.【答案】 (1)解:∵点p(-1,a)在直线l2:y=2x+4上,
? ∴2×(-1)+4=a? 解得a=2
? 则P的坐标为(-1,2),
设直线l1的解析式为:y=kx+b(k≠0),那么
? 解得:
?∴l1的解析式为:y=-x+1
(2)解:∵直线l1与y轴相交于点C,
∴C的坐标为(0,1),
又 直线l2与x轴相交于点A,
?∴A点的坐标为(-2,0),则AB=3
? 而
∴
15.【答案】 (1)2;3;-1
(2)4
(3)大于4;小于4
(4)y=x
(5)
解:(1)如图,∵ 过点(0,0),(4,4),
∴设l1的解析式为y=kx,
∴k=1,
∴直线 为:y=x,
∵ 过点(0,2),(4,4),
∴直线 为:y= x+2,
把x=2代入 :y=2,
把x=2代入 :y= 2+2=3,
∴销售额=2,销售成本=3,利润=-1
故答案为:2;3;-1
( 2 )如图可得x=4,
故答案为:4;
( 3 )如图可得,x 4时,该商场赢利,当x 4时,该商场亏损.
故答案为:大于4,小于4
( 4 )由(1)可知:y=x
( 5 )设销售x台时的利润为y万元,则:
当x=2时,y=2-3=-1当x=4时,y=4-4=0
所以 ,解得 ,
∴
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第17章 17.3 一次函数
一、单选题
1.下列函数关系式: , , , , 其中是一次函数的是(?? ) 21教育网
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
2.一次函数 的图象经过(?? )
A.?第一、二、三象限?????????B.?第一、三、四象限?????????C.?第二、三、四象限?????????D.?第一、二、四象限
3.若一个正比例函数的图象经过点(2,﹣3),则这个图象一定也经过点(?? )
A.?( ,﹣1)???????????????????B.?( ,﹣1)???????????????????C.?(﹣3,2)???????????????????D.?(﹣ ,1)
4.已知正比例函数 的图像上有两点且 , ,且x1>x2 , 则y1与y2的大小关系是( ) 【来源:21·世纪·教育·网】
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?不能确定.
5.直线 向上平移 个单位得到的直线解析式是(? )
A.?.??????????????????????B.???????????????????????C.???????????????????????D.?
6.若一次函数y=(m-3)x_-4??????è±????_过点A(x1 , y1 )和点B(x2 , y2),当x1
A.?m<3????????????????????????????????????B.?m>3????????????????????????????????????C.?m≤3????????????????????????????????????D.?m≥3
二、填空题
7.登山队大本_è???????¨??°?°????_为5℃,海拔每升高1 km气温下降6℃。登山队员由大本营向上登高xkm时,所在位置的气温为y℃。则y与x的函数关系式是________。
8.若一个正比例函数的图象经过 、 )两点,则 的值为________.
9.已知点P1(a,7),P2(a + 1,9)在直线y = kx + 7上,则k =? ________ .
10.已知一次函数 的图象经过 , 两点,则 ________ (填“>”,“<”或“=”).
三、综合题
11.若△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,试写出y与x之间的函数关系式,并画出图象.
12.现从A,B两个水果市_?????????????????¤_地运送水果,A,B两个水果市场各有水果20 t,其中甲地需要水果22 t,乙地需要水果18 t,从A水果市场到甲地运费为50元/t,到乙地为30元/t;从B水果市场到甲地运费为60元/t,到乙地为45元/t.
(1)设A水果市场运送x(t)水果到甲地,请完成下表:
运往甲地(单位︰吨) 运往乙地(单位:吨)
A x
B
(2)设总运费为y元,请写出y关于x的函数表达式,求出自变量x的取值范围,并在平面直角坐标系中画出此函数的图象. 【出处:21教育名师】
(3)当A,B两个水果市场向甲、乙两地运送水果各多少吨时,总运费最少?最少是多少?
13.如图1,直线AB:y= x+4分别与x轴、y轴交于A、B两点,过点B的直线交x轴负半轴于点C , 将△BOC沿BC折叠,使点O落在BA上的点M处.
(1)求A、B两点的坐标;
(2)求线段BC的长;
(3)点P为x轴上的动点,当∠PBA=45°时,求点P的坐标.
14.如图,已知过点B(1,0)的直线 与直线 :y=2x+4相交于点P(-1,a).
(1)(1)求直线 的解析式;
(2)(2)求四边形PAOC的面积.
15.如图,l1表示某商场一天的手提电脑销售额与销售量的关系,l2表示该商场一天的销售成本与手提电脑销售量的关系.
(1)当销售量x=2时,销售额=________万元,销售成本=________万元,利润(收入-成本)________=万元.
(2)一天销售________台时,销售额等于销售成本.
(3)当销售量________时,该商场赢利(收入大于成本),当销售量________时,该商场亏损(收入小于成本).
(4)l1对应的函数表达式是________.
(5)写出利润与销售额之间的函数表达式________.
答案解析部分
一、单选题
1.【答案】 A
解: 是一次函数;
自变量次数不为1,故不是一次函数;
自变量次数不为1,故不是一次函数;
是常数;
是一次函数.
所以一次函数是 .
故答案为:A.
2.【答案】 D
解:令x=0,则y=2,令x=1,则y=-1,由此可画出一次函数的图象如下:
由图可知一次函数 y=?3x+2 的图象经过第一、二、四象限,
故答案为:D.
3.【答案】 B
解:∵正比例函数y=kx经过点(2,-3)
?∴-3=2k,
?∴k=-;
?∴正比例函数的解析式是y=-x;
A、∵当x=时,y≠-1,∴点(?,﹣1)不在该函数图象上;
B、∵当x=时,y=-1,∴点(? , ﹣1)在该函数图象上;
C、∵当x=-3时, y≠2,∴点(-3? ,2)不在该函数图象上;
D、∵当x=-时, y≠1,∴点(-? ,1)不在该函数图象上.
故答案为:B
4.【答案】 B
解:∵正比例函数y=kx中,k>0,
∴此函数是增函数.
∵x1>x2 ,
∴y1>y2 .
故答案为:B.
5.【答案】 A
解:直线 向上平移 个单位得到的直线解析式是 .
故答案为:A.
6.【答案】 A
解:由_é??????????????m_-3<0,
解得m<3.
故答案为:A.
二、填空题
7.【答案】 y=5-6x
解: _??±é????????y???_x之间的函数关系式为:y=5-6x.
故答案为:y=5-6x.
8.【答案】 4
解:设正比例函数为y=kx,
将点 代入得:4k=8,解得:k=2,
∴y=2x,
将点 代入得:2m=8,解得m=4,
故答案为:4.
9.【答案】 2
解:将P1(a,7),P2(a+1,9)代入y=kx+7中,得
②-①,得k=2.
故答案为:2.
10.【答案】 <
解:由一次函数 可得:k=3>0,
∴y随x的增大而增大,
∵函数图像经过 , 两点,
∴ ,
故答案为<.
三、综合题
11.【答案】 解:∵△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,
∴y=180°-60°-x,整理得:
y=120°-x( ),
将y=0和x=0两个值代入解析式,得到图像与坐标轴的两个交点坐标分别为(0,120),(120,0)画出图像如下:2-1-c-n-j-y
12.【答案】 (1)解:A地运_????????°???é?????_20-x,B地运往甲地的量为22-x,B地运往乙地的量为20-(22-x)=x-2,
如下所示: 21教育名师原创作品
? 运往甲地(单位︰吨) 运往乙地(单位:吨)
A x 20-x
B 22-x x-2
(2)解:y=50x+30(20-x)+60(22-x)+45(x-2)=5x+1830.
∵A、B到两地运送的水果量为非负数,
∴x≥0,20-x≥0,22-x≥0,x-2≥0,
∴2≤x≤20,
∴ 函数表达式为y=5x+1830(2≤x≤20).
函数图像如下所示:
(3)解:∵y=5x+1830(2≤x≤20)中,y随x的增大而增大,
∴当x=2时,总运费最少,
∴当A水果市场向甲、乙两地各运送2吨、18吨,B水果市场向甲、乙两地各运送20吨、0吨时,总运费最少,最少为1840元. 21世纪教育网版权所有
13.【答案】 (1)解: y=x+4,当x=0时,y=4,当y=0时,x=-3,
∴ A(-3,0),B(0,4) ;
(2)解: 由折叠得,CM=CO,∠CMB=∠BOC=90°,BM=OB=4,
∴AC=OA-OC=3-OC,
在Rt△AOB中,OA=3,OB=4,∴AB=5,
∴AM=AB-BM=1,
在Rt△AMC中,CM2+AM2=AC2 , 即OC2+12=(3-OC)2 ,
解得OC=,
∴BC==;
(3)解: 设P(m,0),∴PB=,
点P到AB的距离为d==,
∵∠PBA=45°,∴BP=, 即得=×,
解得m=-28或m=,
∴ P(-28,0)或(??,0) .
14.【答案】 (1)解:∵点p(-1,a)在直线l2:y=2x+4上,
? ∴2×(-1)+4=a? 解得a=2
? 则P的坐标为(-1,2),
设直线l1的解析式为:y=kx+b(k≠0),那么
? 解得:
?∴l1的解析式为:y=-x+1
(2)解:∵直线l1与y轴相交于点C,
∴C的坐标为(0,1),
又 直线l2与x轴相交于点A,
?∴A点的坐标为(-2,0),则AB=3
? 而
∴
15.【答案】 (1)2;3;-1
(2)4
(3)大于4;小于4
(4)y=x
(5)
解:(1)如图,∵ 过点(0,0),(4,4),
∴设l1的解析式为y=kx,
∴k=1,
∴直线 为:y=x,
∵ 过点(0,2),(4,4),
∴直线 为:y= x+2,
把x=2代入 :y=2,
把x=2代入 :y= 2+2=3,
∴销售额=2,销售成本=3,利润=-1
故答案为:2;3;-1
( 2 )如图可得x=4,
故答案为:4;
( 3 )如图可得,x 4时,该商场赢利,当x 4时,该商场亏损.
故答案为:大于4,小于4
( 4 )由(1)可知:y=x
( 5 )设销售x台时的利润为y万元,则:
当x=2时,y=2-3=-1当x=4时,y=4-4=0
所以 ,解得 ,
∴
_21?????????è?????(www.21cnjy.com)_
