17.4 反比例函数 同步练习(含解析)
文档属性
| 名称 | 17.4 反比例函数 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第17章 17.4 反比例函数
一、单选题
1.下列函数是y关于x的反比例函数的是(?? )
A.?y=??????????????????????????????B.?y= ??????????????????????????????C.?y=﹣ ??????????????????????????????D.?y=﹣
2.若 是反比例函数,则m满足的条件是(?? )
A.?m≠0????????????????????????????B.?m=3????????????????????????????C.?m=3或m=0????????????????????????????D.?m≠3且m≠0
3.反比例函数 的图象如图,A(-2,y1)、B(-1,y2)、C(1,y3)三点都在该反比例函数的图象上,则y1、y2、y3的大小关系是(?? ) 【来源:21·世纪·教育·网】
A.?y1<y2<y3???????????????????????B.?y2<y1<y3???????????????????????C.?y3<y2<y1???????????????????????D.?y3<y1<y2
4.已知反比例函数 ,下列结论中不正确的是(?? )
A.?图象必经过点 ????????????????????????????????????????B.?图象位于第二、四象限
C.?若 ,则0< ???????????????????????????????????D.?在每一个象限内, 随 值的增大而减小
5.如果反比例函数 的图象在第一、三象限内,则下列说法正确的是(??? )
A.?随 的增大而减小??????????????????????????????????????????B.?随 的增大而增大
C.?的取值范围为 ?????????????????????????????????????????D.?的取值范围是 21世纪教育网版权所有
6.近似眼镜的度数 (度)与镜片焦距 (米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距 的取值范围是(??? ) 21·世纪*教育网
A.?0米 米???????????????B.?米???????????????C.?0米 米???????????????D.?米
7.在反比例函数 图像上有两点 , , , ,则m的取值范围是(??? ). www-2-1-cnjy-com
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
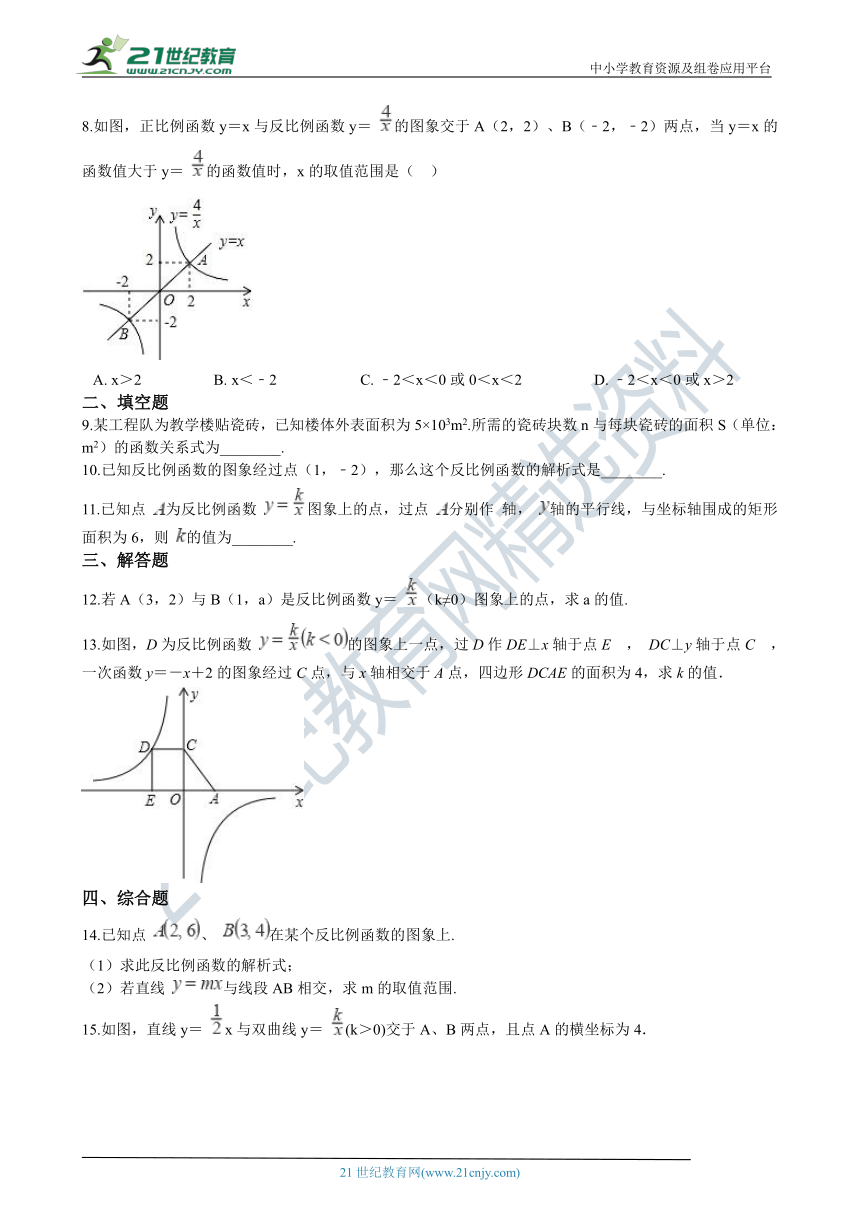
8.如图,正比例函数y=x与反比例函数y= 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于y= 的函数值时,x的取值范围是(?? ) 2-1-c-n-j-y
A.?x>2???????????????????B.?x<﹣2??????????????????????C.?﹣2<x<0或0<x<2???????????????????D.?﹣2<x<0或x>2
二、填空题
9.某工程队为教学楼贴_??·???????·???????_体外表面积为5×103m2.所需的瓷砖块数n与每块瓷砖的面积S(单位:m2)的函数关系式为________. 【出处:21教育名师】
10.已知反比例函数的图象经过点(1,﹣2),那么这个反比例函数的解析式是________.
11.已知点 为反比例函数 图象上的点,过点 分别作 轴, 轴的平行线,与坐标轴围成的矩形面积为6,则 的值为________. 【版权所有:21教育】
三、解答题
12.若A(3,2)与B(1,a)是反比例函数y= (k≠0)图象上的点,求a的值.
13.如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
四、综合题
14.已知点 、 在某个反比例函数的图象上.
(1)求此反比例函数的解析式;
(2)若直线 与线段AB相交,求m的取值范围.
15.如图,直线y= x与双曲线y= (k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y= (k>0)上一点C的纵坐标为8,求△AOC的面积.
(3)若 ,直接写出x的取值范围.
答案解析部分
一、单选题
1.【答案】 C
解:A、此函数不是反比例函数,故A不符合题意;
B、此函数不是反比例函数,故B不符合题意;
C、此函数是反比例函数,故C符合题意;
D、此函数是一次函数,故D不符合题意;
故答案为:C.
2.【答案】 D
解:由反比例函数的概念可得:m(m-3)≠0,
解得m≠0且m≠3.
故答案为:D.
3.【答案】 D
解:由图_è±??????????y1_>0,y2>0,y3<0,
∵当x<0时,y随x的增大而增大,-2<-1,
∴y1 ∴y3 故答案为:D.
4.【答案】 D
解:A、当x=-3时,y=? =2,所以点(-3,2)在函数y=? 的图象上,所以A选项的结论正确,不符合题意; 【来源:21cnj*y.co*m】
B、反比例函数y=? 分布在第二、四象限,所以B选项的结论正确,不符合题意;
C、若x<-2,则0<y<3,所以C选项的结论正确,不符合题意;
D、在每一个象限内,y随着x的增大而增大,所以D选项的结论不正确,符合题意.
故答案为:D.
5.【答案】 D
解:∵反比例函数 的图象在第一、三象限内,
∴ ,即 ,故C不符合题意,D符合题意,
∴在每个象限内,y随着x的增大而减小,故A、B不符合题意.
故答案为:D.
6.【答案】 B
解:设反比例函数的解析式为 ,
由题意,将点 代入得: ,解得 ,
则反比例函数的解析式为 ,
当 时, ,
在 范围内,y随x的增大而减小,
当 时, ,
即若要配制一副度数小于400度的近似眼镜,则镜片焦距 x 的取值范围是 米,
故答案为:B.
7.【答案】 B
解:∵ 时, ,
∴反比例函数图象在第一,三象限,
∴1?3m>0,
解得:m< .
故答案为:B.
8.【答案】 D
解:当﹣2<x<0或x>2时,y=x的函数值大于y= 的函数值.
故答案为:D.
二、填空题
9.【答案】 n=
解:由总面积除以每块瓷砖的面积等于瓷砖的块数可得,
n= = ,
故答案为:n= .
10.【答案】
解:设反比例函数的解析式为(k≠0),
∵反比例函数的图象经过点(1,﹣2),
∴k=-2×1=-2.
∴此函数解析式为.
故答案为:.
11.【答案】 ±6
解:由题,过点 A 分别作 x 轴, y 轴的平行线,与坐标轴围成的矩形面积等于 ,
∴ ,解得 ,
故答案为:±6.
三、解答题
12.【答案】 解:∵ A(3,2)与B(1,a)是反比例函数y= (k≠0)图象上的点
∴3×2=a=6.
故答案为:6. 2·1·c·n·j·y
13.【答案】 解:由于一次函数y=-x+2的图象经过C点,与x轴相交于A点,
则可求得A(2,0)、C(0,2),即OA=OC=2.
∴S△AOC= ×2×2=2,|k|=S矩形DCOE=4-2=2.
又函数图象位于第二象限,k<0,
则k=-2.
14.【答案】 (1)解:设所求的反比例函数的解析式是 ,
依题意得: ,
,
反比例函数为
(2)解:设 是线段AB上任一点,
则有 , ;,
,
,
所以m的取值范围是
15.【答案】 (1)解:∵点A的横坐标为4,点A在直线y= x上,
∴点A的纵坐标为y= ×4=2,即A(4,2).
又∵点A(4,2)在双曲线y= 上,
∴k=2×4=8;
(2)解:∵点C在双曲线y= 上,且点C纵坐标为8,
∴C(1,8).
如已知图,过点C作CM⊥x轴于M,过点A作AN⊥x轴于N.
∵S△COM= =4,
S△AON= =4,
S△AOC=S四边形OCAN- S△AON ,
S梯形CMNA=S四边形OCAN- S△COM ,
∴S△AOC=S梯形CMNA= ,
= ,
=15.
(3)解:根据图象,直线y= x与双曲线y= 的函数值大于0时,图象在第一象限,即x>0,
在交点A的左侧,直线y= x比双曲线y= 的函数值小,即x<4,
故当0<x<4时, .
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第17章 17.4 反比例函数
一、单选题
1.下列函数是y关于x的反比例函数的是(?? )
A.?y=??????????????????????????????B.?y= ??????????????????????????????C.?y=﹣ ??????????????????????????????D.?y=﹣
2.若 是反比例函数,则m满足的条件是(?? )
A.?m≠0????????????????????????????B.?m=3????????????????????????????C.?m=3或m=0????????????????????????????D.?m≠3且m≠0
3.反比例函数 的图象如图,A(-2,y1)、B(-1,y2)、C(1,y3)三点都在该反比例函数的图象上,则y1、y2、y3的大小关系是(?? ) 【来源:21·世纪·教育·网】
A.?y1<y2<y3???????????????????????B.?y2<y1<y3???????????????????????C.?y3<y2<y1???????????????????????D.?y3<y1<y2
4.已知反比例函数 ,下列结论中不正确的是(?? )
A.?图象必经过点 ????????????????????????????????????????B.?图象位于第二、四象限
C.?若 ,则0< ???????????????????????????????????D.?在每一个象限内, 随 值的增大而减小
5.如果反比例函数 的图象在第一、三象限内,则下列说法正确的是(??? )
A.?随 的增大而减小??????????????????????????????????????????B.?随 的增大而增大
C.?的取值范围为 ?????????????????????????????????????????D.?的取值范围是 21世纪教育网版权所有
6.近似眼镜的度数 (度)与镜片焦距 (米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距 的取值范围是(??? ) 21·世纪*教育网
A.?0米 米???????????????B.?米???????????????C.?0米 米???????????????D.?米
7.在反比例函数 图像上有两点 , , , ,则m的取值范围是(??? ). www-2-1-cnjy-com
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
8.如图,正比例函数y=x与反比例函数y= 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于y= 的函数值时,x的取值范围是(?? ) 2-1-c-n-j-y
A.?x>2???????????????????B.?x<﹣2??????????????????????C.?﹣2<x<0或0<x<2???????????????????D.?﹣2<x<0或x>2
二、填空题
9.某工程队为教学楼贴_??·???????·???????_体外表面积为5×103m2.所需的瓷砖块数n与每块瓷砖的面积S(单位:m2)的函数关系式为________. 【出处:21教育名师】
10.已知反比例函数的图象经过点(1,﹣2),那么这个反比例函数的解析式是________.
11.已知点 为反比例函数 图象上的点,过点 分别作 轴, 轴的平行线,与坐标轴围成的矩形面积为6,则 的值为________. 【版权所有:21教育】
三、解答题
12.若A(3,2)与B(1,a)是反比例函数y= (k≠0)图象上的点,求a的值.
13.如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
四、综合题
14.已知点 、 在某个反比例函数的图象上.
(1)求此反比例函数的解析式;
(2)若直线 与线段AB相交,求m的取值范围.
15.如图,直线y= x与双曲线y= (k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y= (k>0)上一点C的纵坐标为8,求△AOC的面积.
(3)若 ,直接写出x的取值范围.
答案解析部分
一、单选题
1.【答案】 C
解:A、此函数不是反比例函数,故A不符合题意;
B、此函数不是反比例函数,故B不符合题意;
C、此函数是反比例函数,故C符合题意;
D、此函数是一次函数,故D不符合题意;
故答案为:C.
2.【答案】 D
解:由反比例函数的概念可得:m(m-3)≠0,
解得m≠0且m≠3.
故答案为:D.
3.【答案】 D
解:由图_è±??????????y1_>0,y2>0,y3<0,
∵当x<0时,y随x的增大而增大,-2<-1,
∴y1
4.【答案】 D
解:A、当x=-3时,y=? =2,所以点(-3,2)在函数y=? 的图象上,所以A选项的结论正确,不符合题意; 【来源:21cnj*y.co*m】
B、反比例函数y=? 分布在第二、四象限,所以B选项的结论正确,不符合题意;
C、若x<-2,则0<y<3,所以C选项的结论正确,不符合题意;
D、在每一个象限内,y随着x的增大而增大,所以D选项的结论不正确,符合题意.
故答案为:D.
5.【答案】 D
解:∵反比例函数 的图象在第一、三象限内,
∴ ,即 ,故C不符合题意,D符合题意,
∴在每个象限内,y随着x的增大而减小,故A、B不符合题意.
故答案为:D.
6.【答案】 B
解:设反比例函数的解析式为 ,
由题意,将点 代入得: ,解得 ,
则反比例函数的解析式为 ,
当 时, ,
在 范围内,y随x的增大而减小,
当 时, ,
即若要配制一副度数小于400度的近似眼镜,则镜片焦距 x 的取值范围是 米,
故答案为:B.
7.【答案】 B
解:∵ 时, ,
∴反比例函数图象在第一,三象限,
∴1?3m>0,
解得:m< .
故答案为:B.
8.【答案】 D
解:当﹣2<x<0或x>2时,y=x的函数值大于y= 的函数值.
故答案为:D.
二、填空题
9.【答案】 n=
解:由总面积除以每块瓷砖的面积等于瓷砖的块数可得,
n= = ,
故答案为:n= .
10.【答案】
解:设反比例函数的解析式为(k≠0),
∵反比例函数的图象经过点(1,﹣2),
∴k=-2×1=-2.
∴此函数解析式为.
故答案为:.
11.【答案】 ±6
解:由题,过点 A 分别作 x 轴, y 轴的平行线,与坐标轴围成的矩形面积等于 ,
∴ ,解得 ,
故答案为:±6.
三、解答题
12.【答案】 解:∵ A(3,2)与B(1,a)是反比例函数y= (k≠0)图象上的点
∴3×2=a=6.
故答案为:6. 2·1·c·n·j·y
13.【答案】 解:由于一次函数y=-x+2的图象经过C点,与x轴相交于A点,
则可求得A(2,0)、C(0,2),即OA=OC=2.
∴S△AOC= ×2×2=2,|k|=S矩形DCOE=4-2=2.
又函数图象位于第二象限,k<0,
则k=-2.
14.【答案】 (1)解:设所求的反比例函数的解析式是 ,
依题意得: ,
,
反比例函数为
(2)解:设 是线段AB上任一点,
则有 , ;,
,
,
所以m的取值范围是
15.【答案】 (1)解:∵点A的横坐标为4,点A在直线y= x上,
∴点A的纵坐标为y= ×4=2,即A(4,2).
又∵点A(4,2)在双曲线y= 上,
∴k=2×4=8;
(2)解:∵点C在双曲线y= 上,且点C纵坐标为8,
∴C(1,8).
如已知图,过点C作CM⊥x轴于M,过点A作AN⊥x轴于N.
∵S△COM= =4,
S△AON= =4,
S△AOC=S四边形OCAN- S△AON ,
S梯形CMNA=S四边形OCAN- S△COM ,
∴S△AOC=S梯形CMNA= ,
= ,
=15.
(3)解:根据图象,直线y= x与双曲线y= 的函数值大于0时,图象在第一象限,即x>0,
在交点A的左侧,直线y= x比双曲线y= 的函数值小,即x<4,
故当0<x<4时, .
_21?????????è?????(www.21cnjy.com)_
