18.1 平行四边形的性质 同步练习(含解析)
文档属性
| 名称 | 18.1 平行四边形的性质 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第18章 18.1 平行四边形的性质
一、单选题
1.在平行四边形 中,若 ,则 的度数是(? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
2.如图,平面直角坐标系中O是原点,平行四边形ABCO的顶点A、C的坐标分别(8,0)、(3,4),点D,E把线段OB三等分,延长CD,CE分别交OA,AB于点F,G,连接FG,则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是 ;④ .正确的个数是(? )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
3.如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是(?? )
A.?①②③④?????????????????????????????????B.?①④?????????????????????????????????C.?②③?????????????????????????????????D.?①②③
4.如图,在平行四边形AB_CD?????????B_=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有(?? ) 【出处:21教育名师】
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
5.如图,E是?ABCD的边AD上的一点,连接BE并延长,交CD的延长线于点F,若AE: BC =3: 5,则FD: DC的值为(? ) 【版权所有:21教育】
A.?2 : 3??????????????????????????????????B.?2:5??????????????????????????????????C.?3 : 4??????????????????????????????????D.?3 : 5
6.如图,平行四边形 的对角线 , 相交于点 , 为 的中点,连接 交 于点 ,若 ,则 的长为(? ) 21教育名师原创作品
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
7.如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E , 交DC的延长线于点F , BG⊥AE , 垂足为G , BG= ,则△CEF的周长为(??? ) 21*cnjy*com
A.?8????????????????????????????????????????B.?9.5????????????????????????????????????????C.?10????????????????????????????????????????D.?11.5
二、填空题
8.如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若 , ,则 等于________.
9.如图,在平行四边形 中, 平分 , , ,则 的周长是________.
10.如图,在平行四_è?????ABCD_中,点M为边AD上一点,AM=2MD,点E,点F分别是BM,CM中点,若EF=6,则AM的长为________.
11.如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取________.
三、解答题
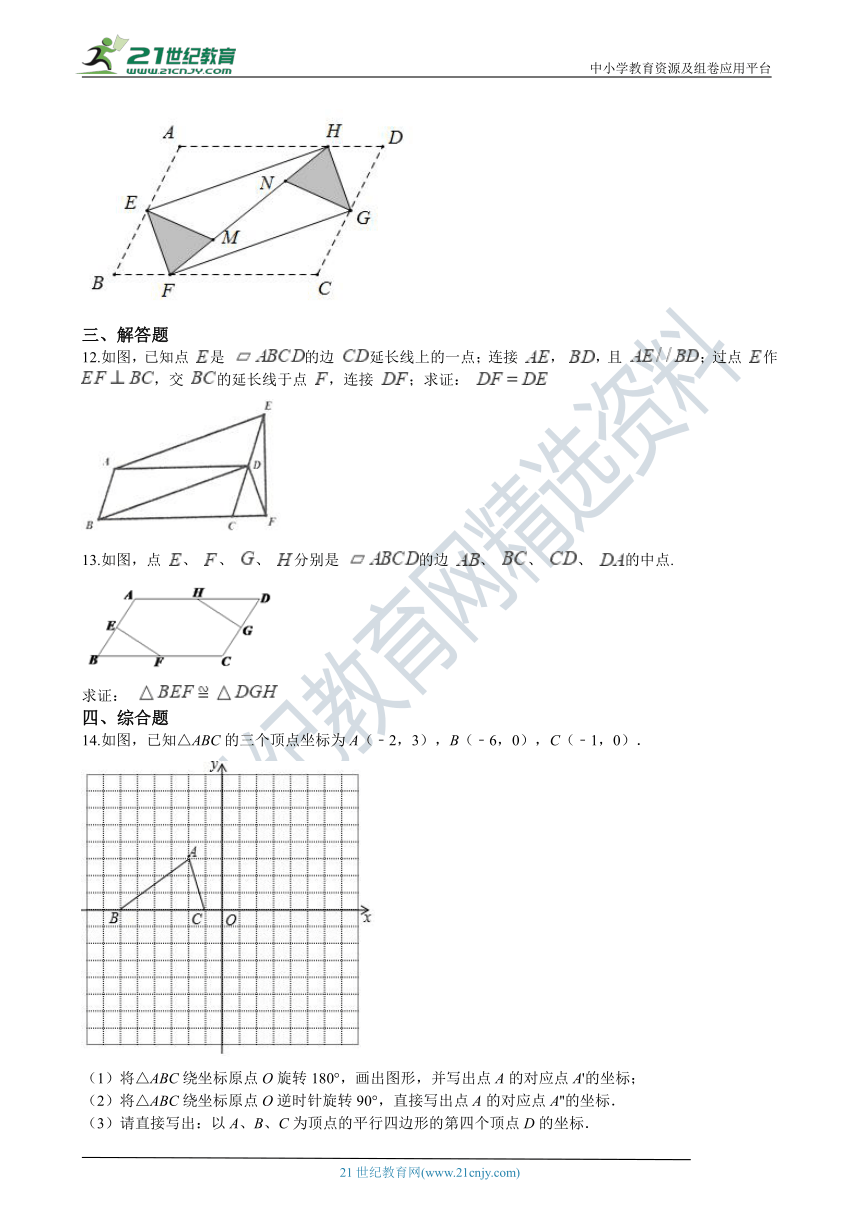
12.如图,已知点 是 的边 延长线上的一点;连接 , ,且 ;过点 作 ,交 的延长线于点 ,连接 ;求证:
13.如图,点 、 、 、 分别是 的边 、 、 、 的中点.
求证:
四、综合题
14.如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A'的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点A''的坐标.
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
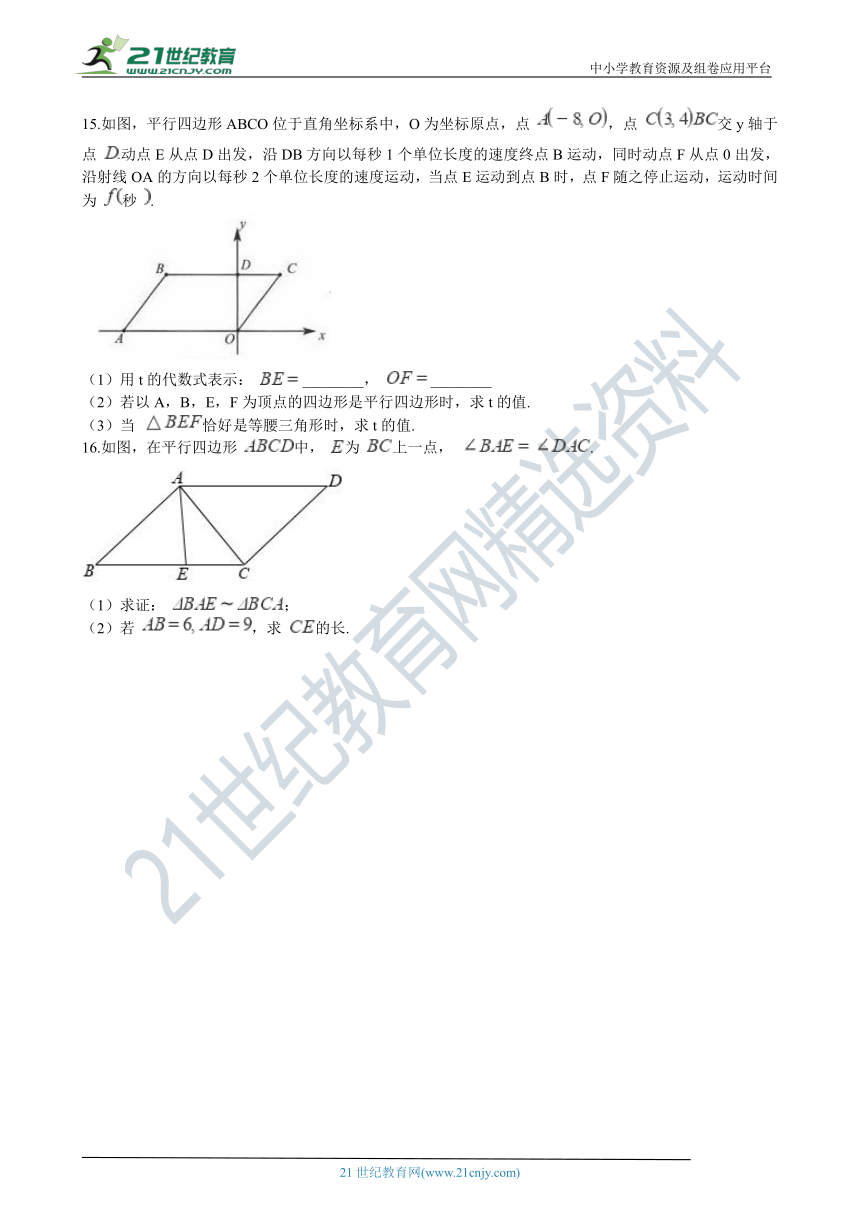
15.如图,平行四边形ABCO位于直角坐标系中,O为坐标原点,点 ,点 交y轴于点 动点E从点D出发,沿DB方向以每秒1个单位长度的速度终点B运动,同时动点F从点0出发,沿射线OA的方向以每秒2个单位长度的速度运动,当点E运动到点B时,点F随之停止运动,运动时间为 秒 .
(1)用t的代数式表示: ________, ________
(2)若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.
(3)当 恰好是等腰三角形时,求t的值.
16.如图,在平行四边形 中, 为 上一点, .
(1)求证: ;
(2)若 ,求 的长.
答案解析部分
一、单选题
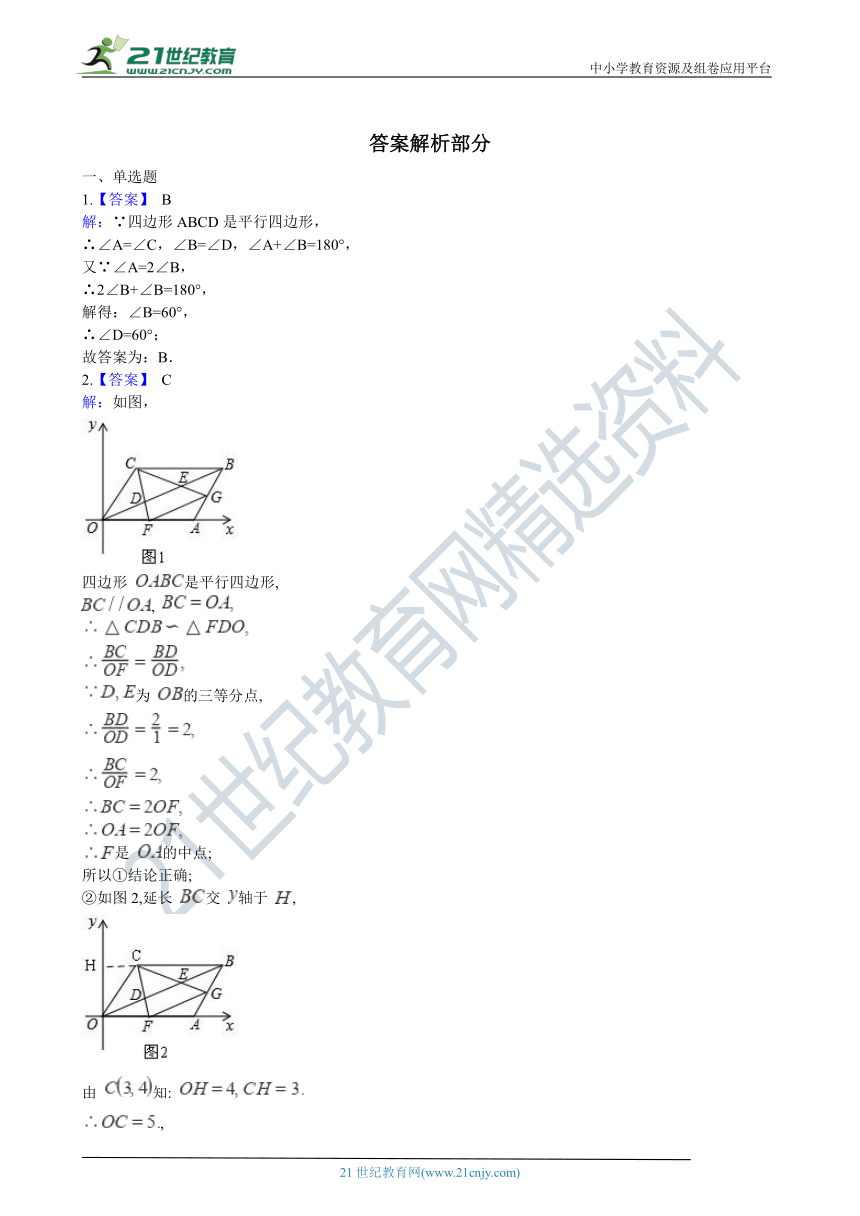
1.【答案】 B
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,∠A+∠B=180°,
又∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°,
∴∠D=60°;
故答案为:B.
2.【答案】 C
解:如图,
四边形 是平行四边形,
,
为 的三等分点,
是 的中点;
所以①结论正确;
②如图2,延长 交 轴于 ,
由 知:
,
,
不成立,
所以②结论不正确;
③由①知: 是 的中点,
同理得: 是 的中点,
?
是 的中位线,
,
过 作 于
,
设四边形DEGF的面积为
所以③结论正确;
④在 中,由勾股定理得:
所以④结论不正确;
故本题结论正确的有:①③;
故答案为:C.
3.【答案】 D
解:∵在?ABCD中, ,
∵点E是OA的中点,
,
∵AD//BC,
∴△AFE∽△CBE,
,
∵AD=BC,
,
;故①正确;
∵S△AEF=4, ,
∴S△BCE=36;故②正确;
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故答案为:泽:D.?
4.【答案】 B
解:∵将△ABC沿对角线AC折叠,点B的对应点落在点E处,
∴∠E=∠B=60°,
∴△BEC是等边三角形,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠D=∠B=60°,
∴∠B=∠EAF=60°,
∴△EFA是等边三角形,
∵∠EFA=∠DFC=60°,∠D=∠B=60°,
∴△DFC是等边三角形,
∴图中等边三角形共有3个,
故答案为:B.
5.【答案】 A
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,AB=CD,AD=BC,
∴ED:AE=EF:EB,FD:DC=EF:EB,
∴FD: DC= ED:AE
∵AE: BC=3:5,AD=BC,
∴AE:AD=3:5,
∴ED:AE =2:3,
∴FD: DC=2:3,
故答案为:A.
6.【答案】 B
解:∵点E是BC中点,
∴BC=2BE,
∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,BO=OD,
∴AD=2BE,
设BF=a,
∵OF=1,
∴BO=DO=a+1,
则DF=a+2,
∵BC∥AD
∴△BEF∽△DAF,
∴
解得a=2,
经检验a=2是原方程的解
∴BF=2,
∴BO=DO=3,
∴BD=6
故答案为:B.
7.【答案】 A
解:∵在?ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DC,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴AD=FD,
∴△ADF是等腰三角形,
同理△ABE是等腰三角形,
AD=DF=9;
∵AB=BE=6,
∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG=4 ,可得:AG=2,
又BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵四边形ABCD为平行四边形,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故答案为:A.
二、填空题
8.【答案】 12
解:在平行四边形ABCD中, ,
∽ ,
,
又 ,
,
而 ,
,
,
,
故答案为:12.
9.【答案】 16
解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=5,BE=2,
∴AD=BC=5,
∴CE=BC?BE=5?2=3,
∴CD=AB=3,
∴?ABCD的周长=5+5+3+3=16.
故答案为:16.
10.【答案】 8
解:∵点E,点F分别是BM,CM中点,
∴EF是△BCM的中位线,
∴ ,
∵四边形ABCD是平行四边形,
∴ ,
又∵ ,
∴ .
故答案是:8.
11.【答案】
解:如图,作BP⊥AD,交DA延长线于P,作BQ∥FH,交AD于Q.
由题意得,AE=EM=BE= AB=4cm,DG=NG=CG=?CD=4cm,
AH=MH,BF=MF,
∵四边形 为矩形,
∴EF=HG,EF∥HG
∵四边形ABCD为平行四边形,
∴∠EBF=∠GDH=60°
∵EF∥HG
∴∠EFM=∠GHN,
又∵∠EFM=∠EFB,∠GHD =∠GHN,
∴∠EFB=∠GHD,
∴△BEF≌△DGH,
∴DH=BF,
∴FH=FM+HM=BF+AH=10cm,
∵BQ∥FH,BF∥QH,
∴BQ=HF=10cm,
∵PD∥BC,
∴∠PAB=∠ABC=60°,
∴在Rt△ABP中,∠ABP=30°,
∴AP= AB=4cm,
∴BP= cm,
设AH=xcm,则HD=(10-x)cm,
∴PQ=14-2(10-x)=(2x-6)cm,
在Rt△BPQ中,根据勾股定理得
解得 (不合题意,舍去)
故答案为:
三、解答题
12.【答案】 证明:∵四边形 是平行四边形,
∴ , ,
又∵
∴四边形 是平行四边形;
∴ ,即 ;
又 于点 ;∴∠EFC=90°
∴在 中,点 是斜边 的中点
∴ .
13.【答案】 证明:∵四边形 是平行四边形
∴ , ,
∵点 、 、 、 分别是 、 、 、 的中点
∴ , , ,
∴ ,
在 和 中
∴
四、综合题
14.【答案】 (1)如图所示:△A′B′C′,即为所求,A′(2,﹣3);
故答案为:(2,﹣3);
(2)如图,A″的坐标为(﹣3,﹣2);
故答案为:(﹣3,﹣2);
(3)如图,第四个顶点D的坐标为(3,3)或(﹣7,3)或(﹣5,﹣3).
故答案为:(3,3)或(﹣7,3)或(﹣5,﹣3).
15.【答案】 (1)5-t;OF=12t
(2)解: 当F在A点右侧,四边形ABEF为平行四边形, , 21*cnjy*com
即 ,解得 ,
当P在A点左侧,四边形BEAF为平行四边形, ,即 ,
解得 ;
(3)解:当 恰好是等腰三角形时,有以下三种情况:
当 时, ,解得 ;
当 时, ,方程无解;
当 时, ,解得 ;
所以,当 或 时,当 恰好是等腰三角形.
16.【答案】 (1)证明:∵四边形 是平行四边形,
∴ ,
∴ ,
∵ ,
∴
又∵ ,
∴
(2)解:∵四边形 是平行四边形
∴ ,
由(1)知: ,
∴ ,
∴ ,
∴ ,
∴
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第18章 18.1 平行四边形的性质
一、单选题
1.在平行四边形 中,若 ,则 的度数是(? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
2.如图,平面直角坐标系中O是原点,平行四边形ABCO的顶点A、C的坐标分别(8,0)、(3,4),点D,E把线段OB三等分,延长CD,CE分别交OA,AB于点F,G,连接FG,则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是 ;④ .正确的个数是(? )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
3.如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是(?? )
A.?①②③④?????????????????????????????????B.?①④?????????????????????????????????C.?②③?????????????????????????????????D.?①②③
4.如图,在平行四边形AB_CD?????????B_=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有(?? ) 【出处:21教育名师】
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
5.如图,E是?ABCD的边AD上的一点,连接BE并延长,交CD的延长线于点F,若AE: BC =3: 5,则FD: DC的值为(? ) 【版权所有:21教育】
A.?2 : 3??????????????????????????????????B.?2:5??????????????????????????????????C.?3 : 4??????????????????????????????????D.?3 : 5
6.如图,平行四边形 的对角线 , 相交于点 , 为 的中点,连接 交 于点 ,若 ,则 的长为(? ) 21教育名师原创作品
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
7.如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E , 交DC的延长线于点F , BG⊥AE , 垂足为G , BG= ,则△CEF的周长为(??? ) 21*cnjy*com
A.?8????????????????????????????????????????B.?9.5????????????????????????????????????????C.?10????????????????????????????????????????D.?11.5
二、填空题
8.如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若 , ,则 等于________.
9.如图,在平行四边形 中, 平分 , , ,则 的周长是________.
10.如图,在平行四_è?????ABCD_中,点M为边AD上一点,AM=2MD,点E,点F分别是BM,CM中点,若EF=6,则AM的长为________.
11.如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取________.
三、解答题
12.如图,已知点 是 的边 延长线上的一点;连接 , ,且 ;过点 作 ,交 的延长线于点 ,连接 ;求证:
13.如图,点 、 、 、 分别是 的边 、 、 、 的中点.
求证:
四、综合题
14.如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A'的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点A''的坐标.
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
15.如图,平行四边形ABCO位于直角坐标系中,O为坐标原点,点 ,点 交y轴于点 动点E从点D出发,沿DB方向以每秒1个单位长度的速度终点B运动,同时动点F从点0出发,沿射线OA的方向以每秒2个单位长度的速度运动,当点E运动到点B时,点F随之停止运动,运动时间为 秒 .
(1)用t的代数式表示: ________, ________
(2)若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.
(3)当 恰好是等腰三角形时,求t的值.
16.如图,在平行四边形 中, 为 上一点, .
(1)求证: ;
(2)若 ,求 的长.
答案解析部分
一、单选题
1.【答案】 B
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,∠A+∠B=180°,
又∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°,
∴∠D=60°;
故答案为:B.
2.【答案】 C
解:如图,
四边形 是平行四边形,
,
为 的三等分点,
是 的中点;
所以①结论正确;
②如图2,延长 交 轴于 ,
由 知:
,
,
不成立,
所以②结论不正确;
③由①知: 是 的中点,
同理得: 是 的中点,
?
是 的中位线,
,
过 作 于
,
设四边形DEGF的面积为
所以③结论正确;
④在 中,由勾股定理得:
所以④结论不正确;
故本题结论正确的有:①③;
故答案为:C.
3.【答案】 D
解:∵在?ABCD中, ,
∵点E是OA的中点,
,
∵AD//BC,
∴△AFE∽△CBE,
,
∵AD=BC,
,
;故①正确;
∵S△AEF=4, ,
∴S△BCE=36;故②正确;
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故答案为:泽:D.?
4.【答案】 B
解:∵将△ABC沿对角线AC折叠,点B的对应点落在点E处,
∴∠E=∠B=60°,
∴△BEC是等边三角形,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠D=∠B=60°,
∴∠B=∠EAF=60°,
∴△EFA是等边三角形,
∵∠EFA=∠DFC=60°,∠D=∠B=60°,
∴△DFC是等边三角形,
∴图中等边三角形共有3个,
故答案为:B.
5.【答案】 A
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,AB=CD,AD=BC,
∴ED:AE=EF:EB,FD:DC=EF:EB,
∴FD: DC= ED:AE
∵AE: BC=3:5,AD=BC,
∴AE:AD=3:5,
∴ED:AE =2:3,
∴FD: DC=2:3,
故答案为:A.
6.【答案】 B
解:∵点E是BC中点,
∴BC=2BE,
∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,BO=OD,
∴AD=2BE,
设BF=a,
∵OF=1,
∴BO=DO=a+1,
则DF=a+2,
∵BC∥AD
∴△BEF∽△DAF,
∴
解得a=2,
经检验a=2是原方程的解
∴BF=2,
∴BO=DO=3,
∴BD=6
故答案为:B.
7.【答案】 A
解:∵在?ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DC,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴AD=FD,
∴△ADF是等腰三角形,
同理△ABE是等腰三角形,
AD=DF=9;
∵AB=BE=6,
∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG=4 ,可得:AG=2,
又BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵四边形ABCD为平行四边形,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故答案为:A.
二、填空题
8.【答案】 12
解:在平行四边形ABCD中, ,
∽ ,
,
又 ,
,
而 ,
,
,
,
故答案为:12.
9.【答案】 16
解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=5,BE=2,
∴AD=BC=5,
∴CE=BC?BE=5?2=3,
∴CD=AB=3,
∴?ABCD的周长=5+5+3+3=16.
故答案为:16.
10.【答案】 8
解:∵点E,点F分别是BM,CM中点,
∴EF是△BCM的中位线,
∴ ,
∵四边形ABCD是平行四边形,
∴ ,
又∵ ,
∴ .
故答案是:8.
11.【答案】
解:如图,作BP⊥AD,交DA延长线于P,作BQ∥FH,交AD于Q.
由题意得,AE=EM=BE= AB=4cm,DG=NG=CG=?CD=4cm,
AH=MH,BF=MF,
∵四边形 为矩形,
∴EF=HG,EF∥HG
∵四边形ABCD为平行四边形,
∴∠EBF=∠GDH=60°
∵EF∥HG
∴∠EFM=∠GHN,
又∵∠EFM=∠EFB,∠GHD =∠GHN,
∴∠EFB=∠GHD,
∴△BEF≌△DGH,
∴DH=BF,
∴FH=FM+HM=BF+AH=10cm,
∵BQ∥FH,BF∥QH,
∴BQ=HF=10cm,
∵PD∥BC,
∴∠PAB=∠ABC=60°,
∴在Rt△ABP中,∠ABP=30°,
∴AP= AB=4cm,
∴BP= cm,
设AH=xcm,则HD=(10-x)cm,
∴PQ=14-2(10-x)=(2x-6)cm,
在Rt△BPQ中,根据勾股定理得
解得 (不合题意,舍去)
故答案为:
三、解答题
12.【答案】 证明:∵四边形 是平行四边形,
∴ , ,
又∵
∴四边形 是平行四边形;
∴ ,即 ;
又 于点 ;∴∠EFC=90°
∴在 中,点 是斜边 的中点
∴ .
13.【答案】 证明:∵四边形 是平行四边形
∴ , ,
∵点 、 、 、 分别是 、 、 、 的中点
∴ , , ,
∴ ,
在 和 中
∴
四、综合题
14.【答案】 (1)如图所示:△A′B′C′,即为所求,A′(2,﹣3);
故答案为:(2,﹣3);
(2)如图,A″的坐标为(﹣3,﹣2);
故答案为:(﹣3,﹣2);
(3)如图,第四个顶点D的坐标为(3,3)或(﹣7,3)或(﹣5,﹣3).
故答案为:(3,3)或(﹣7,3)或(﹣5,﹣3).
15.【答案】 (1)5-t;OF=12t
(2)解: 当F在A点右侧,四边形ABEF为平行四边形, , 21*cnjy*com
即 ,解得 ,
当P在A点左侧,四边形BEAF为平行四边形, ,即 ,
解得 ;
(3)解:当 恰好是等腰三角形时,有以下三种情况:
当 时, ,解得 ;
当 时, ,方程无解;
当 时, ,解得 ;
所以,当 或 时,当 恰好是等腰三角形.
16.【答案】 (1)证明:∵四边形 是平行四边形,
∴ ,
∴ ,
∵ ,
∴
又∵ ,
∴
(2)解:∵四边形 是平行四边形
∴ ,
由(1)知: ,
∴ ,
∴ ,
∴ ,
∴
_21?????????è?????(www.21cnjy.com)_
