18.2 平行四边形的判定 同步练习(含解析)
文档属性
| 名称 | 18.2 平行四边形的判定 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 15:12:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第18章 18.2 平行四边形的判定
一、单选题
1.下列命题中,正确的个数有(?? )
①若 ,则a、b中至少有一个是0.
②若S△ABC=S△ABD(C、D不重合),则CD∥AB。
③图象为直线的函数的解析式为一次函数。
④有一组对边相等和一组对角相等的四边形是平行四边形。
A.?0个??????????????????????????????????????B.?1个??????????????????????????????????????C.?2个??????????????????????????????????????D.?4 个
2.下列命题中,正确的是(??? )
A.?在三角形中,到三角形_???è??è·??????????_的点是三条边垂直平分线的交点???
B.?平行四边形是轴对称图形???
C.?三角形的中位线将三角形分成面积相等的两个部分???
D.?一组对边平行,一组对角相等的四边形是平行四边形21教育网
3.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为 、 、 ,若 =3, =8,则 的值为(?? ) 21·世纪*教育网
A.?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?44?????????????????????????????????????????D.?48
4.一个零件的形状如图所示, ,则 的度数是(?? )
A.?70°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
5.如图,在平面直角坐标系中,点 ,当四边形 ABCD 的周长最小时,则 m 的值为(?? ). www-2-1-cnjy-com
A.???????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?3
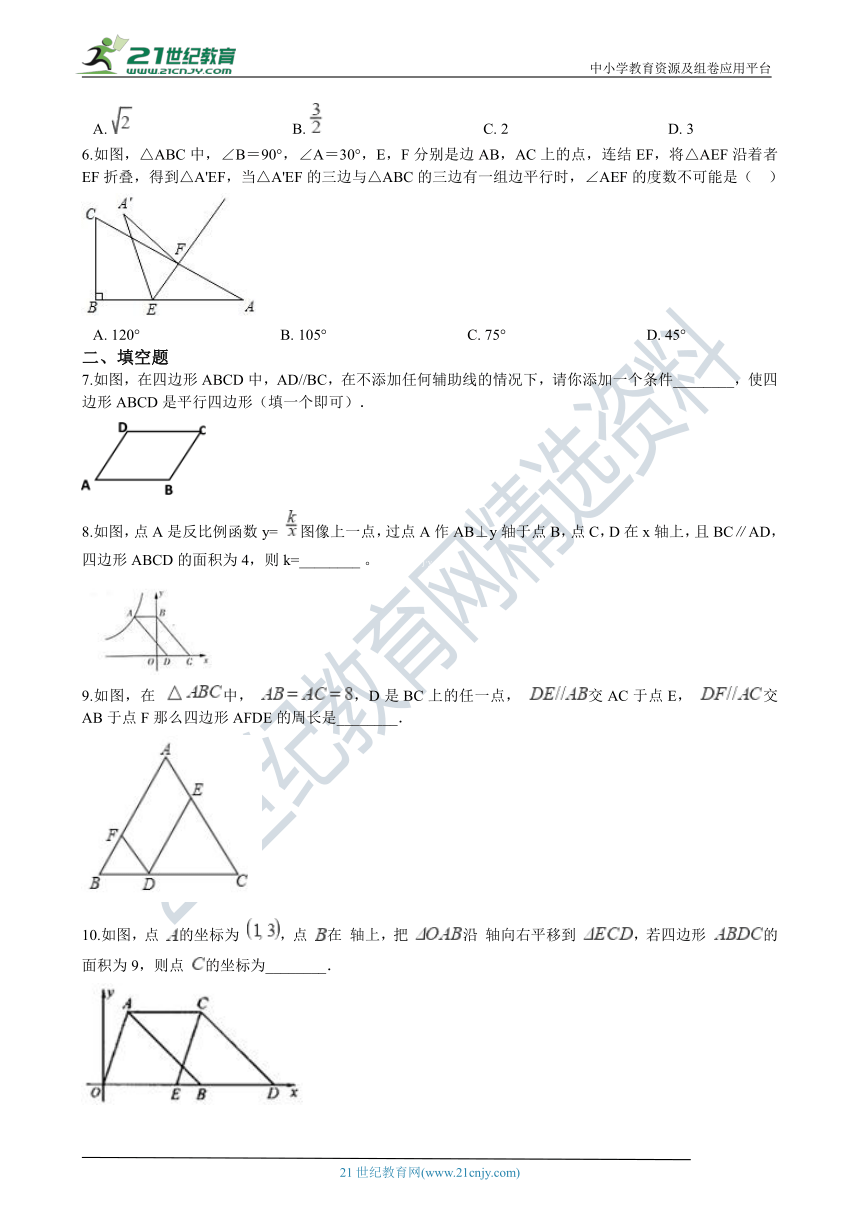
6.如图,△ABC中,∠_B???90?°???_∠A=30°,E,F分别是边AB,AC上的点,连结EF,将△AEF沿着者EF折叠,得到△A'EF,当△A'EF的三边与△ABC的三边有一组边平行时,∠AEF的度数不可能是(?? )
A.?120°?????????????????????????????????????B.?105°?????????????????????????????????????C.?75°?????????????????????????????????????D.?45°
二、填空题
7.如图,在四_è?????ABCD_中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件________,使四边形ABCD是平行四边形(填一个即可). 【来源:21cnj*y.co*m】
8.如图,点A是反比例函数y= 图像上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为4,则k=________?。 2·1·c·n·j·y
9.如图,在 中, ,D是BC上的任一点, 交AC于点E, 交AB于点F那么四边形AFDE的周长是________. 21教育名师原创作品
10.如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为________. 21*cnjy*com
三、综合题
11.如图都是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点.
(1)请在如图1,如图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等).
(2)如图1中所画的平行四边形的面积为________.
12.如图,在 ABC中, ,M是斜边AB的中点,AM=AN, .求证:MN=AC.
13.如图,平行四边形ABCD中_???AB???3c_m , BC=5cm , ∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F , 连结CE , DF .
(1)求证:四边形CEDF是平行四边形;
(2)当AE=________cm时,四边形CEDF是矩形.(直接写出答案,不需要说明理由)
14.如图, 中,点 , 分别是边 , 的中点,过点 作 交 的延长线于点 ,连结 .
(1)求证:四边形 是平行四边形.
(2)当 时,若 , ,求 的长.
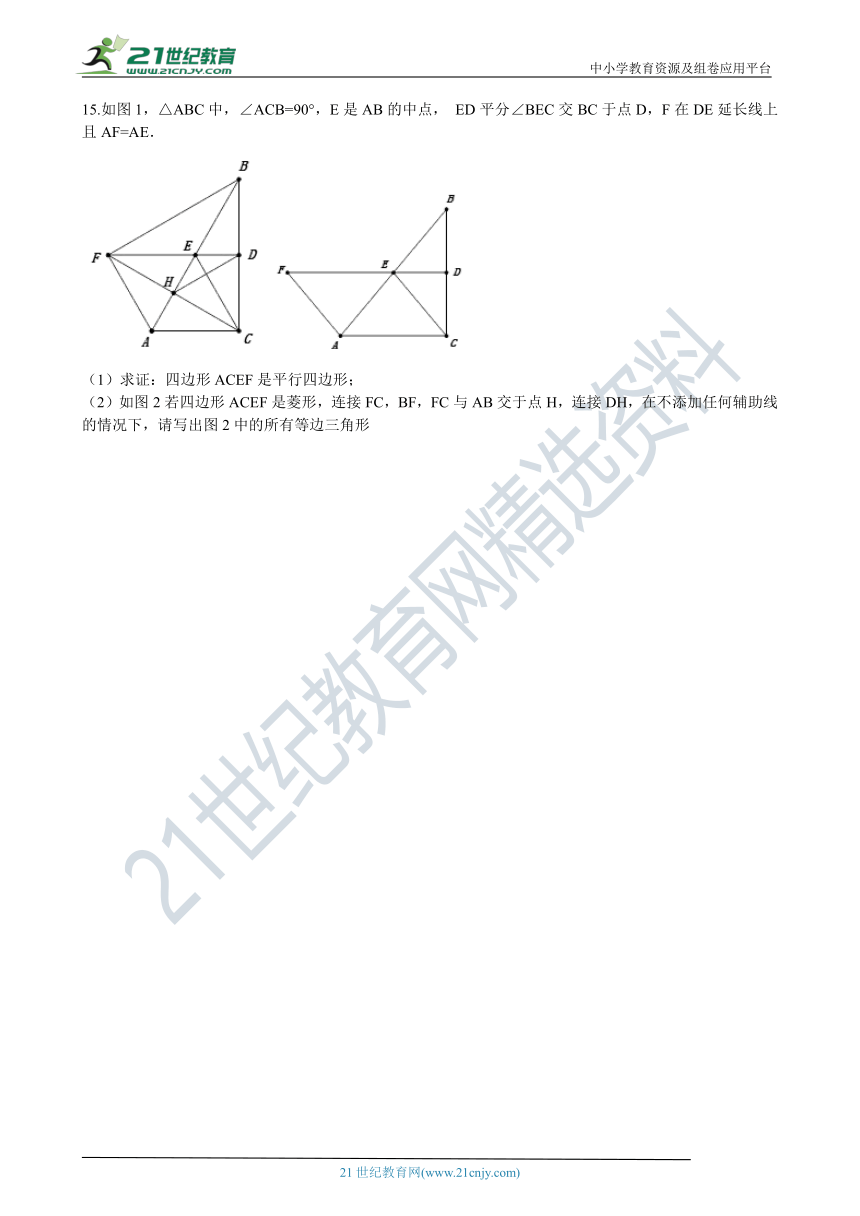
15.如图1,△ABC中,∠ACB=90°,E是AB的中点, ED平分∠BEC交BC于点D,F在DE延长线上且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)如图2若四边形ACE_F???è?±??????è??_接FC,BF,FC与AB交于点H,连接DH,在不添加任何辅助线的情况下,请写出图2中的所有等边三角形
答案解析部分
一、单选题
1.【答案】 B
解: ①若 ,则a、b中至少有一个是0,故①正确;
②若S△ABC=S△ABD(C、D不重合),当点C,D在AB的同一侧时,CD∥AB,当点C,D在AB的两侧时,AB不平行CD,故②错误;
③图象为直线的函数的解析式不一定为一次函数,比如直线x=2或直线y=5,它们不是一次函数,故③错误;
④有一组对边相等和一组对角相等的四边形不一定是平行四边形。故 ④错误;
正确的个数为1个.
故答案为:B.
2.【答案】 D
解:A、在三角_???????????°???è§?_形三边距离相等的点是三条角平分线的交点 ,故A不符合题意;
B、 平行四边形是中心对称图形,不是轴对称图形,故B不符合题意;
C、 三角形的中线将三角形分成面积相等的两个部分 ,故C不符合题意;
D、 一组对边平行,一组对角相等的四边形是平行四边形,故D符合题意. 21世纪教育网版权所有
故答案为:D.
3.【答案】 C
解:∵S1=3,S3=8
∴AB= ,CD=
过A作AE∥CD交BC于E
则∠AEB=∠DCB
∵AD∥BC
∴四边形AECD是平行四边形
∴CE=AD,AE=CD=
∵∠ABC+∠DCB=90°
∴∠AEB+∠ABC=90°
∴∠BAE=90°
∴BE=
∵BC=2AD
∴BC=2BE=
∴S2=
故答案为:C.
4.【答案】 B
解:延长DE与BC交于点F,如图:
∵ ,
∴四边形ABFD是平行四边形,
∴∠A=∠F,
在△BDF中, ,
∴ ,
∴∠A=80°;
故答案为:B.
5.【答案】 B
解:∵A(1,5),B(4,1),C(m,-m),D(m-3,-m+4),
∴ , ,
∴AB=CD,
∵点B向左平移3个单位,再向上平移4个单位得到A,点C向左平移3个单位,再向上平移4个单位得到D,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BC=AD,
故四边形ABCD的周长为2(AB+BC),而AB=5,故只要BC最短,则周长最短,
∴由点到直线的距离垂线段最短可知,当BC⊥CD时,BC的值最小,
∵C点的横坐标与纵坐标互为相反数,
∴点C在直线y=-x上运动,BC⊥直线y=-x,如下图所示:
易求得直线BC的解析式为:y=x-3
C点所在的直线为:y=-x,联立两个一次函数解析式:
,解得 ,故 ,
故答案为:B.
6.【答案】 B
解:如图:
A、如图1,∵∠AEF=120°,∠A=30°,∴∠A'EA=2∠AFE=60°=∠B,∴FA'∥BC,
不符合题意;
B、如图2,无法推得两三角形有一组边平行,符合题意;
C、如图3,∵∠A'EC=180°-2∠AEF=180°-150°=30°=∠A‘,∴A'F∥CA,不符合题意;
D、∠AEA'=2∠AEF=2×45°=90°=∠C,∴A'E∥BC,不符合题意;
故答案为:B.
二、填空题
7.【答案】 AD=BC(答案不唯一)
解:根据一组对边平行且相等的四边形是平行四边形,可以添加条件AD=BC,
根据两组对边分别平行的四边形是平行四边形,可以添加条件AB∥DC,
本题只需添加一个即可,
故答案为:AD=BC(答案不唯一).
8.【答案】 -4
解:连接OA
∵AB⊥y,BC∥AD
∴四边形ABCD为平行四边形
∵平行四边形ABCDA的面积为4,即AB×OB=4
∴S△AOB=AB×OB=2=|k|
∴k=-4或k=4(舍去) 21·cn·jy·com
9.【答案】 16
解:∵DE∥AB,DF∥AC,
则四边形AFDE是平行四边形,
∠B=∠EDC,∠FDB=∠C
∵AB=AC,
∴∠B=∠C,
∴∠B=∠FDB,∠C=∠EDF
∴BF=FD,DE=EC,
所以:?AFDE的周长等于AB+AC=16.
故答案为:16.
10.【答案】 (4,3)
解:过点A作AH⊥x轴于点H,
∵A(1,3),
∴AH=3,
由平移得AB∥CD,AB=CD,
∴四边形ABDC是平行四边形,
∴AC=BD,
∵ ,
∴BD=3,
∴AC=3,
∴C(4,3)
故答案为:(4,3).
三、综合题
11.【答案】 (1)解:符合条件的平行四边形如图1、2所示.(答案不唯一)
(2)6
解:_è§???????2??????_1中所画的平行四边形的面积=3×2=6.
故答案为:6.
12.【答案_???_è§???????C_M是直角三角形的斜边上的中线,
∴CM=AM,
∴∠MAC=∠ACM,
∵AM=AN,
∴∠AMN=∠ANM,
∵MN//AC,
∴∠MAC=∠AMN,
∴∠MAC=∠ACM=∠AMN=∠ANM,
∴∠AMC=∠MAN,
∴AN//CM
∴四边形ACMN是平行四边形,
∴MN=AC. 21*cnjy*com
13.【答案】 (1)证明:∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCG=∠EDG,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
∴△FCG≌△EDG(ASA)
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)3.5
解:(2)当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M ,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM ,
在△MBA和△EDC中,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5.
14.【答案】 (1)证明:∵点D,E分别是边AB,AC的中点,
∴DE∥BC.
∵CF∥AB,
∴四边形BCFD是平行四边形;
(2)解:∵AB=BC,E为AC的中点,
∴BE⊥AC.
∴
∵AB=2DB=4,BE=3,
15.【答案】 (1)证明:∵∠ACB=90°,E是BA的中点,∴CE=AE,∵AF=AE,∴AF=CE,
∵ED平分∠BEC,∴∠1=∠2,∵AF=AE,∴∠F=∠3,∵∠1=∠3,
∴∠2=∠F,∴CE∥AF,又∵CE=AF,∴四边形ACEF是平行四边形
(2)解:△AFE △AEC △HDC △CFB
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第18章 18.2 平行四边形的判定
一、单选题
1.下列命题中,正确的个数有(?? )
①若 ,则a、b中至少有一个是0.
②若S△ABC=S△ABD(C、D不重合),则CD∥AB。
③图象为直线的函数的解析式为一次函数。
④有一组对边相等和一组对角相等的四边形是平行四边形。
A.?0个??????????????????????????????????????B.?1个??????????????????????????????????????C.?2个??????????????????????????????????????D.?4 个
2.下列命题中,正确的是(??? )
A.?在三角形中,到三角形_???è??è·??????????_的点是三条边垂直平分线的交点???
B.?平行四边形是轴对称图形???
C.?三角形的中位线将三角形分成面积相等的两个部分???
D.?一组对边平行,一组对角相等的四边形是平行四边形21教育网
3.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为 、 、 ,若 =3, =8,则 的值为(?? ) 21·世纪*教育网
A.?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?44?????????????????????????????????????????D.?48
4.一个零件的形状如图所示, ,则 的度数是(?? )
A.?70°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
5.如图,在平面直角坐标系中,点 ,当四边形 ABCD 的周长最小时,则 m 的值为(?? ). www-2-1-cnjy-com
A.???????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?3
6.如图,△ABC中,∠_B???90?°???_∠A=30°,E,F分别是边AB,AC上的点,连结EF,将△AEF沿着者EF折叠,得到△A'EF,当△A'EF的三边与△ABC的三边有一组边平行时,∠AEF的度数不可能是(?? )
A.?120°?????????????????????????????????????B.?105°?????????????????????????????????????C.?75°?????????????????????????????????????D.?45°
二、填空题
7.如图,在四_è?????ABCD_中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件________,使四边形ABCD是平行四边形(填一个即可). 【来源:21cnj*y.co*m】
8.如图,点A是反比例函数y= 图像上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为4,则k=________?。 2·1·c·n·j·y
9.如图,在 中, ,D是BC上的任一点, 交AC于点E, 交AB于点F那么四边形AFDE的周长是________. 21教育名师原创作品
10.如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为________. 21*cnjy*com
三、综合题
11.如图都是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点.
(1)请在如图1,如图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等).
(2)如图1中所画的平行四边形的面积为________.
12.如图,在 ABC中, ,M是斜边AB的中点,AM=AN, .求证:MN=AC.
13.如图,平行四边形ABCD中_???AB???3c_m , BC=5cm , ∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F , 连结CE , DF .
(1)求证:四边形CEDF是平行四边形;
(2)当AE=________cm时,四边形CEDF是矩形.(直接写出答案,不需要说明理由)
14.如图, 中,点 , 分别是边 , 的中点,过点 作 交 的延长线于点 ,连结 .
(1)求证:四边形 是平行四边形.
(2)当 时,若 , ,求 的长.
15.如图1,△ABC中,∠ACB=90°,E是AB的中点, ED平分∠BEC交BC于点D,F在DE延长线上且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)如图2若四边形ACE_F???è?±??????è??_接FC,BF,FC与AB交于点H,连接DH,在不添加任何辅助线的情况下,请写出图2中的所有等边三角形
答案解析部分
一、单选题
1.【答案】 B
解: ①若 ,则a、b中至少有一个是0,故①正确;
②若S△ABC=S△ABD(C、D不重合),当点C,D在AB的同一侧时,CD∥AB,当点C,D在AB的两侧时,AB不平行CD,故②错误;
③图象为直线的函数的解析式不一定为一次函数,比如直线x=2或直线y=5,它们不是一次函数,故③错误;
④有一组对边相等和一组对角相等的四边形不一定是平行四边形。故 ④错误;
正确的个数为1个.
故答案为:B.
2.【答案】 D
解:A、在三角_???????????°???è§?_形三边距离相等的点是三条角平分线的交点 ,故A不符合题意;
B、 平行四边形是中心对称图形,不是轴对称图形,故B不符合题意;
C、 三角形的中线将三角形分成面积相等的两个部分 ,故C不符合题意;
D、 一组对边平行,一组对角相等的四边形是平行四边形,故D符合题意. 21世纪教育网版权所有
故答案为:D.
3.【答案】 C
解:∵S1=3,S3=8
∴AB= ,CD=
过A作AE∥CD交BC于E
则∠AEB=∠DCB
∵AD∥BC
∴四边形AECD是平行四边形
∴CE=AD,AE=CD=
∵∠ABC+∠DCB=90°
∴∠AEB+∠ABC=90°
∴∠BAE=90°
∴BE=
∵BC=2AD
∴BC=2BE=
∴S2=
故答案为:C.
4.【答案】 B
解:延长DE与BC交于点F,如图:
∵ ,
∴四边形ABFD是平行四边形,
∴∠A=∠F,
在△BDF中, ,
∴ ,
∴∠A=80°;
故答案为:B.
5.【答案】 B
解:∵A(1,5),B(4,1),C(m,-m),D(m-3,-m+4),
∴ , ,
∴AB=CD,
∵点B向左平移3个单位,再向上平移4个单位得到A,点C向左平移3个单位,再向上平移4个单位得到D,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BC=AD,
故四边形ABCD的周长为2(AB+BC),而AB=5,故只要BC最短,则周长最短,
∴由点到直线的距离垂线段最短可知,当BC⊥CD时,BC的值最小,
∵C点的横坐标与纵坐标互为相反数,
∴点C在直线y=-x上运动,BC⊥直线y=-x,如下图所示:
易求得直线BC的解析式为:y=x-3
C点所在的直线为:y=-x,联立两个一次函数解析式:
,解得 ,故 ,
故答案为:B.
6.【答案】 B
解:如图:
A、如图1,∵∠AEF=120°,∠A=30°,∴∠A'EA=2∠AFE=60°=∠B,∴FA'∥BC,
不符合题意;
B、如图2,无法推得两三角形有一组边平行,符合题意;
C、如图3,∵∠A'EC=180°-2∠AEF=180°-150°=30°=∠A‘,∴A'F∥CA,不符合题意;
D、∠AEA'=2∠AEF=2×45°=90°=∠C,∴A'E∥BC,不符合题意;
故答案为:B.
二、填空题
7.【答案】 AD=BC(答案不唯一)
解:根据一组对边平行且相等的四边形是平行四边形,可以添加条件AD=BC,
根据两组对边分别平行的四边形是平行四边形,可以添加条件AB∥DC,
本题只需添加一个即可,
故答案为:AD=BC(答案不唯一).
8.【答案】 -4
解:连接OA
∵AB⊥y,BC∥AD
∴四边形ABCD为平行四边形
∵平行四边形ABCDA的面积为4,即AB×OB=4
∴S△AOB=AB×OB=2=|k|
∴k=-4或k=4(舍去) 21·cn·jy·com
9.【答案】 16
解:∵DE∥AB,DF∥AC,
则四边形AFDE是平行四边形,
∠B=∠EDC,∠FDB=∠C
∵AB=AC,
∴∠B=∠C,
∴∠B=∠FDB,∠C=∠EDF
∴BF=FD,DE=EC,
所以:?AFDE的周长等于AB+AC=16.
故答案为:16.
10.【答案】 (4,3)
解:过点A作AH⊥x轴于点H,
∵A(1,3),
∴AH=3,
由平移得AB∥CD,AB=CD,
∴四边形ABDC是平行四边形,
∴AC=BD,
∵ ,
∴BD=3,
∴AC=3,
∴C(4,3)
故答案为:(4,3).
三、综合题
11.【答案】 (1)解:符合条件的平行四边形如图1、2所示.(答案不唯一)
(2)6
解:_è§???????2??????_1中所画的平行四边形的面积=3×2=6.
故答案为:6.
12.【答案_???_è§???????C_M是直角三角形的斜边上的中线,
∴CM=AM,
∴∠MAC=∠ACM,
∵AM=AN,
∴∠AMN=∠ANM,
∵MN//AC,
∴∠MAC=∠AMN,
∴∠MAC=∠ACM=∠AMN=∠ANM,
∴∠AMC=∠MAN,
∴AN//CM
∴四边形ACMN是平行四边形,
∴MN=AC. 21*cnjy*com
13.【答案】 (1)证明:∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCG=∠EDG,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
∴△FCG≌△EDG(ASA)
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)3.5
解:(2)当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M ,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM ,
在△MBA和△EDC中,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5.
14.【答案】 (1)证明:∵点D,E分别是边AB,AC的中点,
∴DE∥BC.
∵CF∥AB,
∴四边形BCFD是平行四边形;
(2)解:∵AB=BC,E为AC的中点,
∴BE⊥AC.
∴
∵AB=2DB=4,BE=3,
15.【答案】 (1)证明:∵∠ACB=90°,E是BA的中点,∴CE=AE,∵AF=AE,∴AF=CE,
∵ED平分∠BEC,∴∠1=∠2,∵AF=AE,∴∠F=∠3,∵∠1=∠3,
∴∠2=∠F,∴CE∥AF,又∵CE=AF,∴四边形ACEF是平行四边形
(2)解:△AFE △AEC △HDC △CFB
_21?????????è?????(www.21cnjy.com)_
