19.3 正方形 同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第19章 19.3 正方形
一、单选题
1.下列说法正确的是(??? )
A.?有一个角是直角的平行四边形是正方形???????????????B.?对角线互相垂直的矩形是正方形
C.?有一组邻边相等的菱形是正方形?????????????????????????D.?各边都相等的四边形是正方形
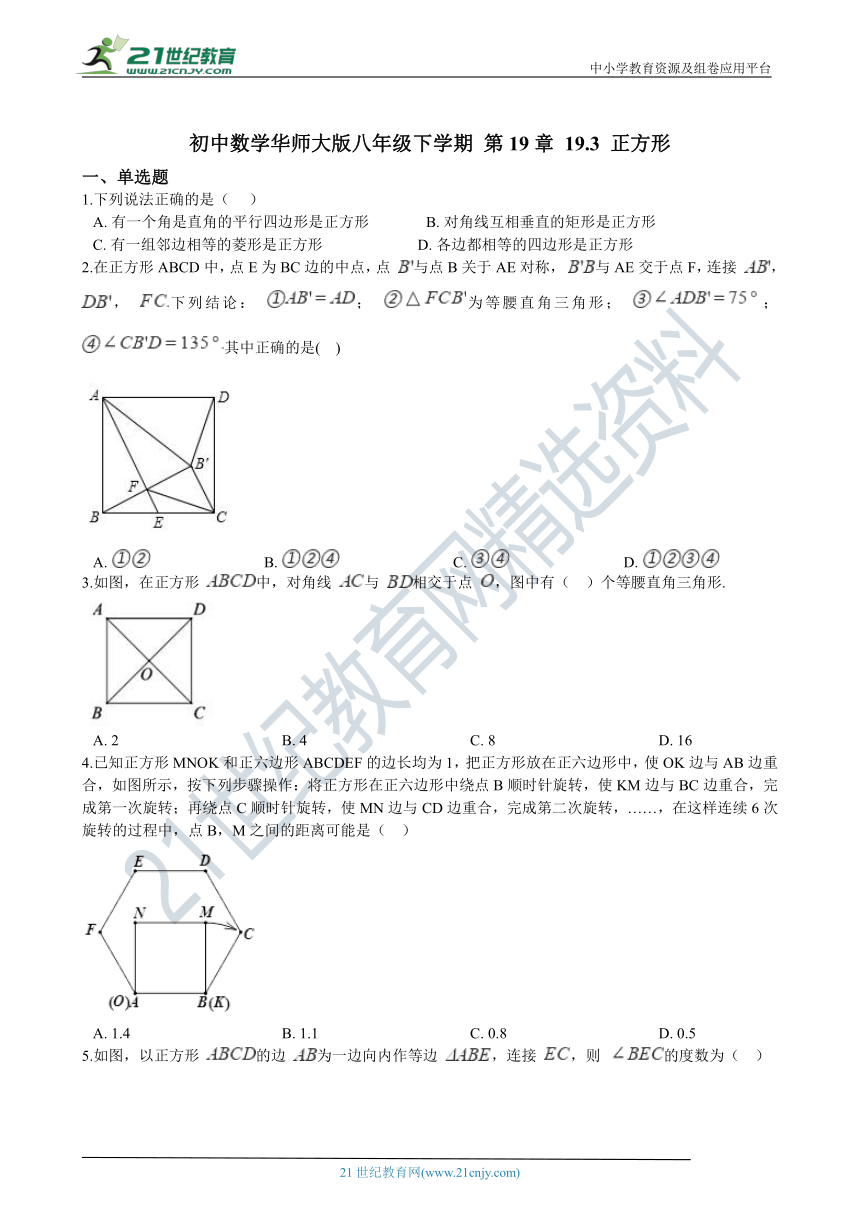
2.在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称, 与AE交于点F,连接 , , 下列结论: ; 为等腰直角三角形; ; 其中正确的是(?? ) 2·1·c·n·j·y
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,在正方形 中,对角线 与 相交于点 ,图中有(?? )个等腰直角三角形.
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?8???????????????????????????????????????????D.?16
4.已知正方形MNOK_?????????è?????A_BCDEF的边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转,……,在这样连续6次旋转的过程中,点B,M之间的距离可能是(?? ) 21·世纪*教育网
A.?1.4????????????????????????????????????????B.?1.1????????????????????????????????????????C.?0.8????????????????????????????????????????D.?0.5
5.如图,以正方形 的边 为一边向内作等边 ,连接 ,则 的度数为(?? )
A.?60°??????????????????????????????????????B.?45°??????????????????????????????????????C.?75°??????????????????????????????????????D.?67.5°
6.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如利用图1可以得到 ,那么利用图2所得到的数学等式是(??? ) www-2-1-cnjy-com
A.????????????????????????????????????B.?
C.?????????????D.?2-1-c-n-j-y
7.如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为(?? ). 21*cnjy*com
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
8.已知在四边形ABCD中, ,若使四边形ABCD是正方形,则还需加上一个条件:________. 【出处:21教育名师】
9.正方形的对角线长为2,则正方形的边长为________cm.面积为________cm2. 21教育名师原创作品
10.如图,正方形ABCO的边长为1,CO、AO分别在x轴、y轴上,将正方形ABCO绕点O逆时针旋转 ,旋转后点B对应的点的坐标为________. 21*cnjy*com
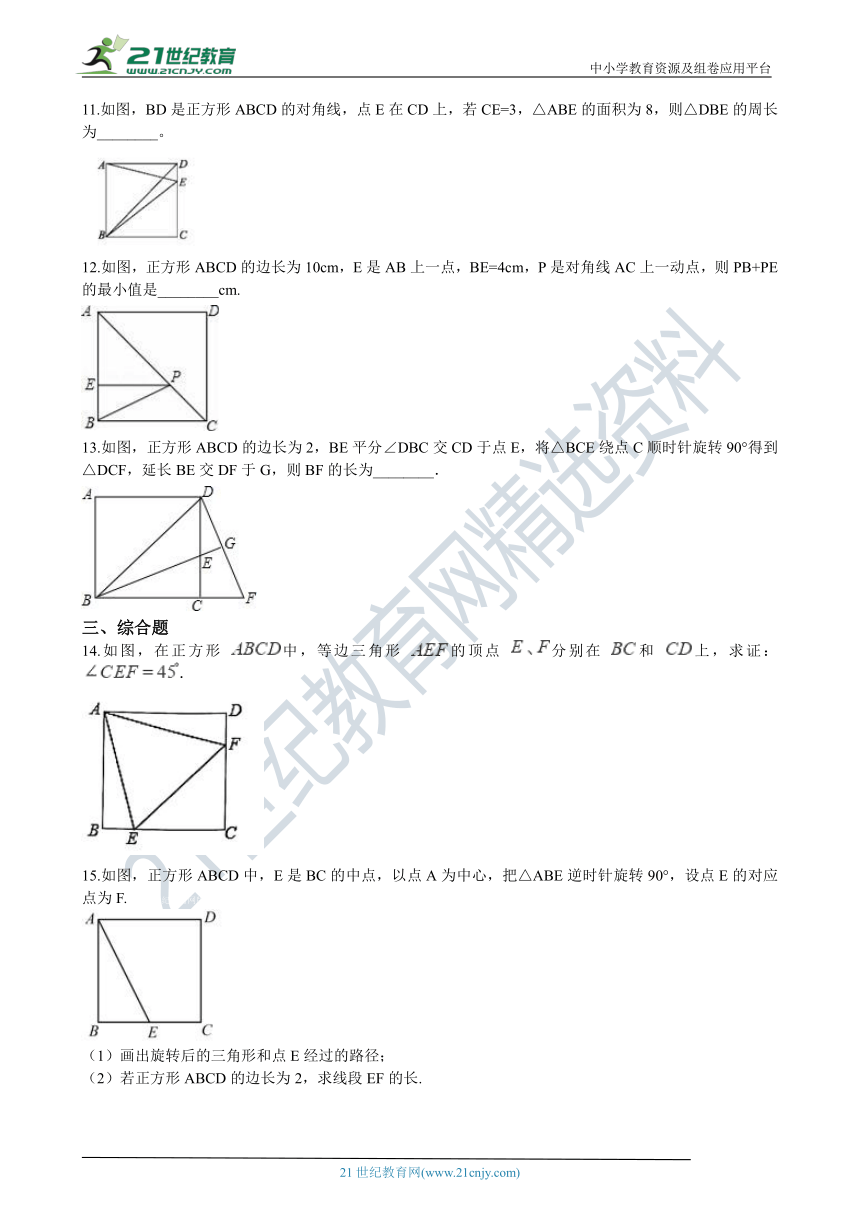
11.如图,BD是正方形ABCD的对角线,点E在CD上,若CE=3,△ABE的面积为8,则△DBE的周长为________。
12.如图,正_??????ABCD_的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是________cm.
13.如图,正方形ABCD_???è??é?????2???_BE平分∠DBC交CD于点E,将△BCE绕点C顺时针旋转90°得到△DCF,延长BE交DF于G,则BF的长为________.
三、综合题
14.如图,在正方形 中,等边三角形 的顶点 分别在 和 上,求证: .
15.如图,正方形ABCD中,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F. 21世纪教育网版权所有
(1)画出旋转后的三角形和点E经过的路径;
(2)若正方形ABCD的边长为2,求线段EF的长.
16.已知,如_????????????AB_CD中,AD=6,DC=7,菱形EFGH的三个顶点E , G , H分别在矩形ABCD的边AB , CD , AD上,AH=2,连接CF .
(1)当四边形EFGH为正方形时,求DG的长;
(2)当DG=6时,求△FCG的面积;
(3)求△FCG的面积的最小值.
答案解析部分
一、单选题
1.【答案】 B
解:A.有一个角是直角的平行四边形是正方形,说法错误,应是矩形,不符合题意;
B.对角线互相垂直的矩形是正方形,符合题意;
C.一组邻边相等的矩形是正方形,不合题意;
D.各边都相等的四边形是菱形,不是正方形,不合题意.
故答案为:B.
2.【答案】 B
解: 点 与点B关于AE对称,
与 关于AE对称,
,
,
故 正确; 如图,连接 .
则 ,
,
.
则 ,
即 为直角三角形.
为 的中位线,
,
∽ ,
,
即 ,
故FB .
.
为等腰直角三角形.
故 正确. 设 度,
度,
则在四边形 中, ,
即 度.
又 ,
.
故 正确. 假设 成立,
则 ,
,
为等边三角形,
故B ,与 矛盾,
故 错误.
故答案为:B.
3.【答案】 C
解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA ,OA=OC=OD=OB,
∠BAD=∠ABC=∠BCD=∠CDA=90°,∠AOB=∠BOC=∠COD=∠DOA=90°.
∴图中等腰直角三角形有:△ABO、△BCO、△CDO、△DAO、△ABC、△ADC、△ABD、△BCD,共8个.
故答案为:C.
4.【答案】 C
解:如图,在这样连续6次旋转过程中,点M的运动轨迹是图中的红线,
观察图形可知点B、M之间的大于2-而小于等于1,
故答案为:C.
5.【答案】 C
解:在正方形 中, .
是等边三角形,
,
,
,
故答案为:C.
6.【答案】 B
解:∵正方形的面积=(a+b+c)2 , 正方形的面积=a2+b2+c2+2ab+2ac+2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:B.
7.【答案】 C
解:连接 、 、 关于 AC 对称.
∴ .
∴ ,当 、 、 三点共线得 最小.
∴ ,选C.
二、填空题
8.【答案】 (答案不唯一)
解:四边形ABCD中, ,使得四边形ABCD是正方形还需加上一个 条件.理由如下:
,
四边形ABCD是矩形,
又 ,
矩形ABCD是正方形.
故答案为: 答案不唯一 .
9.【答案】 ;2
解:如图,正方形ABCD中,对角线AC=2,
由正方形的性质可知△ABC为等腰直角三角形,
∴AB=BC, ,
∴ ,S正方形=AB2=2,
故答案为: ;2.
10.【答案】
解:将正方形ABCO绕点O逆时针旋转 ,设旋转后点B对应的点为D,连接OB,
四边形ABCO是正方形, ,
, ,
点D在y轴上, ,
点D的坐标为 ,
则旋转后点B对应的点的坐标为
故答案为:
11.【答案】 4 +6
解:∵四边形ABCD是正方形,
∴AB=BC=CD,∠C=∠BAD=90°,
∵ △ABE的面积为8,
∴,
∴AB=BC=CD=4,
∴BD=,
∵ CE=3,
∴BE=, DE=1,
∴ △DBE的周长=BD+BE+DE=.
故答案为:
12.【答案】
解:_è???????????????°?_军饮马“类型的两条线段之和的最小值问题,可作点E关于AC的对称点F,连接BF,则BF的长就是PE+PF的最小值.
如图,在AD取一点F,使AF=AE,连接BF,则BF的长就是PE+PF的最小值,
在Rt△ABF中,AB=10,AF=AE=10-4=6,由勾股定理得:
.
故答案为 .
13.【答案】 2
解:过点E作EM⊥BD于点M , 如图所示.
∵四边形ABCD为正方形,
∴∠BDC=45°,∠BCD=90°,
∴△DEM为等腰直角三角形.
∴EM= DE ,
∵BE平分∠DBC , EM⊥BD ,
∴EM=EC ,
设EM=EC=x ,
∵CD=2,
∴DE=2﹣x ,
∴x= (2﹣x),
解得x=2 ﹣2,
∴EM=2 ﹣2,
由旋转的性质可知:CF=CE=2 ﹣2,
∴BF=BC+CF=2+2 ﹣2=2 .
故答案为:2 .
三、综合题
14.【答案】 证明:∵在正方形 中:
, ,
在等边三角形 中: ,
∴ ,
∴
∴
∴
∴ 是等腰直角三角形,
∴∠CEF=45°.
15.【答案】 (1)解:旋转后的△ADF如图所示,点E的运动路径如图所示:
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,∠B=90°,
∵BE=EC=1,
∴AE= = = ,
∵△EAF是等腰直角三角形,∠EAF=90°,AE=AF,
∴EF= AE= .
16.【答案】 (1)解:∵四边形EFGH为正方形,
∴HG=HE,∠EAH=∠D=90°,
∵∠DHG+∠AHE=90°,
∠DHG+∠DGH=90°,
∴∠DGH=∠AHE,
∴△AHE≌△DGH(AAS),
∴DG=AH=2;
(2)解:过F作FM⊥DC,交DC延长线于M,连接GE,
∵AB∥CD,
∴∠AEG=∠MGE,
∵HE∥GF,
∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG(AAS),
∴FM=HA=2,
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,
因此S△FCG= ×FM×GC= ×2×(7-6)=1;
(3)解:设DG=x,则由(2)得,S△FCG=7-x,
在△AHE中,AE≤AB=7,
∴HE2≤53,
∴x2+16≤53,
∴x≤ ,
∴S△FCG的最小值为7- ,此时DG= ,
∴当DG= 时,△FCG的面积最小为(7- ).
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第19章 19.3 正方形
一、单选题
1.下列说法正确的是(??? )
A.?有一个角是直角的平行四边形是正方形???????????????B.?对角线互相垂直的矩形是正方形
C.?有一组邻边相等的菱形是正方形?????????????????????????D.?各边都相等的四边形是正方形
2.在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称, 与AE交于点F,连接 , , 下列结论: ; 为等腰直角三角形; ; 其中正确的是(?? ) 2·1·c·n·j·y
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,在正方形 中,对角线 与 相交于点 ,图中有(?? )个等腰直角三角形.
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?8???????????????????????????????????????????D.?16
4.已知正方形MNOK_?????????è?????A_BCDEF的边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转,……,在这样连续6次旋转的过程中,点B,M之间的距离可能是(?? ) 21·世纪*教育网
A.?1.4????????????????????????????????????????B.?1.1????????????????????????????????????????C.?0.8????????????????????????????????????????D.?0.5
5.如图,以正方形 的边 为一边向内作等边 ,连接 ,则 的度数为(?? )
A.?60°??????????????????????????????????????B.?45°??????????????????????????????????????C.?75°??????????????????????????????????????D.?67.5°
6.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如利用图1可以得到 ,那么利用图2所得到的数学等式是(??? ) www-2-1-cnjy-com
A.????????????????????????????????????B.?
C.?????????????D.?2-1-c-n-j-y
7.如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为(?? ). 21*cnjy*com
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
8.已知在四边形ABCD中, ,若使四边形ABCD是正方形,则还需加上一个条件:________. 【出处:21教育名师】
9.正方形的对角线长为2,则正方形的边长为________cm.面积为________cm2. 21教育名师原创作品
10.如图,正方形ABCO的边长为1,CO、AO分别在x轴、y轴上,将正方形ABCO绕点O逆时针旋转 ,旋转后点B对应的点的坐标为________. 21*cnjy*com
11.如图,BD是正方形ABCD的对角线,点E在CD上,若CE=3,△ABE的面积为8,则△DBE的周长为________。
12.如图,正_??????ABCD_的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是________cm.
13.如图,正方形ABCD_???è??é?????2???_BE平分∠DBC交CD于点E,将△BCE绕点C顺时针旋转90°得到△DCF,延长BE交DF于G,则BF的长为________.
三、综合题
14.如图,在正方形 中,等边三角形 的顶点 分别在 和 上,求证: .
15.如图,正方形ABCD中,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F. 21世纪教育网版权所有
(1)画出旋转后的三角形和点E经过的路径;
(2)若正方形ABCD的边长为2,求线段EF的长.
16.已知,如_????????????AB_CD中,AD=6,DC=7,菱形EFGH的三个顶点E , G , H分别在矩形ABCD的边AB , CD , AD上,AH=2,连接CF .
(1)当四边形EFGH为正方形时,求DG的长;
(2)当DG=6时,求△FCG的面积;
(3)求△FCG的面积的最小值.
答案解析部分
一、单选题
1.【答案】 B
解:A.有一个角是直角的平行四边形是正方形,说法错误,应是矩形,不符合题意;
B.对角线互相垂直的矩形是正方形,符合题意;
C.一组邻边相等的矩形是正方形,不合题意;
D.各边都相等的四边形是菱形,不是正方形,不合题意.
故答案为:B.
2.【答案】 B
解: 点 与点B关于AE对称,
与 关于AE对称,
,
,
故 正确; 如图,连接 .
则 ,
,
.
则 ,
即 为直角三角形.
为 的中位线,
,
∽ ,
,
即 ,
故FB .
.
为等腰直角三角形.
故 正确. 设 度,
度,
则在四边形 中, ,
即 度.
又 ,
.
故 正确. 假设 成立,
则 ,
,
为等边三角形,
故B ,与 矛盾,
故 错误.
故答案为:B.
3.【答案】 C
解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA ,OA=OC=OD=OB,
∠BAD=∠ABC=∠BCD=∠CDA=90°,∠AOB=∠BOC=∠COD=∠DOA=90°.
∴图中等腰直角三角形有:△ABO、△BCO、△CDO、△DAO、△ABC、△ADC、△ABD、△BCD,共8个.
故答案为:C.
4.【答案】 C
解:如图,在这样连续6次旋转过程中,点M的运动轨迹是图中的红线,
观察图形可知点B、M之间的大于2-而小于等于1,
故答案为:C.
5.【答案】 C
解:在正方形 中, .
是等边三角形,
,
,
,
故答案为:C.
6.【答案】 B
解:∵正方形的面积=(a+b+c)2 , 正方形的面积=a2+b2+c2+2ab+2ac+2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:B.
7.【答案】 C
解:连接 、 、 关于 AC 对称.
∴ .
∴ ,当 、 、 三点共线得 最小.
∴ ,选C.
二、填空题
8.【答案】 (答案不唯一)
解:四边形ABCD中, ,使得四边形ABCD是正方形还需加上一个 条件.理由如下:
,
四边形ABCD是矩形,
又 ,
矩形ABCD是正方形.
故答案为: 答案不唯一 .
9.【答案】 ;2
解:如图,正方形ABCD中,对角线AC=2,
由正方形的性质可知△ABC为等腰直角三角形,
∴AB=BC, ,
∴ ,S正方形=AB2=2,
故答案为: ;2.
10.【答案】
解:将正方形ABCO绕点O逆时针旋转 ,设旋转后点B对应的点为D,连接OB,
四边形ABCO是正方形, ,
, ,
点D在y轴上, ,
点D的坐标为 ,
则旋转后点B对应的点的坐标为
故答案为:
11.【答案】 4 +6
解:∵四边形ABCD是正方形,
∴AB=BC=CD,∠C=∠BAD=90°,
∵ △ABE的面积为8,
∴,
∴AB=BC=CD=4,
∴BD=,
∵ CE=3,
∴BE=, DE=1,
∴ △DBE的周长=BD+BE+DE=.
故答案为:
12.【答案】
解:_è???????????????°?_军饮马“类型的两条线段之和的最小值问题,可作点E关于AC的对称点F,连接BF,则BF的长就是PE+PF的最小值.
如图,在AD取一点F,使AF=AE,连接BF,则BF的长就是PE+PF的最小值,
在Rt△ABF中,AB=10,AF=AE=10-4=6,由勾股定理得:
.
故答案为 .
13.【答案】 2
解:过点E作EM⊥BD于点M , 如图所示.
∵四边形ABCD为正方形,
∴∠BDC=45°,∠BCD=90°,
∴△DEM为等腰直角三角形.
∴EM= DE ,
∵BE平分∠DBC , EM⊥BD ,
∴EM=EC ,
设EM=EC=x ,
∵CD=2,
∴DE=2﹣x ,
∴x= (2﹣x),
解得x=2 ﹣2,
∴EM=2 ﹣2,
由旋转的性质可知:CF=CE=2 ﹣2,
∴BF=BC+CF=2+2 ﹣2=2 .
故答案为:2 .
三、综合题
14.【答案】 证明:∵在正方形 中:
, ,
在等边三角形 中: ,
∴ ,
∴
∴
∴
∴ 是等腰直角三角形,
∴∠CEF=45°.
15.【答案】 (1)解:旋转后的△ADF如图所示,点E的运动路径如图所示:
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,∠B=90°,
∵BE=EC=1,
∴AE= = = ,
∵△EAF是等腰直角三角形,∠EAF=90°,AE=AF,
∴EF= AE= .
16.【答案】 (1)解:∵四边形EFGH为正方形,
∴HG=HE,∠EAH=∠D=90°,
∵∠DHG+∠AHE=90°,
∠DHG+∠DGH=90°,
∴∠DGH=∠AHE,
∴△AHE≌△DGH(AAS),
∴DG=AH=2;
(2)解:过F作FM⊥DC,交DC延长线于M,连接GE,
∵AB∥CD,
∴∠AEG=∠MGE,
∵HE∥GF,
∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG(AAS),
∴FM=HA=2,
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,
因此S△FCG= ×FM×GC= ×2×(7-6)=1;
(3)解:设DG=x,则由(2)得,S△FCG=7-x,
在△AHE中,AE≤AB=7,
∴HE2≤53,
∴x2+16≤53,
∴x≤ ,
∴S△FCG的最小值为7- ,此时DG= ,
∴当DG= 时,△FCG的面积最小为(7- ).
_21?????????è?????(www.21cnjy.com)_
