19.1矩形 同步练习(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第19章 19.1矩形
一、单选题
1.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是矩形,还需添加一个条件,这个条件可以是( ??) www.21-cn-jy.com
A.?AO=CO?????????????????????????B.?AO=BO?????????????????????????C.?AO⊥BO?????????????????????????D.?∠OBC=∠OBA
2.如图, 是一个中心对称图形的一部分,O点是对称中心,点A和点B是一对对应点, ,那么将这个图形补成一个完整的图形是( ) www-2-1-cnjy-com
A.?矩形????????????????????????????????????B.?菱形????????????????????????????????????C.?正方形????????????????????????????????????D.?梯形
3.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是(?? )
A.???????????????????????????????????????B.?3 ??????????????????????????????????????C.???????????????????????????????????????D.?5
4.如图,在矩形 中,两条对角线 与 相交于点 , , ,则 的长为(?? )
A.?5???????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
5.如图,长方形ABCD是由6个正方形组成,其中有两个一样大的正方形,且最小正方形边长为1,则长方形ABCD的边长DC为(?? ?)
21·世纪*教育网
A.?10?????????????????????????????????????????B.?13?????????????????????????????????????????C.?16?????????????????????????????????????????D.?19
6.如图 ,阴影部分是一个长方形,则长方形的面积是(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
7.如图所示,四边形ABCD的对角线为AC,BD,且 ,则下列条件能判定四边形ABCD是矩形的是(?? ) 21*cnjy*com
A.??????????????????????B.?AC,BD互相平分?????????????????????C.??????????????????????D.?
8.如图,点P是Rt△ABC中斜_è??AC_(???_与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( ???)
A.?1.5?????????????????????????????????????????B.?2?????????????????????????????????????????C.?4.8?????????????????????????????????????????D.?2.4
9.如图,?ABCD中,对角线AC,BD相交于点O,OA=3,若要使平行四边形ABCD为矩形,则OB的长度为( ) 21*cnjy*com
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
二、填空题
10.杨师傅要做一个长方形的_???é??????????????_量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面________.(填“合格”或“不合格”). 【来源:21cnj*y.co*m】
11.如图,对折矩形ABCD,使_AB???DCé??_合,得到折痕EF,将纸片展平再一次折叠,使点D落到G,并使折痕经过点A,已知BC=2.则线段EG的长度为________.
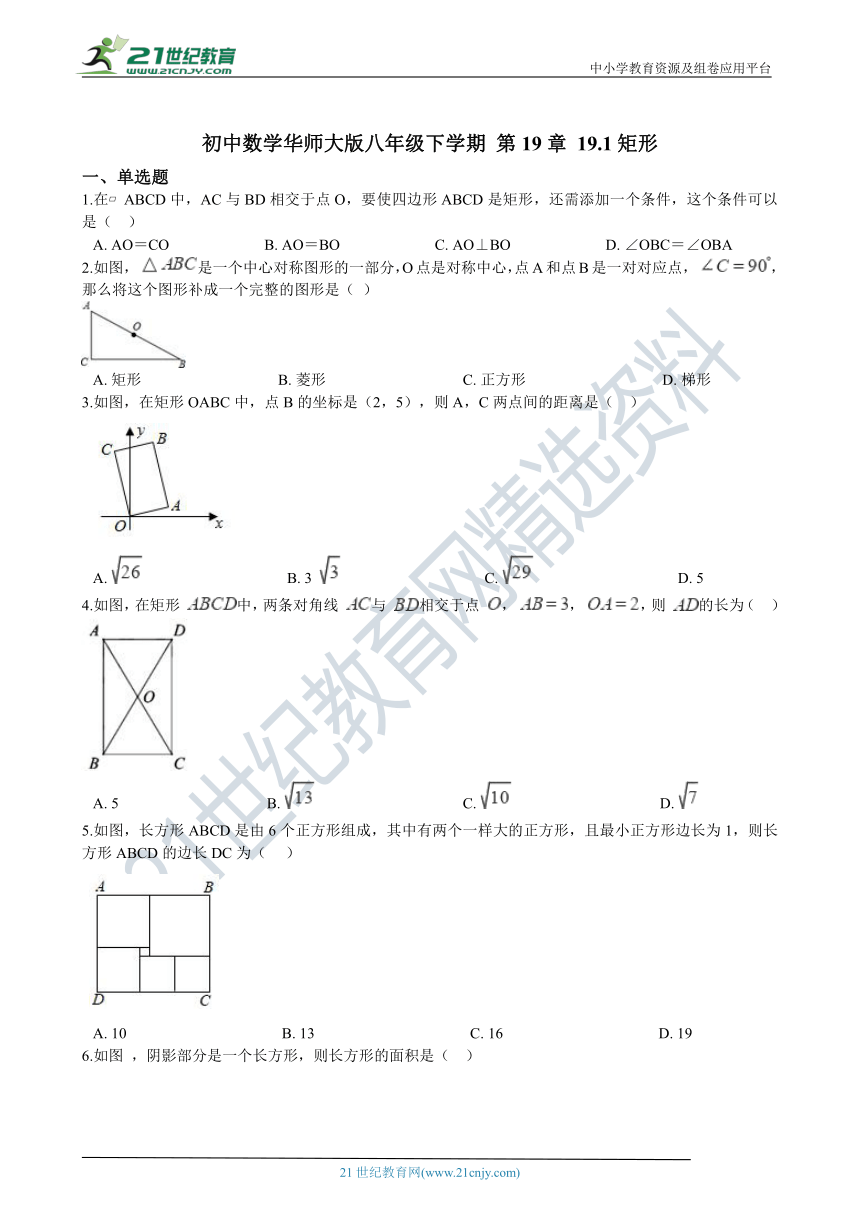
12.如图,有一矩形纸片OAB_C?????¨???è§????_标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为________。
三、综合题
13.如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
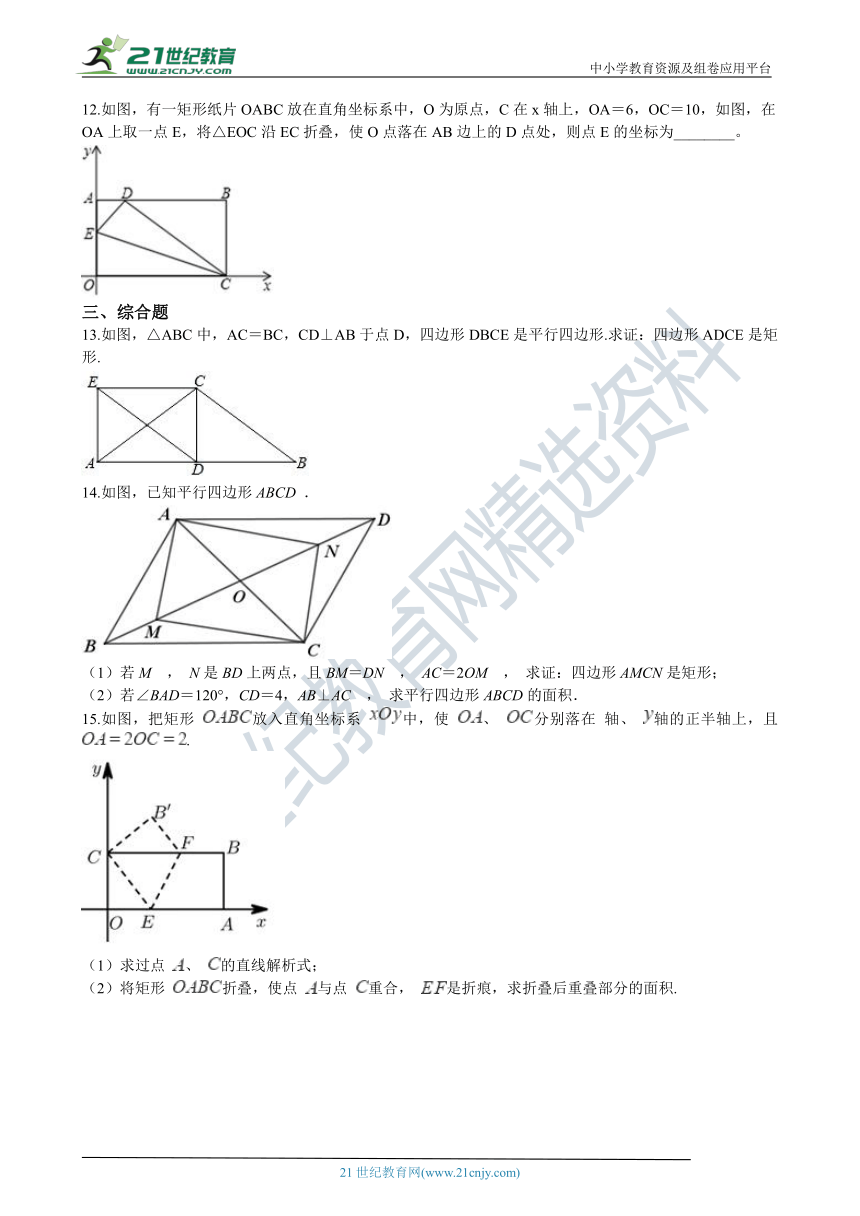
14.如图,已知平行四边形ABCD .
(1)若M , N是BD上两点,且BM=DN , AC=2OM , 求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC , 求平行四边形ABCD的面积.
15.如图,把矩形 放入直角坐标系 中,使 、 分别落在 轴、 轴的正半轴上,且 . 21教育网
(1)求过点 、 的直线解析式;
(2)将矩形 折叠,使点 与点 重合, 是折痕,求折叠后重叠部分的面积.
答案解析部分
一、单选题
1.【答案】 B
解:添加AO=BO ,
理由是:∵四边形ABCD是平行四边形,
∴OA=OC , OB=OD ,
∵OA=OB ,
∴AC=BD ,
∴?ABCD为矩形,
故答案为:B .
2.【答案】 A
解:如图,
∵O点是对称中心,△A′B′C′是△ABC关于点O的对称图形,
∴AC′=BC,BC′=AC,
∴四边形ACBC′是平行四边形,
∵∠C=90°,
∴平行四边形ACBC′是矩形.
故答案为:A.
3.【答案】 C
解:连接OB,AC,
∵点B的坐标为(2,5),
∴BO=.
∵矩形OABC,
∴.
故答案为:C.
4.【答案】 D
解:∵四边形ABCD是矩形,
∴OB=OD=OA=OC,∠BAD= ,
∴BD=2OA=4,
在Rt△ABD中,AD= ,
故答案为:D.
5.【答案】 B
解:
设右下方两个相等的正方形的边长为x,根据题意可知,
x+3+x+2=x+x+x+1
2x+5=3x+1
x=4
∴长方形的长为4+4+4+1=13
长方形的宽为4+3+4=11
∴DC的长度为13 21教育名师原创作品
故答案为:B.
6.【答案】 C
解:在直角三角形中,根据勾股定理可得,阴影部分长方形的长为=5
∴长方形的面积=1×5=5 【出处:21教育名师】
故答案为:C.
7.【答案】 B
解:能判定四边形ABCD是矩形的条件为AC、BD互相平分,
理由如下: 、BD互相平分,
四边形ABCD是平行四边形,
,
?ABCD是矩形,
其它三个条件再加上 均不能判定四边形ABCD是矩形.
故答案为:B.
8.【答案】 C
解:∵ PM⊥AB , PN⊥BC ,
∴∠PMB=∠PNB=∠ABC=90°,
∴四边形PMBN是矩形,
∴MN=BP,
∴当BP⊥AC时,BP的值最小,即MN的值最小,
∵ AB=6,BC=8,
∴AC=10,
∵AB·BC=AC·BP,
∴×6×8=×10×BP,
∴BP=4.8,
∴ MN的最小值是4.8.
故答案为:4.8.
9.【答案】 B
解:假如平行四边形ABCD是矩形,
OA=OC,OB=OD,AC=BD,
∴OA=OB=3.
故答案为:B.
二、填空题
10.【答案】 不合格
解:如图:
∵22+1.52=6.25 2.152 ,
即:AD2+DC2 AC2 ,
∴∠D 90°,
∴四边形ABCD不是矩形,
∴这个桌面不合格.
故答案为:不合格.
11.【答案】
解:如图,
由题意得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=AM,
∴AN=NG,
∴∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=∠4=30°,
∵四边形ABCD为矩形,
∴AE=AD=BC=1,
∴AG=2,
∴EG=,
故答案为:.
12.【答案】
解:由矩形的性质得:
由翻转变换的性质得:
在 中,
则
设 ,则
在 中, ,即
解得
故点E的坐标为 .
故答案为: .
三、综合题
13.【答案】 证明:∵AC=BC,CD⊥AB,
∴∠ADC=90°,AD=BD.
∵在?DBCE中,EC∥BD,EC=BD,
∴EC∥AD,EC=AD.
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴四边形ADCE是矩形.
14.【答案】 (1)解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC= AB=4 ,
∴平行四边形ABCD的面积=AC?AB=4 4=16 .
15.【答案】 (1)解: .A点坐标为(2,0),C坐标为(0,1),
过点 、 的直线解析式为:y=kx+b,
A、C两点坐标代入得 ,
解得 ,
,
(2)解:将矩形 折叠,使点 与点 重合, 是折痕,则∠CEF=∠AEF,
∵BC∥AO,
∴∠CFE=∠AEF,
∴∠CEF=∠CFE,
CE=CF,
设AE=x,则OE=2-x,
在Rt在Rt△OAE C中,由勾股定理 ,
,
解得 ,
过E作EG⊥BC于G,则四边形OEGC为矩形,EG=OC=1,
折叠后重叠部分的面积S= .
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第19章 19.1矩形
一、单选题
1.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是矩形,还需添加一个条件,这个条件可以是( ??) www.21-cn-jy.com
A.?AO=CO?????????????????????????B.?AO=BO?????????????????????????C.?AO⊥BO?????????????????????????D.?∠OBC=∠OBA
2.如图, 是一个中心对称图形的一部分,O点是对称中心,点A和点B是一对对应点, ,那么将这个图形补成一个完整的图形是( ) www-2-1-cnjy-com
A.?矩形????????????????????????????????????B.?菱形????????????????????????????????????C.?正方形????????????????????????????????????D.?梯形
3.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是(?? )
A.???????????????????????????????????????B.?3 ??????????????????????????????????????C.???????????????????????????????????????D.?5
4.如图,在矩形 中,两条对角线 与 相交于点 , , ,则 的长为(?? )
A.?5???????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
5.如图,长方形ABCD是由6个正方形组成,其中有两个一样大的正方形,且最小正方形边长为1,则长方形ABCD的边长DC为(?? ?)
21·世纪*教育网
A.?10?????????????????????????????????????????B.?13?????????????????????????????????????????C.?16?????????????????????????????????????????D.?19
6.如图 ,阴影部分是一个长方形,则长方形的面积是(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
7.如图所示,四边形ABCD的对角线为AC,BD,且 ,则下列条件能判定四边形ABCD是矩形的是(?? ) 21*cnjy*com
A.??????????????????????B.?AC,BD互相平分?????????????????????C.??????????????????????D.?
8.如图,点P是Rt△ABC中斜_è??AC_(???_与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( ???)
A.?1.5?????????????????????????????????????????B.?2?????????????????????????????????????????C.?4.8?????????????????????????????????????????D.?2.4
9.如图,?ABCD中,对角线AC,BD相交于点O,OA=3,若要使平行四边形ABCD为矩形,则OB的长度为( ) 21*cnjy*com
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
二、填空题
10.杨师傅要做一个长方形的_???é??????????????_量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面________.(填“合格”或“不合格”). 【来源:21cnj*y.co*m】
11.如图,对折矩形ABCD,使_AB???DCé??_合,得到折痕EF,将纸片展平再一次折叠,使点D落到G,并使折痕经过点A,已知BC=2.则线段EG的长度为________.
12.如图,有一矩形纸片OAB_C?????¨???è§????_标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为________。
三、综合题
13.如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
14.如图,已知平行四边形ABCD .
(1)若M , N是BD上两点,且BM=DN , AC=2OM , 求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC , 求平行四边形ABCD的面积.
15.如图,把矩形 放入直角坐标系 中,使 、 分别落在 轴、 轴的正半轴上,且 . 21教育网
(1)求过点 、 的直线解析式;
(2)将矩形 折叠,使点 与点 重合, 是折痕,求折叠后重叠部分的面积.
答案解析部分
一、单选题
1.【答案】 B
解:添加AO=BO ,
理由是:∵四边形ABCD是平行四边形,
∴OA=OC , OB=OD ,
∵OA=OB ,
∴AC=BD ,
∴?ABCD为矩形,
故答案为:B .
2.【答案】 A
解:如图,
∵O点是对称中心,△A′B′C′是△ABC关于点O的对称图形,
∴AC′=BC,BC′=AC,
∴四边形ACBC′是平行四边形,
∵∠C=90°,
∴平行四边形ACBC′是矩形.
故答案为:A.
3.【答案】 C
解:连接OB,AC,
∵点B的坐标为(2,5),
∴BO=.
∵矩形OABC,
∴.
故答案为:C.
4.【答案】 D
解:∵四边形ABCD是矩形,
∴OB=OD=OA=OC,∠BAD= ,
∴BD=2OA=4,
在Rt△ABD中,AD= ,
故答案为:D.
5.【答案】 B
解:
设右下方两个相等的正方形的边长为x,根据题意可知,
x+3+x+2=x+x+x+1
2x+5=3x+1
x=4
∴长方形的长为4+4+4+1=13
长方形的宽为4+3+4=11
∴DC的长度为13 21教育名师原创作品
故答案为:B.
6.【答案】 C
解:在直角三角形中,根据勾股定理可得,阴影部分长方形的长为=5
∴长方形的面积=1×5=5 【出处:21教育名师】
故答案为:C.
7.【答案】 B
解:能判定四边形ABCD是矩形的条件为AC、BD互相平分,
理由如下: 、BD互相平分,
四边形ABCD是平行四边形,
,
?ABCD是矩形,
其它三个条件再加上 均不能判定四边形ABCD是矩形.
故答案为:B.
8.【答案】 C
解:∵ PM⊥AB , PN⊥BC ,
∴∠PMB=∠PNB=∠ABC=90°,
∴四边形PMBN是矩形,
∴MN=BP,
∴当BP⊥AC时,BP的值最小,即MN的值最小,
∵ AB=6,BC=8,
∴AC=10,
∵AB·BC=AC·BP,
∴×6×8=×10×BP,
∴BP=4.8,
∴ MN的最小值是4.8.
故答案为:4.8.
9.【答案】 B
解:假如平行四边形ABCD是矩形,
OA=OC,OB=OD,AC=BD,
∴OA=OB=3.
故答案为:B.
二、填空题
10.【答案】 不合格
解:如图:
∵22+1.52=6.25 2.152 ,
即:AD2+DC2 AC2 ,
∴∠D 90°,
∴四边形ABCD不是矩形,
∴这个桌面不合格.
故答案为:不合格.
11.【答案】
解:如图,
由题意得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=AM,
∴AN=NG,
∴∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=∠4=30°,
∵四边形ABCD为矩形,
∴AE=AD=BC=1,
∴AG=2,
∴EG=,
故答案为:.
12.【答案】
解:由矩形的性质得:
由翻转变换的性质得:
在 中,
则
设 ,则
在 中, ,即
解得
故点E的坐标为 .
故答案为: .
三、综合题
13.【答案】 证明:∵AC=BC,CD⊥AB,
∴∠ADC=90°,AD=BD.
∵在?DBCE中,EC∥BD,EC=BD,
∴EC∥AD,EC=AD.
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴四边形ADCE是矩形.
14.【答案】 (1)解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC= AB=4 ,
∴平行四边形ABCD的面积=AC?AB=4 4=16 .
15.【答案】 (1)解: .A点坐标为(2,0),C坐标为(0,1),
过点 、 的直线解析式为:y=kx+b,
A、C两点坐标代入得 ,
解得 ,
,
(2)解:将矩形 折叠,使点 与点 重合, 是折痕,则∠CEF=∠AEF,
∵BC∥AO,
∴∠CFE=∠AEF,
∴∠CEF=∠CFE,
CE=CF,
设AE=x,则OE=2-x,
在Rt在Rt△OAE C中,由勾股定理 ,
,
解得 ,
过E作EG⊥BC于G,则四边形OEGC为矩形,EG=OC=1,
折叠后重叠部分的面积S= .
_21?????????è?????(www.21cnjy.com)_
