19.2 菱形 同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第19章 19.2 菱形
一、单选题
1.矩形具有而菱形不具有的性质是(?? ?)
A.?对边平行且相等??????????????????B.?对角线垂直??????????????????C.?对角线互相平分??????????????????D.?对角线相等
2.已知四边形ABCD是平行四边形,则下列结论中正确的是(?? )
A.?当AB⊥BD时,它是菱形?????????????????????????????????????B.?当AC=BD时,它是正方形
C.?当∠ABC=90°时,它是矩形????????????????????????????????D.?当AB=BC时,它是矩形21教育网
3.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是(?? )
A.?AC⊥BD????????????????????????????B.?BA⊥BD????????????????????????????C.?AB=CD????????????????????????????D.?AD=BC
4.如图,正方形 的边长为1, , 是对角线.将 绕着点 顺时针旋转45°得到 , 交 于点 ,连接 交 于点 ,连接 .则下列结论:
①四边形 是菱形??? ② ??? ③ ??? ④
其中正确的结论是有(? )个
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
5.如图,在菱形ABC_D?????????AB_C=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=(?? ) 21·cn·jy·com
A.?30°?????????????????????????????????B.?70°?????????????????????????????????C.?30°或60°?????????????????????????????????D.?40°或70°
6.如图,菱形ABCD的对角线AC、BD交于点O , AC=8,BD=6,DE⊥AB于点E , 则DE的长为( ???)
A.?4.8?????????????????????????????????????????B.?5?????????????????????????????????????????C.?9.6?????????????????????????????????????????D.?10
7.已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为(??? )
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?1
8.已知一个菱形的边长是5cm,两条对角线长的比是4:3,则这个菱形的面积是(?? ?)
A.?12cm2????????????????????????????????B.?24cm2????????????????????????????????C.?48cm2????????????????????????????????D.?96cm2
9.如图,菱形ABCD_??????AB=2_,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是(?????? ) 【来源:21·世纪·教育·网】
? ?
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
10.如图,小华剪了两条宽为 的纸条,交叉叠放在一起,且它们较小的交角为 ,则它们重叠部分的面积为(? ) www-2-1-cnjy-com
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
11.菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为________cm2.
12.菱形有一个内角为120°,较长的对角线长为6 ,则它的面积为________.
13.如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是________.
14.如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,若 , ,则 ________. 【出处:21教育名师】
三、综合题
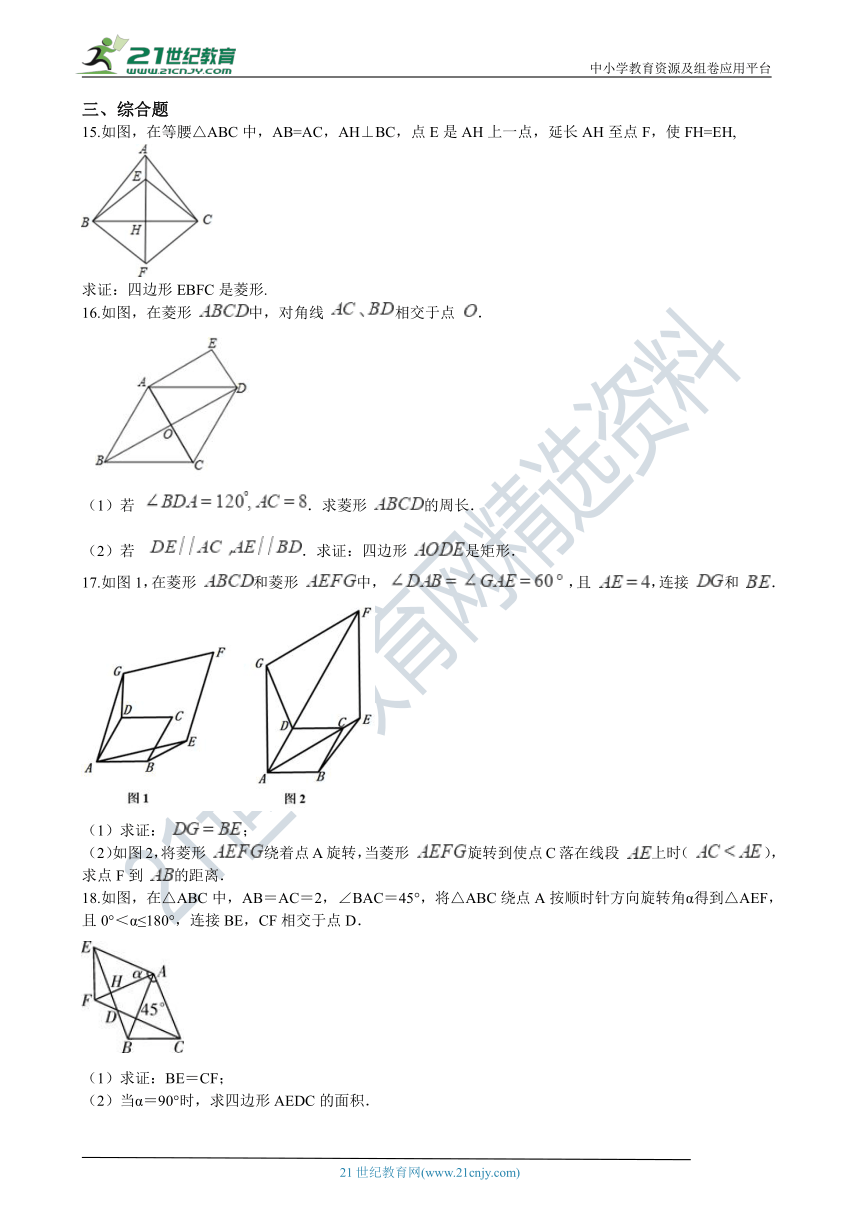
15.如图,在等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH,
求证:四边形EBFC是菱形.
16.如图,在菱形 中,对角线 相交于点 .
(1)若 .求菱形 的周长.
(2)若 .求证:四边形 是矩形.
17.如图1,在菱形 和菱形 中, ,且 ,连接 和 .
(1)求证: ;
(2)如图2,将菱形 绕着点A旋转,当菱形 旋转到使点C落在线段 上时( ),求点F到 的距离. 21教育名师原创作品
18.如图,在△A_BC??????AB_=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE,CF相交于点D. 21*cnjy*com
?
(1)求证:BE=CF;
(2)当α=90°时,求四边形AEDC的面积.
答案解析部分
一、单选题
1.【答案】 D
解:矩形的对角线相等,菱形的对角线互相垂直.
矩形具有而菱形不具有的性质是对角线相等.
故答案为:D.
2.【答案】 C
解:_è§????A????????_AC⊥BD时,四边形ABCD是菱形,故A错误;
B、当AC=BD时,四边形ABCD是矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、 当AB=BC时,四边形ABCD是菱形,故D错误.
故答案为:C.
3.【答案】 A
解:能判定四边形ABCD是菱形的是AC⊥BD,理由如下:
∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:A.
4.【答案】 D
解:证明:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DHG是由△DBC旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在RT△ADE和RT△GDE中,
?
∴Rt△AED≌Rt△GED(HL),故②正确;
∴∠ADE=∠EDG=22.5°,AE=EG,
∴∠AED=∠AFE=67.5°,
∴AE=AF=EG,
又∵∠H=∠DBC=∠DAC=45°,
∴GH∥AC,
∴四边形AEGF是菱形,故①正确;
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=90°+22.5°=112.5°,故③正确;21cnjy.com
∵正方形ABCD的边长为1,
∴∠BCD=∠BAD=90°,∠CBD=45°,BD= ,AD=CD=1.
由旋转的性质可知:∠HGD=BCD=90°,∠H=∠CBD=45°,BD=HD,GD=CD,
∴HA=BG= -1,∠H=∠EBG=45°,∠HAE=∠BGE=90°,
∴△HAE和△BGE均为直角边为 -1的等腰直角三角形,
∴FG=AE= -1 ,故④正确.
综上所述:正确的结论有①②③④.
故答案为:D.
5.【答案】 C
解:∵在菱形ABCD中,∠ABC=80°,
∴∠ABD= ABC=40°,AD∥BC,
∴∠BAD=180°﹣∠ABC=100°,
∵△ABE是等腰三角形,
∴AE=BE,或AB=BE,
当AE=BE时,
∴∠ABE=∠BAE=40°,
∴∠DAE=100°﹣40°=60°;
当AB=BE时,∴∠BAE=∠AEB= (180°﹣40°)=70°,
∴∠DAE=100°﹣70°=30°,
综上所述,当△ABE是等腰三角形时,∠DAE=30°或60°,
故答案为:C.
6.【答案】 A
解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥BD,AO= AC=4,BO= BD=3,
在Rt△AOB中,由勾股定理得:
AB= ,
∵DE⊥AB,
∴S菱形= ·BD·AC=AB·DE,
即 ×6×8=5·DE,
解得:DE= =4.8,
故答案为:A.
7.【答案】 C
解:如图,由题意得:菱形ABCD的周长为8, ,
,
是等边三角形,
,
,
该菱形较短的对角线长为 ,
故答案为:C.
8.【答案】 B
解:如图,
∵四边形ABCD是菱形,
∴OA=OC=AC,OB=OD=BD,AC⊥BD,
∵ 两条对角线长的比是4:3 ,
∴OA:OD=4:3 ,
设OA=4x,OD=3x,
∵OA2+OB2=AB2 ,
∴16x2+9x2=25,
解得x=1,
∴OA=4,OD=3,
∴AC=8,BD=6,
∴S=AC·BD=×8×6=24(cm2).
故答案为:B.
9.【答案】 D
解:连接DE交AC于P,连接BD,BP,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,
∴PE+PB=PE+PD=DE,
即DE就是PE+PB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∴AD=BD,
∵AE=BE=AB=1,
∴DE⊥AB,
在Rt△ADE中,DE=,
∴ PE+PB的最小值是.
故答案为:D.
10.【答案】 D
解:过点D作DE⊥AB,垂足为E;过点D作DF⊥BC,垂足为F. (如图)
根据辅助线作法和纸条宽度的定义可知:∠AED=∠CFD=90°,DE=DF=1,
由纸条的几何特征可知,AD∥BC,AB∥DC,故四边形ABCD为平行四边形,
由题目条件和对顶角关系可知,∠BCD=60°,
∴在平行四边形ABCD中,∠BAD=∠BCD=60°,即∠EAD=∠FCD=60°,
∵在△AED与△CFD中:
,
∴△AED≌△CFD (AAS)
∴AD=CD,
∴平行四边形ABCD为菱形,
∵在Rt△CFD中,∠FCD=60°,
∴∠FDC=30°,
∴在Rt△CFD中, ,
∴在Rt△CFD中, ,
∴ ,
∵在菱形ABCD中,BC=CD,
∴ ,
∴菱形ABCD的面积为: ,即纸片重叠部分的面积为 .
故答案为:D.
二、填空题
11.【答案】 30
解:菱形的面积等于两对角线的积的一半,则这个菱形的面积是6×10× =30cm2.
故答案为:30.
12.【答案】
解:∵菱形ABCD中,∠BAD=120°,
∴∠BAC= ∠BAD=60°,AC⊥BD,
∴∠ABO=30°,
∵BD=6 ,
∴BO=3 ,
设AO=x,则AB=2x,
故x2+(3 )2=(2x)2 ,
解得:x=3,
∴AO=3,
∴AC=6,
∴菱形的面积=6 ×6÷2=18 .
故答案为:18 .
13.【答案】
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC= ×4=2,∠BAC= ∠BAD= ×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB= ,
∴BD=2OB= ,
∴该菱形的面积是: AC?BD= ×4× = ,
故答案为: .
14.【答案】 2.4
解:∵菱形ABCD中,AC=6,BD=8,
∴OA=OC= AC=3,OB= BD=4,AC⊥BD,
∴BC= = =5,
∵S△OBC= ×OC×OB= ×BC×OE,
∴OE= =2.4,
故答案为:2.4.
三、综合题
15.【答案】 证明:∵△ABC为等腰三角形,AH⊥BC,∴H为BC的中点,
又∵FH=EH,∴四边形BECF为平行四边形.
∵AH⊥BC,∴平行四边形BECF为菱形.
16.【答案】 (1)解: 四边形 是菱形,
是等边三角形,
菱形 的周长
(2)证明:
四边形 是平行四边形,
四边形 是菱形
四边形 是矩形
17.【答案】 (1)证明:∵四边形ABCD和四边形AEFG为菱形
∴GA=EA,OA=BA
∵∠DAB=∠GAE=60°
∴∠GAD+∠DAE=60°
∠DAE+∠EAB=60°
∴∠GAD=∠EAB
∴△GAD≌△EAB(SAS)
∴DG=BE
(2)解:延长FE,AB交于点H
∵AC是菱形ABCD对角线
∴∠CAB= ∠DAB=30°
∵∠GAE=60°且四边形AEGF是菱形
∴GA∥FE
∴∠FEA=180°-60°=120°
∴∠AEH=180°-120°=60°
∵∠EAB=30°
∴∠H=90°
∵AE=4,在Rt△EAH=30°
∴EH=2
∴F到AB的距离为4+2=6
18.【答案】 (1)证明:∵将△ABC绕点A按顺时针方向旋转角α得到△AEF,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴AB=AC=AE=AF,∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC.
在△AEB和△AFC中,
∴△AEB≌△AFC(SAS),
∴BE=CF.
(2)解:∵α=90°,
∴∠EAB=∠FAC=90°.
∵AE=AB,
∴△ABE为等腰直角三角形,
∴∠ABE=45°,
∴∠ABE=∠BAC,
∴AC∥BE,
同理可得AE∥CF.
∵AE=AC,
∴四边形AEDC为菱形.
设AF与BE交于点H.
∵∠EAF=45°,
∴AH平分∠EAB,
∴AH⊥BE,
∴△AHE为等腰直角三角形,
∴AH=AE·sin45° AE= ,
∴四边形AEDC的面积为AH·DE= ×2=2 .
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第19章 19.2 菱形
一、单选题
1.矩形具有而菱形不具有的性质是(?? ?)
A.?对边平行且相等??????????????????B.?对角线垂直??????????????????C.?对角线互相平分??????????????????D.?对角线相等
2.已知四边形ABCD是平行四边形,则下列结论中正确的是(?? )
A.?当AB⊥BD时,它是菱形?????????????????????????????????????B.?当AC=BD时,它是正方形
C.?当∠ABC=90°时,它是矩形????????????????????????????????D.?当AB=BC时,它是矩形21教育网
3.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是(?? )
A.?AC⊥BD????????????????????????????B.?BA⊥BD????????????????????????????C.?AB=CD????????????????????????????D.?AD=BC
4.如图,正方形 的边长为1, , 是对角线.将 绕着点 顺时针旋转45°得到 , 交 于点 ,连接 交 于点 ,连接 .则下列结论:
①四边形 是菱形??? ② ??? ③ ??? ④
其中正确的结论是有(? )个
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
5.如图,在菱形ABC_D?????????AB_C=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=(?? ) 21·cn·jy·com
A.?30°?????????????????????????????????B.?70°?????????????????????????????????C.?30°或60°?????????????????????????????????D.?40°或70°
6.如图,菱形ABCD的对角线AC、BD交于点O , AC=8,BD=6,DE⊥AB于点E , 则DE的长为( ???)
A.?4.8?????????????????????????????????????????B.?5?????????????????????????????????????????C.?9.6?????????????????????????????????????????D.?10
7.已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为(??? )
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?1
8.已知一个菱形的边长是5cm,两条对角线长的比是4:3,则这个菱形的面积是(?? ?)
A.?12cm2????????????????????????????????B.?24cm2????????????????????????????????C.?48cm2????????????????????????????????D.?96cm2
9.如图,菱形ABCD_??????AB=2_,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是(?????? ) 【来源:21·世纪·教育·网】
? ?
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
10.如图,小华剪了两条宽为 的纸条,交叉叠放在一起,且它们较小的交角为 ,则它们重叠部分的面积为(? ) www-2-1-cnjy-com
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
11.菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为________cm2.
12.菱形有一个内角为120°,较长的对角线长为6 ,则它的面积为________.
13.如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是________.
14.如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,若 , ,则 ________. 【出处:21教育名师】
三、综合题
15.如图,在等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH,
求证:四边形EBFC是菱形.
16.如图,在菱形 中,对角线 相交于点 .
(1)若 .求菱形 的周长.
(2)若 .求证:四边形 是矩形.
17.如图1,在菱形 和菱形 中, ,且 ,连接 和 .
(1)求证: ;
(2)如图2,将菱形 绕着点A旋转,当菱形 旋转到使点C落在线段 上时( ),求点F到 的距离. 21教育名师原创作品
18.如图,在△A_BC??????AB_=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE,CF相交于点D. 21*cnjy*com
?
(1)求证:BE=CF;
(2)当α=90°时,求四边形AEDC的面积.
答案解析部分
一、单选题
1.【答案】 D
解:矩形的对角线相等,菱形的对角线互相垂直.
矩形具有而菱形不具有的性质是对角线相等.
故答案为:D.
2.【答案】 C
解:_è§????A????????_AC⊥BD时,四边形ABCD是菱形,故A错误;
B、当AC=BD时,四边形ABCD是矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、 当AB=BC时,四边形ABCD是菱形,故D错误.
故答案为:C.
3.【答案】 A
解:能判定四边形ABCD是菱形的是AC⊥BD,理由如下:
∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:A.
4.【答案】 D
解:证明:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DHG是由△DBC旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在RT△ADE和RT△GDE中,
?
∴Rt△AED≌Rt△GED(HL),故②正确;
∴∠ADE=∠EDG=22.5°,AE=EG,
∴∠AED=∠AFE=67.5°,
∴AE=AF=EG,
又∵∠H=∠DBC=∠DAC=45°,
∴GH∥AC,
∴四边形AEGF是菱形,故①正确;
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=90°+22.5°=112.5°,故③正确;21cnjy.com
∵正方形ABCD的边长为1,
∴∠BCD=∠BAD=90°,∠CBD=45°,BD= ,AD=CD=1.
由旋转的性质可知:∠HGD=BCD=90°,∠H=∠CBD=45°,BD=HD,GD=CD,
∴HA=BG= -1,∠H=∠EBG=45°,∠HAE=∠BGE=90°,
∴△HAE和△BGE均为直角边为 -1的等腰直角三角形,
∴FG=AE= -1 ,故④正确.
综上所述:正确的结论有①②③④.
故答案为:D.
5.【答案】 C
解:∵在菱形ABCD中,∠ABC=80°,
∴∠ABD= ABC=40°,AD∥BC,
∴∠BAD=180°﹣∠ABC=100°,
∵△ABE是等腰三角形,
∴AE=BE,或AB=BE,
当AE=BE时,
∴∠ABE=∠BAE=40°,
∴∠DAE=100°﹣40°=60°;
当AB=BE时,∴∠BAE=∠AEB= (180°﹣40°)=70°,
∴∠DAE=100°﹣70°=30°,
综上所述,当△ABE是等腰三角形时,∠DAE=30°或60°,
故答案为:C.
6.【答案】 A
解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥BD,AO= AC=4,BO= BD=3,
在Rt△AOB中,由勾股定理得:
AB= ,
∵DE⊥AB,
∴S菱形= ·BD·AC=AB·DE,
即 ×6×8=5·DE,
解得:DE= =4.8,
故答案为:A.
7.【答案】 C
解:如图,由题意得:菱形ABCD的周长为8, ,
,
是等边三角形,
,
,
该菱形较短的对角线长为 ,
故答案为:C.
8.【答案】 B
解:如图,
∵四边形ABCD是菱形,
∴OA=OC=AC,OB=OD=BD,AC⊥BD,
∵ 两条对角线长的比是4:3 ,
∴OA:OD=4:3 ,
设OA=4x,OD=3x,
∵OA2+OB2=AB2 ,
∴16x2+9x2=25,
解得x=1,
∴OA=4,OD=3,
∴AC=8,BD=6,
∴S=AC·BD=×8×6=24(cm2).
故答案为:B.
9.【答案】 D
解:连接DE交AC于P,连接BD,BP,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,
∴PE+PB=PE+PD=DE,
即DE就是PE+PB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∴AD=BD,
∵AE=BE=AB=1,
∴DE⊥AB,
在Rt△ADE中,DE=,
∴ PE+PB的最小值是.
故答案为:D.
10.【答案】 D
解:过点D作DE⊥AB,垂足为E;过点D作DF⊥BC,垂足为F. (如图)
根据辅助线作法和纸条宽度的定义可知:∠AED=∠CFD=90°,DE=DF=1,
由纸条的几何特征可知,AD∥BC,AB∥DC,故四边形ABCD为平行四边形,
由题目条件和对顶角关系可知,∠BCD=60°,
∴在平行四边形ABCD中,∠BAD=∠BCD=60°,即∠EAD=∠FCD=60°,
∵在△AED与△CFD中:
,
∴△AED≌△CFD (AAS)
∴AD=CD,
∴平行四边形ABCD为菱形,
∵在Rt△CFD中,∠FCD=60°,
∴∠FDC=30°,
∴在Rt△CFD中, ,
∴在Rt△CFD中, ,
∴ ,
∵在菱形ABCD中,BC=CD,
∴ ,
∴菱形ABCD的面积为: ,即纸片重叠部分的面积为 .
故答案为:D.
二、填空题
11.【答案】 30
解:菱形的面积等于两对角线的积的一半,则这个菱形的面积是6×10× =30cm2.
故答案为:30.
12.【答案】
解:∵菱形ABCD中,∠BAD=120°,
∴∠BAC= ∠BAD=60°,AC⊥BD,
∴∠ABO=30°,
∵BD=6 ,
∴BO=3 ,
设AO=x,则AB=2x,
故x2+(3 )2=(2x)2 ,
解得:x=3,
∴AO=3,
∴AC=6,
∴菱形的面积=6 ×6÷2=18 .
故答案为:18 .
13.【答案】
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC= ×4=2,∠BAC= ∠BAD= ×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB= ,
∴BD=2OB= ,
∴该菱形的面积是: AC?BD= ×4× = ,
故答案为: .
14.【答案】 2.4
解:∵菱形ABCD中,AC=6,BD=8,
∴OA=OC= AC=3,OB= BD=4,AC⊥BD,
∴BC= = =5,
∵S△OBC= ×OC×OB= ×BC×OE,
∴OE= =2.4,
故答案为:2.4.
三、综合题
15.【答案】 证明:∵△ABC为等腰三角形,AH⊥BC,∴H为BC的中点,
又∵FH=EH,∴四边形BECF为平行四边形.
∵AH⊥BC,∴平行四边形BECF为菱形.
16.【答案】 (1)解: 四边形 是菱形,
是等边三角形,
菱形 的周长
(2)证明:
四边形 是平行四边形,
四边形 是菱形
四边形 是矩形
17.【答案】 (1)证明:∵四边形ABCD和四边形AEFG为菱形
∴GA=EA,OA=BA
∵∠DAB=∠GAE=60°
∴∠GAD+∠DAE=60°
∠DAE+∠EAB=60°
∴∠GAD=∠EAB
∴△GAD≌△EAB(SAS)
∴DG=BE
(2)解:延长FE,AB交于点H
∵AC是菱形ABCD对角线
∴∠CAB= ∠DAB=30°
∵∠GAE=60°且四边形AEGF是菱形
∴GA∥FE
∴∠FEA=180°-60°=120°
∴∠AEH=180°-120°=60°
∵∠EAB=30°
∴∠H=90°
∵AE=4,在Rt△EAH=30°
∴EH=2
∴F到AB的距离为4+2=6
18.【答案】 (1)证明:∵将△ABC绕点A按顺时针方向旋转角α得到△AEF,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴AB=AC=AE=AF,∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC.
在△AEB和△AFC中,
∴△AEB≌△AFC(SAS),
∴BE=CF.
(2)解:∵α=90°,
∴∠EAB=∠FAC=90°.
∵AE=AB,
∴△ABE为等腰直角三角形,
∴∠ABE=45°,
∴∠ABE=∠BAC,
∴AC∥BE,
同理可得AE∥CF.
∵AE=AC,
∴四边形AEDC为菱形.
设AF与BE交于点H.
∵∠EAF=45°,
∴AH平分∠EAB,
∴AH⊥BE,
∴△AHE为等腰直角三角形,
∴AH=AE·sin45° AE= ,
∴四边形AEDC的面积为AH·DE= ×2=2 .
_21?????????è?????(www.21cnjy.com)_
