第18章 平行四边形 单元测试卷(含解析)
文档属性
| 名称 | 第18章 平行四边形 单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 15:30:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第18章测试卷
一、单选题
1.如图,四边_???ABCD???_,AB∥CD,BC∥AD,点E、F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为(?? ) 21·cn·jy·com
A.?∠1=∠2????????????????????????????B.?BF=DE????????????????????????????C.?AE=CF????????????????????????????D.?∠AED=∠CFB
2.如图,将 绕边 的中点O顺时针旋转180°.嘉淇发现,旋转后的 与 构成平行四边形,并推理如下: www.21-cn-jy.com
点A,C分别转到了点C,A处,
而点B转到了点D处.
∵ ,
∴四边形 是平行四边形.
小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是(??? )21cnjy.com
A.?嘉淇推理严谨,不必补充????????????????????????????????????B.?应补充:且 ,
C.?应补充:且 ??????????????????????????????????????????D.?应补充:且 ,2·1·c·n·j·y
3.小军不慎将一块_???è?????è????????_璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(?? ) 21·世纪*教育网
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
4.在平行四边形 中, ,则 的度数(??? )
A.?120°?????????????????????????????????????B.?60°?????????????????????????????????????C.?30°?????????????????????????????????????D.?150°
5.如图,在?ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是(?? )
A.???????????????????????????????????????????B.?2??????????????????????????????????????????C.???????????????????????????????????????????D.?3
6.如图,在 中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是(?? )
A.?5 ???????????????????????????????????B.?6 ???????????????????????????????????C.?4 ???????????????????????????????????D.?5
二、填空题
7.如图,B(2,﹣2),C(3,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为________. www-2-1-cnjy-com
8.如图,平行四边形 中, , 相交于点 ,若 , ,则△ 的周长为________. 【出处:21教育名师】
9.如图,在四边形 中,连接 , .请你添加一个条件________,使 .(填一种情况即可) 21*cnjy*com
10.如图,平行四边形ABCD的对角线AC,BD交于点O,E,F是对角线AC上两点,给出下列4个条件:① ;②DE=BF;③ ;④ ,其中不能判定四边形DEBF是平行四边形的是________;
三、综合题
11.如图,四边形 ABCD 和四边形 CDEF 均为平行四边形,连接 AE,BF.求证:AE=BF.
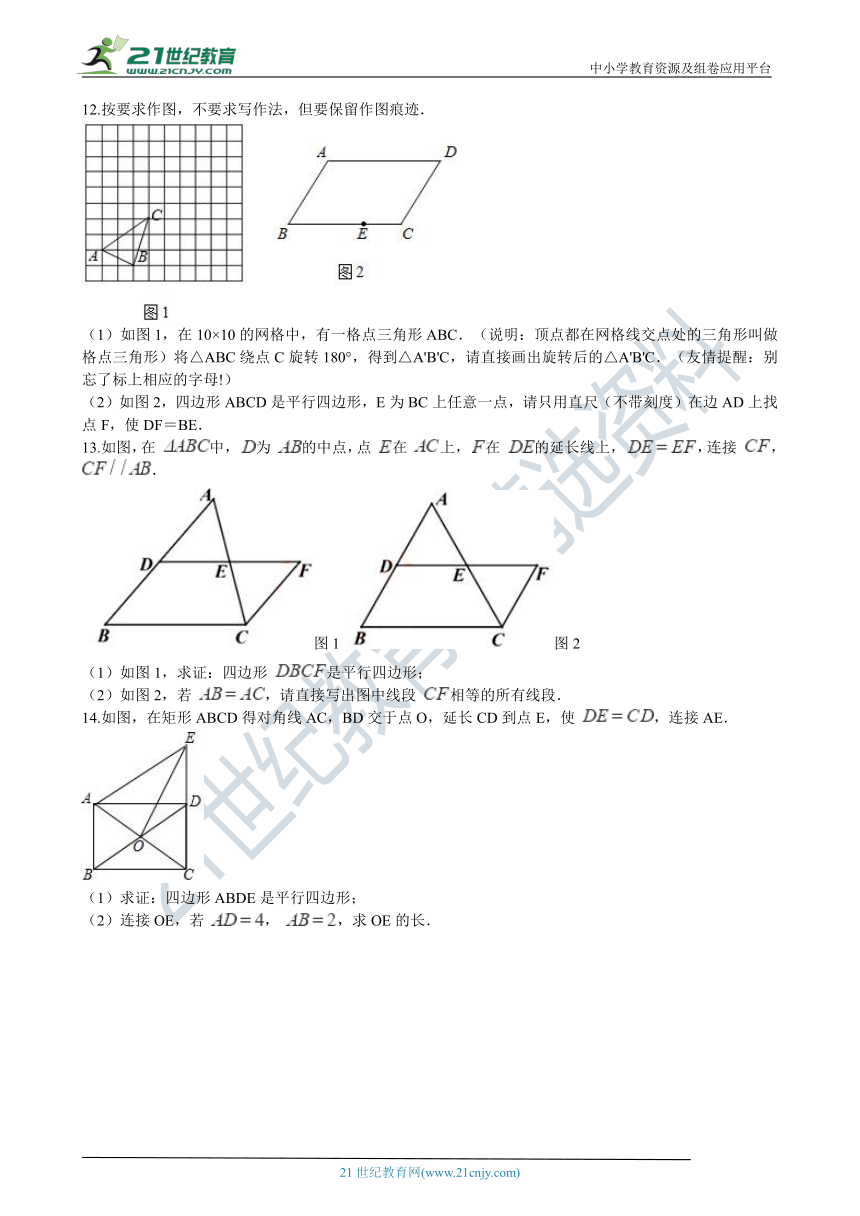
12.按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,在10×10的网格_??????????????????_三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)将△ABC绕点C旋转180°,得到△A'B'C,请直接画出旋转后的△A'B'C.(友情提醒:别忘了标上相应的字母!) 21教育名师原创作品
(2)如图2,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.
13.如图,在 中, 为 的中点,点 在 上, 在 的延长线上, ,连接 , .
图1 图2
(1)如图1,求证:四边形 是平行四边形;
(2)如图2,若 ,请直接写出图中线段 相等的所有线段.
14.如图,在矩形ABCD得对角线AC,BD交于点O,延长CD到点E,使 ,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)连接OE,若 , ,求OE的长.
答案解析部分
一、单选题
1.【答案】 C
解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,∠ABE=∠CDF,
∴AB=CD,
当添加∠1=∠2时,由ASA判定△ABE≌△CDF,
∴选项A正确;
当添加BF=DE时,BE=DF,由SAS判定△ABE≌△CDF,
∴选项B正确;
当添加AE=CF时,由SSA不能判定△ABE≌△CDF,
∴选项C不正确;
当∠AED=∠CFB时,由AAS判定△ABE≌△CDF,
∴选项D正确;
故答案为:C.
2.【答案】 B
解:根据旋转的性质得: CB=AD,AB=CD,
∴四边形ABDC是平行四边形;
故应补充“AB=CD”,
故答案为:B.
3.【答案】 C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点, 【版权所有:21教育】
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为:C.
4.【答案】 B
解:∵平行四边形ABCD
∴AD∥BC,∠A=∠C
∴∠A+∠B=180°
∵∠A:∠B=2:1
∴∠A=120°
∴∠B=60°
故答案为:B.
5.【答案】 B
解:∵四边形ABCD为平行四边形,
∴AB∥CD,CD=AB=6,
∴∠ABE=∠CEB,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠CEB,
∴CE=BC=4,
∴DE=CD﹣CE=6﹣4=2.
故答案为:B.
6.【答案】 C
解:∵CE平分∠BCD,
∴∠BCE=∠DCE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠BCE,
∴BC=BE=5,
∴AD=5,
∵EA=3,ED=4,
在△AED中, ,即 ,
∴∠AED=90°,
∴CD=AB=3+5=8,∠EDC=90°,
在Rt△EDC中, .
故答案为:C.
二、填空题
7.【答案】 y=
解:设A坐标为(x,y),
∵B(2,﹣2),C(3,0),以OC,CB为边作平行四边形OABC,
∴x+3=0+2,y+0=0﹣2,
解得:x=﹣1,y=﹣2,即A(﹣1,﹣2),
设过点A的反比例解析式为y= ,
把A(﹣1,﹣2)代入得:k=2,
则过点A的反比例函数解析式为y= ,
故答案为:y= .
8.【答案】 14
解:_??????è?????è?????_ABCD,
∴AC=2OC,BD=2OB,AD=BC=6
∵AC+BD=16
∴2OC+2OB=16
∴OC+OB=8
∴△BCO的周长为OC+OB+BC=8+6=14.
故答案为:14.
9.【答案】 AD=BC(答案不唯一)
解:添加的条件:AD=BC,理由是:
∵∠ACB=∠CAD,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD.
10.【答案】 ②③
解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
又∵OE=OF,
∴四边形DEBF是平行四边形,故①正确,不符合题意;
当DE=BF时,根据已知条件不能证明四边形DEBF是平行四边形,故②符合题意;
当 时,不能证明四边形DEBF是平行四边形,故③符合题意;
当 时,根据已知可得 , ,
∴ ,
∴ , ,
∴ ,
∴ ,
∴四边形DEBF是平行四边形;故④正确,不符合题意.
故答案为:②③.
三、综合题
11.【答案】 证明:∵四边形 ABCD,CDEF 均为平行四边形,
∴AB ∥ CD,AB=CD,CD ∥ EF,CD=EF,
∴AB ∥ EF,AB=EF,
∴四边形 ABFE 为平行四边形,
∴AE=BF.
12.【答案】 (1)解:如图1,△A′B′C即为所求;
(2)解:如图2:
连接AC、BD交于点O,作直线EO交AD于F,点F即为所求.
理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,BO=DO,
∴∠FDO=∠EBO,
又∵∠FOD=∠EOB,
∴△BOE≌△DOF(ASA),
∴BE=DF.
13.【答案】 (1)证明:∵CF∥AB,
∴∠A=∠ECF.
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS).
∴AD=CF.
∵D是AB的中点,
∴AD=BD.
∴BD=CF,且BD∥CF.
∴四边形DBCF是平行四边形.
(2)解:与CF相等的线段有AD、BD 、AE、CE.
理由是:∵四边形DBCF是平行四边形,
∴BD=CF.
由(1)△ADE≌△CFE得: AE=CE= AC.
∵D是AB的中点,
∴AD=BD= AB.
∵AB=AC,
∴CF=AE=CE=AD=BD.
14.【答案】 (1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∵DE=CD,
∴DE=AB,
∴四边形ABDE是平行四边形.
(2)解:如图所示,过O作OF⊥CD于F,
∵四边形ABCD是矩形,
∴OD=OC,
∴F是CD的中点,
∴DF= CD= ×2=1,
又∵DE=CD=AB=2,
∴EF=3,
∵O是AC的中点,
∴OF是△ACD的中位线,
∴OF= AD=2,
∴Rt△OEF中,OE= .
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第18章测试卷
一、单选题
1.如图,四边_???ABCD???_,AB∥CD,BC∥AD,点E、F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为(?? ) 21·cn·jy·com
A.?∠1=∠2????????????????????????????B.?BF=DE????????????????????????????C.?AE=CF????????????????????????????D.?∠AED=∠CFB
2.如图,将 绕边 的中点O顺时针旋转180°.嘉淇发现,旋转后的 与 构成平行四边形,并推理如下: www.21-cn-jy.com
点A,C分别转到了点C,A处,
而点B转到了点D处.
∵ ,
∴四边形 是平行四边形.
小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是(??? )21cnjy.com
A.?嘉淇推理严谨,不必补充????????????????????????????????????B.?应补充:且 ,
C.?应补充:且 ??????????????????????????????????????????D.?应补充:且 ,2·1·c·n·j·y
3.小军不慎将一块_???è?????è????????_璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(?? ) 21·世纪*教育网
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
4.在平行四边形 中, ,则 的度数(??? )
A.?120°?????????????????????????????????????B.?60°?????????????????????????????????????C.?30°?????????????????????????????????????D.?150°
5.如图,在?ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是(?? )
A.???????????????????????????????????????????B.?2??????????????????????????????????????????C.???????????????????????????????????????????D.?3
6.如图,在 中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是(?? )
A.?5 ???????????????????????????????????B.?6 ???????????????????????????????????C.?4 ???????????????????????????????????D.?5
二、填空题
7.如图,B(2,﹣2),C(3,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为________. www-2-1-cnjy-com
8.如图,平行四边形 中, , 相交于点 ,若 , ,则△ 的周长为________. 【出处:21教育名师】
9.如图,在四边形 中,连接 , .请你添加一个条件________,使 .(填一种情况即可) 21*cnjy*com
10.如图,平行四边形ABCD的对角线AC,BD交于点O,E,F是对角线AC上两点,给出下列4个条件:① ;②DE=BF;③ ;④ ,其中不能判定四边形DEBF是平行四边形的是________;
三、综合题
11.如图,四边形 ABCD 和四边形 CDEF 均为平行四边形,连接 AE,BF.求证:AE=BF.
12.按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,在10×10的网格_??????????????????_三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)将△ABC绕点C旋转180°,得到△A'B'C,请直接画出旋转后的△A'B'C.(友情提醒:别忘了标上相应的字母!) 21教育名师原创作品
(2)如图2,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.
13.如图,在 中, 为 的中点,点 在 上, 在 的延长线上, ,连接 , .
图1 图2
(1)如图1,求证:四边形 是平行四边形;
(2)如图2,若 ,请直接写出图中线段 相等的所有线段.
14.如图,在矩形ABCD得对角线AC,BD交于点O,延长CD到点E,使 ,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)连接OE,若 , ,求OE的长.
答案解析部分
一、单选题
1.【答案】 C
解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,∠ABE=∠CDF,
∴AB=CD,
当添加∠1=∠2时,由ASA判定△ABE≌△CDF,
∴选项A正确;
当添加BF=DE时,BE=DF,由SAS判定△ABE≌△CDF,
∴选项B正确;
当添加AE=CF时,由SSA不能判定△ABE≌△CDF,
∴选项C不正确;
当∠AED=∠CFB时,由AAS判定△ABE≌△CDF,
∴选项D正确;
故答案为:C.
2.【答案】 B
解:根据旋转的性质得: CB=AD,AB=CD,
∴四边形ABDC是平行四边形;
故应补充“AB=CD”,
故答案为:B.
3.【答案】 C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点, 【版权所有:21教育】
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为:C.
4.【答案】 B
解:∵平行四边形ABCD
∴AD∥BC,∠A=∠C
∴∠A+∠B=180°
∵∠A:∠B=2:1
∴∠A=120°
∴∠B=60°
故答案为:B.
5.【答案】 B
解:∵四边形ABCD为平行四边形,
∴AB∥CD,CD=AB=6,
∴∠ABE=∠CEB,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠CEB,
∴CE=BC=4,
∴DE=CD﹣CE=6﹣4=2.
故答案为:B.
6.【答案】 C
解:∵CE平分∠BCD,
∴∠BCE=∠DCE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠BCE,
∴BC=BE=5,
∴AD=5,
∵EA=3,ED=4,
在△AED中, ,即 ,
∴∠AED=90°,
∴CD=AB=3+5=8,∠EDC=90°,
在Rt△EDC中, .
故答案为:C.
二、填空题
7.【答案】 y=
解:设A坐标为(x,y),
∵B(2,﹣2),C(3,0),以OC,CB为边作平行四边形OABC,
∴x+3=0+2,y+0=0﹣2,
解得:x=﹣1,y=﹣2,即A(﹣1,﹣2),
设过点A的反比例解析式为y= ,
把A(﹣1,﹣2)代入得:k=2,
则过点A的反比例函数解析式为y= ,
故答案为:y= .
8.【答案】 14
解:_??????è?????è?????_ABCD,
∴AC=2OC,BD=2OB,AD=BC=6
∵AC+BD=16
∴2OC+2OB=16
∴OC+OB=8
∴△BCO的周长为OC+OB+BC=8+6=14.
故答案为:14.
9.【答案】 AD=BC(答案不唯一)
解:添加的条件:AD=BC,理由是:
∵∠ACB=∠CAD,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD.
10.【答案】 ②③
解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
又∵OE=OF,
∴四边形DEBF是平行四边形,故①正确,不符合题意;
当DE=BF时,根据已知条件不能证明四边形DEBF是平行四边形,故②符合题意;
当 时,不能证明四边形DEBF是平行四边形,故③符合题意;
当 时,根据已知可得 , ,
∴ ,
∴ , ,
∴ ,
∴ ,
∴四边形DEBF是平行四边形;故④正确,不符合题意.
故答案为:②③.
三、综合题
11.【答案】 证明:∵四边形 ABCD,CDEF 均为平行四边形,
∴AB ∥ CD,AB=CD,CD ∥ EF,CD=EF,
∴AB ∥ EF,AB=EF,
∴四边形 ABFE 为平行四边形,
∴AE=BF.
12.【答案】 (1)解:如图1,△A′B′C即为所求;
(2)解:如图2:
连接AC、BD交于点O,作直线EO交AD于F,点F即为所求.
理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,BO=DO,
∴∠FDO=∠EBO,
又∵∠FOD=∠EOB,
∴△BOE≌△DOF(ASA),
∴BE=DF.
13.【答案】 (1)证明:∵CF∥AB,
∴∠A=∠ECF.
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS).
∴AD=CF.
∵D是AB的中点,
∴AD=BD.
∴BD=CF,且BD∥CF.
∴四边形DBCF是平行四边形.
(2)解:与CF相等的线段有AD、BD 、AE、CE.
理由是:∵四边形DBCF是平行四边形,
∴BD=CF.
由(1)△ADE≌△CFE得: AE=CE= AC.
∵D是AB的中点,
∴AD=BD= AB.
∵AB=AC,
∴CF=AE=CE=AD=BD.
14.【答案】 (1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∵DE=CD,
∴DE=AB,
∴四边形ABDE是平行四边形.
(2)解:如图所示,过O作OF⊥CD于F,
∵四边形ABCD是矩形,
∴OD=OC,
∴F是CD的中点,
∴DF= CD= ×2=1,
又∵DE=CD=AB=2,
∴EF=3,
∵O是AC的中点,
∴OF是△ACD的中位线,
∴OF= AD=2,
∴Rt△OEF中,OE= .
_21?????????è?????(www.21cnjy.com)_
