第19章 矩形、菱形与正方形 单元测试卷(含解析)
文档属性
| 名称 | 第19章 矩形、菱形与正方形 单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 15:34:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学华师大版八年级下学期 第19章测试卷
一、单选题
1.如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为(? )
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?3??????????????????????????????????????????D.?5
2.矩形、菱形、正方形的对角线都具有的性质是( ??)
A.?对角线互相平分?????????????B.?对角线相等?????????????C.?对角线互相垂直?????????????D.?对角线互相垂直平分
3.如图,在菱形ABCD中,两条对角线AC=12,BD=16,则此菱形的边长为( )
A.?10???????????????????????????????????????????B.?8???????????????????????????????????????????C.?6???????????????????????????????????????????D.?5
4.如图,在 中, , , ,则 的面积为(??? )
A.?6?????????????????????????????????????????B.?12?????????????????????????????????????????C.?24?????????????????????????????????????????D.?48
5.若一个圆内接正多边形的内角是 ,则这个多边形是(?? )
A.?正五边形???????????????????????????B.?正六边形???????????????????????????C.?正八边形???????????????????????????D.?正十边形
二、填空题
6.如图,E、F分别是正_??????ABCD_的边CD、AD上的点,且CE=DF , AE、BF相交于点O , 下列结论:①AE=BF;②AE⊥BF;③S△AOB=S四边形DEOF;④AO=OE;⑤∠AFB+∠AEC=180°,其中正确的有________(填写序号). 21世纪教育网版权所有
7.如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm , DE: :2,则FC的长度为________ cm. 21·cn·jy·com
8.如图,菱形ABCD对角线AC,BD交于点O,∠BAD=60°,点E是AD的中点,OE=4,则菱形ABCD的面积为________? www.21-cn-jy.com
9.如图,菱_???ABCD???_对角线AC、BD相交于点O , OH⊥AB于H . 若菱形ABCD的周长为16,∠BAD=60°,则OH=________. 2-1-c-n-j-y
10.如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,请你计算: 21*cnjy*com
(1)如果标注A、B的正方形边长分别为5,6,则标注G的正方形的边长 ________;
(2)如果标注A、B的正方形边长分别为x,y,则标注E的正方形的边长 ________.(用含x,y的代数式表示) 【出处:21教育名师】
三、综合题
11.如图,已知E是矩形ABCD一边AD的中点,延长AB至点F连接CE,EF,CF,得到 .且 , , .求CE的长; 21教育名师原创作品
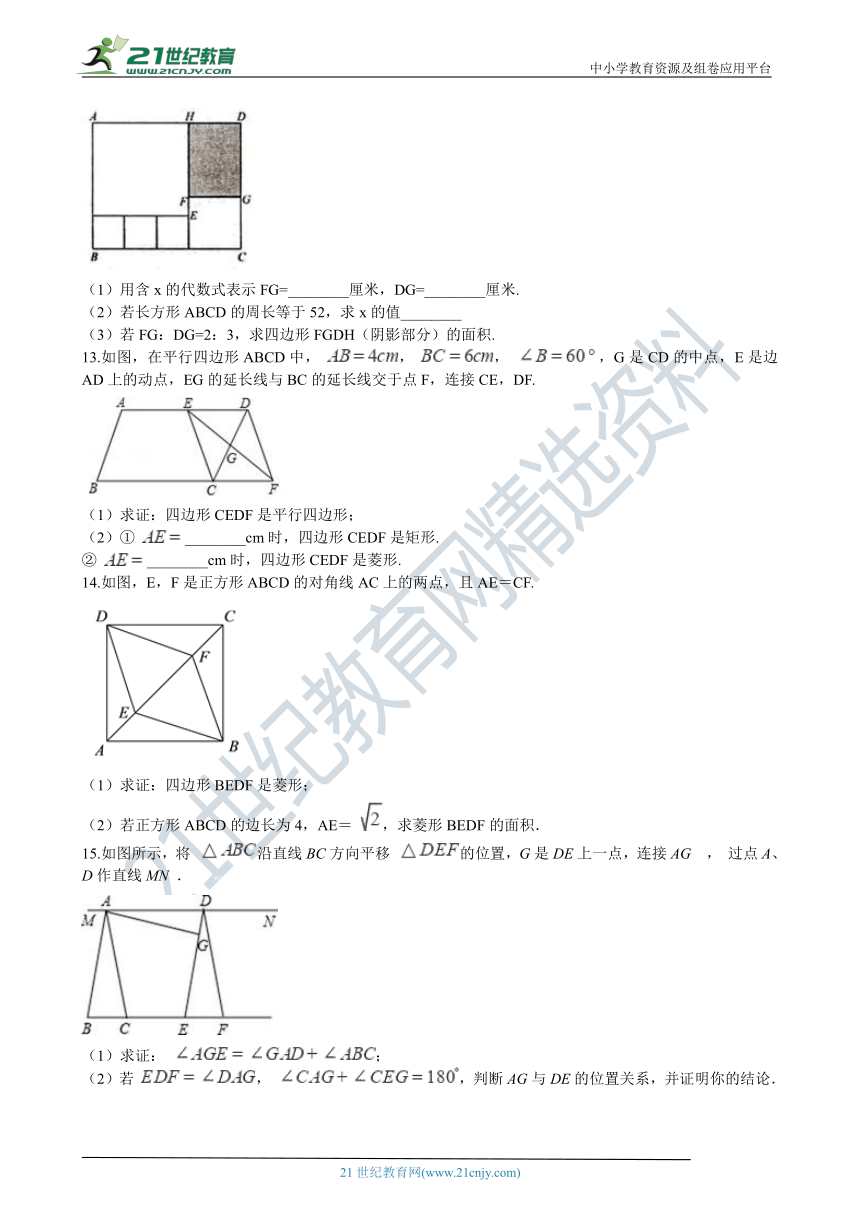
12.如图所示,用三种大小不同的5个正方形和一个长方形(阴影部分)拼成长方形ABCD,其中EF=2厘米,最小的正方形的边长为x厘米.
(1)用含x的代数式表示FG=________厘米,DG=________厘米.???
(2)若长方形ABCD的周长等于52,求x的值________
(3)若FG:DG=2:3,求四边形FGDH(阴影部分)的面积.
13.如图,在平行四边形ABCD中, , , ,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)① ________cm时,四边形CEDF是矩形.
② ________cm时,四边形CEDF是菱形.
14.如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE= ,求菱形BEDF的面积.
15.如图所示,将 沿直线BC方向平移 的位置,G是DE上一点,连接AG , 过点A、D作直线MN . www-2-1-cnjy-com
(1)求证: ;
(2)若 , ,判断AG与DE的位置关系,并证明你的结论.
答案解析部分
一、单选题
1.【答案】 A
解:∵ABCD是矩形,
∴OA=OB=OC,
∵∠AOB=60°,
∴∠ACB=30°,
∵AC=8,
∴AB= ,
故答案为:A.
2.【答案】 A
解:根据矩形、菱形、正方形的对角线相互平分的性质,可知选A.
故答案为:A.
3.【答案】 A
解:∵四边形ABCD是菱形,
∴OA= AC= ×12=6,OB= BD= ×16=8,AC⊥BD,
∴AB= =10.
∴此菱形的边长为10.
故答案为:A.
4.【答案】 C
解:∵四边形 是平行四边形,
∴ , ,
∴ ,
∴ ,即 ,
∴ 是菱形,
∴ 的面积 ;
故答案为:C.
5.【答案】 A
解:_???????¤?_角=180°-108°=72°,
∴n=360°÷72°=5;
故答案为:A.
二、填空题
6.【答案】 ①②③⑤
解:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=AD=CD ,
∵CE=DF ,
∴AD﹣DF=CD﹣CE , 即AF=DE ,
∴△ABF≌△DAE(SAS),
∴∠ABF=∠DAE , AE=BF , 故①符合题意;
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
∴∠AOB=90°,
∴AE⊥BF , 故②符合题意;
∵△ABF≌△DAE ,
∴S△ABF=S△DAE ,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF ,
即S△AOB=S四边形DEOF , 故③符合题意;
假设AO=OE , 连接BE , 如图,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC ,
∴AB>BC , 这与正方形的边长AB=BC相矛盾,
所以假设不成立,∴AO≠OE , 故④不符合题意;
∵△ABF≌△DAE ,
∴∠AFB=∠AED ,
∴∠AFB+∠AEC=∠AED+∠AEC=180°,故⑤符合题意;
综上所述,正确的有①②③⑤.
故答案为:①②③⑤.
7.【答案】 3
解: 四边形ABCD是矩形,
, , ,
根据折叠的性质得: , ,
: :2,
, ,
,
,
设 ,则 ,
根据勾股定理得: ,
即 ,
解得: ,
.
故答案为3.
8.【答案】 32
解:∵四边形ABCD是菱形,
∴AB=AD,OB=OD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∵AE=DE,OB=OD,
∴AB=2OE=8,
∴S菱形ABCD=2?S△ABD= .
故答案是: .
9.【答案】
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD, BO=DO,
∵菱形ABCD的周长为16,
∴AB=AD=4,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=4,∠ABD=60°,
∴BO=DO=2,
在Rt△OBH中,∠ABD=60°,BO =2,
∴ ,
∴OH=2 .
故答案为: .
10.【答案】 (1)23
(2)3y-3x
解:(1)∵A、B的正方形边长分别为5,6,
∴正方形C的边长为5+6=11,
∴正方形D的边长为11+6=17,
∴正方形G的边长为17+6=23,
故答案为:23;
( 2 )∵A、B的正方形边长分别为x、y,
∴正方形C的边长为x+y,
∴正方形D的边长为x+y+y=x+2y,
∴正方形G的边长为x+2y+y=x+3y,
∴正方形H的边长为x+3y+(y-x)=4y,
∴正方形M的边长为4y-x,
∴正方形E的边长为4y-x-x-(x+y)=3y-3x,
故答案为:3y-3x.
三、综合题
11.【答案】 解: 四边形 是矩形, ,
, ,
,
,
中, , , ,
根据勾股定理得 ,
,
∴矩形 中, ,
是 的中点,
,
中, , , ,
根据勾股定理得, .
12.【答案】 (1)(x+2);(3x-2)
(2)3
(3)解:由题(1)知,
代入 得:
解得:
则
故四边形FGDH的面积为 .
解:(1)由图可知, ,GC等于最小正方形的边长与EF之和
则
由图可知,最大正方形的边长是最小正方形边长的3倍,即为
则 ;
( 2 )由图可知, ,
则长方形ABCD的周长为:
由题意得: ,解得: ; ?
13.【答案】 (1)证明: 四边形ABCD是平行四边形,
,
, ,
是CD的中点,
,
≌ ,
,而 ,
四边形CEDF是平行四边形
(2)4;2
解:(2)①当 时,四边形CEDF是矩形.
理由:作 于P,
, ,
,
四边形ABCD是平行四边形,
, , ,
,
,
≌ ,
,
平行四边形CEDF是矩形,
当 时,四边形CEDF是矩形.
故答案为4;②当 时,四边形CEDF是菱形.
理由: , .
.
, .
是等边三角形.
.
平行四边形CEDF是菱形.
当 时,四边形CEDF是菱形,
故答案为2.
14.【答案】 (1)证明:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC.
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BEDF为平行四边形,
又∵BD⊥EF,
∴四边形BEDF为菱形.
(2)解:∵正方形ABCD的边长为4,
∴BD=AC= .
∵AE=CF= ,
∴EF=AC- = ,
∴S菱形BEDF= BD·EF= × .
15.【答案】 (1)证明:由平移的性质得:△ABC≌△DEF,
∴AB=DE,AB∥DE,
∴四边形ABED为平行四边形,
∴AD∥BF,∠ADG=∠ABC,
∴∠ADG=∠DEF,
∴∠ABC=∠DEF=∠ADG,
∵∠AGE为△ADG的外角,
∴∠AGE=∠DAG+∠ADG=∠GAD+∠ABC;
(2)解:AG⊥DE,理由为:
由平移的性质得到∠EDF=∠BAC,
∵∠EDF=∠DAG,
∴∠BAC=∠DAG,
∵AB∥DE,
∴∠ABC+∠BEG=180°,
∵∠CAG+∠CEG=180°,
∴∠ABC=∠CAG,
∵MN∥BC,∴∠ABC=∠MAB,
∴∠MAB=∠CAG,
∵∠MAB+∠BAC+∠CAG+∠DAG=180°,
∴∠CAG+∠BAC=90°,即∠BAG=90°,
∵AB∥DE,
∴∠BAG+∠AGD=90°,
则AG⊥DE.
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版八年级下学期 第19章测试卷
一、单选题
1.如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为(? )
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?3??????????????????????????????????????????D.?5
2.矩形、菱形、正方形的对角线都具有的性质是( ??)
A.?对角线互相平分?????????????B.?对角线相等?????????????C.?对角线互相垂直?????????????D.?对角线互相垂直平分
3.如图,在菱形ABCD中,两条对角线AC=12,BD=16,则此菱形的边长为( )
A.?10???????????????????????????????????????????B.?8???????????????????????????????????????????C.?6???????????????????????????????????????????D.?5
4.如图,在 中, , , ,则 的面积为(??? )
A.?6?????????????????????????????????????????B.?12?????????????????????????????????????????C.?24?????????????????????????????????????????D.?48
5.若一个圆内接正多边形的内角是 ,则这个多边形是(?? )
A.?正五边形???????????????????????????B.?正六边形???????????????????????????C.?正八边形???????????????????????????D.?正十边形
二、填空题
6.如图,E、F分别是正_??????ABCD_的边CD、AD上的点,且CE=DF , AE、BF相交于点O , 下列结论:①AE=BF;②AE⊥BF;③S△AOB=S四边形DEOF;④AO=OE;⑤∠AFB+∠AEC=180°,其中正确的有________(填写序号). 21世纪教育网版权所有
7.如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm , DE: :2,则FC的长度为________ cm. 21·cn·jy·com
8.如图,菱形ABCD对角线AC,BD交于点O,∠BAD=60°,点E是AD的中点,OE=4,则菱形ABCD的面积为________? www.21-cn-jy.com
9.如图,菱_???ABCD???_对角线AC、BD相交于点O , OH⊥AB于H . 若菱形ABCD的周长为16,∠BAD=60°,则OH=________. 2-1-c-n-j-y
10.如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,请你计算: 21*cnjy*com
(1)如果标注A、B的正方形边长分别为5,6,则标注G的正方形的边长 ________;
(2)如果标注A、B的正方形边长分别为x,y,则标注E的正方形的边长 ________.(用含x,y的代数式表示) 【出处:21教育名师】
三、综合题
11.如图,已知E是矩形ABCD一边AD的中点,延长AB至点F连接CE,EF,CF,得到 .且 , , .求CE的长; 21教育名师原创作品
12.如图所示,用三种大小不同的5个正方形和一个长方形(阴影部分)拼成长方形ABCD,其中EF=2厘米,最小的正方形的边长为x厘米.
(1)用含x的代数式表示FG=________厘米,DG=________厘米.???
(2)若长方形ABCD的周长等于52,求x的值________
(3)若FG:DG=2:3,求四边形FGDH(阴影部分)的面积.
13.如图,在平行四边形ABCD中, , , ,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)① ________cm时,四边形CEDF是矩形.
② ________cm时,四边形CEDF是菱形.
14.如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE= ,求菱形BEDF的面积.
15.如图所示,将 沿直线BC方向平移 的位置,G是DE上一点,连接AG , 过点A、D作直线MN . www-2-1-cnjy-com
(1)求证: ;
(2)若 , ,判断AG与DE的位置关系,并证明你的结论.
答案解析部分
一、单选题
1.【答案】 A
解:∵ABCD是矩形,
∴OA=OB=OC,
∵∠AOB=60°,
∴∠ACB=30°,
∵AC=8,
∴AB= ,
故答案为:A.
2.【答案】 A
解:根据矩形、菱形、正方形的对角线相互平分的性质,可知选A.
故答案为:A.
3.【答案】 A
解:∵四边形ABCD是菱形,
∴OA= AC= ×12=6,OB= BD= ×16=8,AC⊥BD,
∴AB= =10.
∴此菱形的边长为10.
故答案为:A.
4.【答案】 C
解:∵四边形 是平行四边形,
∴ , ,
∴ ,
∴ ,即 ,
∴ 是菱形,
∴ 的面积 ;
故答案为:C.
5.【答案】 A
解:_???????¤?_角=180°-108°=72°,
∴n=360°÷72°=5;
故答案为:A.
二、填空题
6.【答案】 ①②③⑤
解:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=AD=CD ,
∵CE=DF ,
∴AD﹣DF=CD﹣CE , 即AF=DE ,
∴△ABF≌△DAE(SAS),
∴∠ABF=∠DAE , AE=BF , 故①符合题意;
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
∴∠AOB=90°,
∴AE⊥BF , 故②符合题意;
∵△ABF≌△DAE ,
∴S△ABF=S△DAE ,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF ,
即S△AOB=S四边形DEOF , 故③符合题意;
假设AO=OE , 连接BE , 如图,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC ,
∴AB>BC , 这与正方形的边长AB=BC相矛盾,
所以假设不成立,∴AO≠OE , 故④不符合题意;
∵△ABF≌△DAE ,
∴∠AFB=∠AED ,
∴∠AFB+∠AEC=∠AED+∠AEC=180°,故⑤符合题意;
综上所述,正确的有①②③⑤.
故答案为:①②③⑤.
7.【答案】 3
解: 四边形ABCD是矩形,
, , ,
根据折叠的性质得: , ,
: :2,
, ,
,
,
设 ,则 ,
根据勾股定理得: ,
即 ,
解得: ,
.
故答案为3.
8.【答案】 32
解:∵四边形ABCD是菱形,
∴AB=AD,OB=OD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∵AE=DE,OB=OD,
∴AB=2OE=8,
∴S菱形ABCD=2?S△ABD= .
故答案是: .
9.【答案】
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD, BO=DO,
∵菱形ABCD的周长为16,
∴AB=AD=4,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=4,∠ABD=60°,
∴BO=DO=2,
在Rt△OBH中,∠ABD=60°,BO =2,
∴ ,
∴OH=2 .
故答案为: .
10.【答案】 (1)23
(2)3y-3x
解:(1)∵A、B的正方形边长分别为5,6,
∴正方形C的边长为5+6=11,
∴正方形D的边长为11+6=17,
∴正方形G的边长为17+6=23,
故答案为:23;
( 2 )∵A、B的正方形边长分别为x、y,
∴正方形C的边长为x+y,
∴正方形D的边长为x+y+y=x+2y,
∴正方形G的边长为x+2y+y=x+3y,
∴正方形H的边长为x+3y+(y-x)=4y,
∴正方形M的边长为4y-x,
∴正方形E的边长为4y-x-x-(x+y)=3y-3x,
故答案为:3y-3x.
三、综合题
11.【答案】 解: 四边形 是矩形, ,
, ,
,
,
中, , , ,
根据勾股定理得 ,
,
∴矩形 中, ,
是 的中点,
,
中, , , ,
根据勾股定理得, .
12.【答案】 (1)(x+2);(3x-2)
(2)3
(3)解:由题(1)知,
代入 得:
解得:
则
故四边形FGDH的面积为 .
解:(1)由图可知, ,GC等于最小正方形的边长与EF之和
则
由图可知,最大正方形的边长是最小正方形边长的3倍,即为
则 ;
( 2 )由图可知, ,
则长方形ABCD的周长为:
由题意得: ,解得: ; ?
13.【答案】 (1)证明: 四边形ABCD是平行四边形,
,
, ,
是CD的中点,
,
≌ ,
,而 ,
四边形CEDF是平行四边形
(2)4;2
解:(2)①当 时,四边形CEDF是矩形.
理由:作 于P,
, ,
,
四边形ABCD是平行四边形,
, , ,
,
,
≌ ,
,
平行四边形CEDF是矩形,
当 时,四边形CEDF是矩形.
故答案为4;②当 时,四边形CEDF是菱形.
理由: , .
.
, .
是等边三角形.
.
平行四边形CEDF是菱形.
当 时,四边形CEDF是菱形,
故答案为2.
14.【答案】 (1)证明:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC.
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BEDF为平行四边形,
又∵BD⊥EF,
∴四边形BEDF为菱形.
(2)解:∵正方形ABCD的边长为4,
∴BD=AC= .
∵AE=CF= ,
∴EF=AC- = ,
∴S菱形BEDF= BD·EF= × .
15.【答案】 (1)证明:由平移的性质得:△ABC≌△DEF,
∴AB=DE,AB∥DE,
∴四边形ABED为平行四边形,
∴AD∥BF,∠ADG=∠ABC,
∴∠ADG=∠DEF,
∴∠ABC=∠DEF=∠ADG,
∵∠AGE为△ADG的外角,
∴∠AGE=∠DAG+∠ADG=∠GAD+∠ABC;
(2)解:AG⊥DE,理由为:
由平移的性质得到∠EDF=∠BAC,
∵∠EDF=∠DAG,
∴∠BAC=∠DAG,
∵AB∥DE,
∴∠ABC+∠BEG=180°,
∵∠CAG+∠CEG=180°,
∴∠ABC=∠CAG,
∵MN∥BC,∴∠ABC=∠MAB,
∴∠MAB=∠CAG,
∵∠MAB+∠BAC+∠CAG+∠DAG=180°,
∴∠CAG+∠BAC=90°,即∠BAG=90°,
∵AB∥DE,
∴∠BAG+∠AGD=90°,
则AG⊥DE.
_21?????????è?????(www.21cnjy.com)_
