2020-2021学年人教版八年级数学下册课件-18.2.2 菱形(17张)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册课件-18.2.2 菱形(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 970.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 09:08:38 | ||
图片预览





文档简介
(共17张PPT)
18.2.2菱形的判定
矩形
菱形
定义
性
质
判
定
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
具有平行四边形的一切性质
四个角都是直角
四条边都相等
对角线相等
对角线互相垂直且平分每一组对角
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
一、回顾反思
类比猜想
根据菱形的定义,可得菱形的第一个判定的方法
∵四边形ABCD是平行四边形且AB=AD
∴四边形ABCD是菱形
数学语言:
有一组邻边相等的平行四边形叫做菱形
二、探究判定条件
猜想1:
对角线互相垂直的平行四边形是菱形.
二、探究判定条件
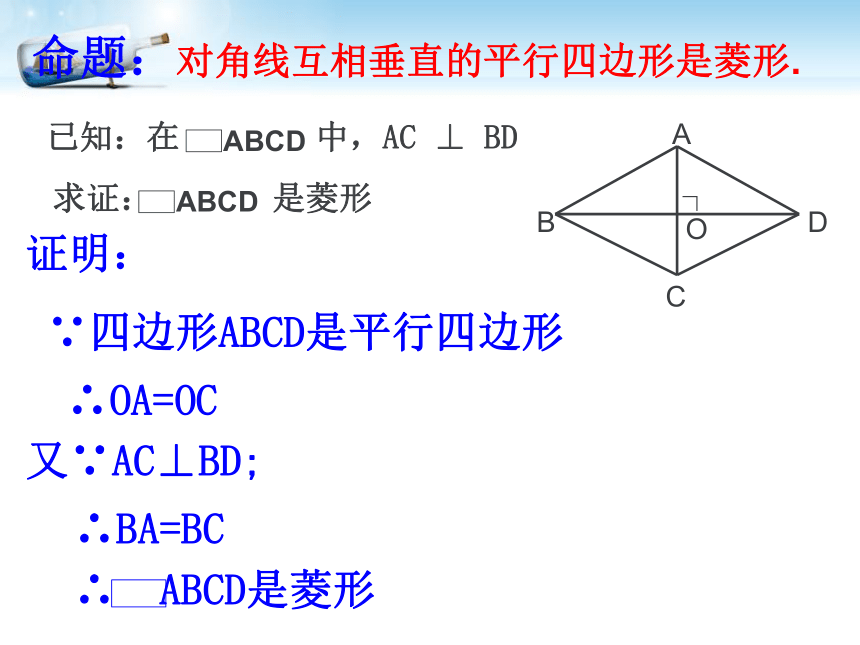
命题:对角线互相垂直的平行四边形是菱形.
已知:在
中,AC
⊥
BD
ABCD
ABCD
求证:
是菱形
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴
ABCD是菱形
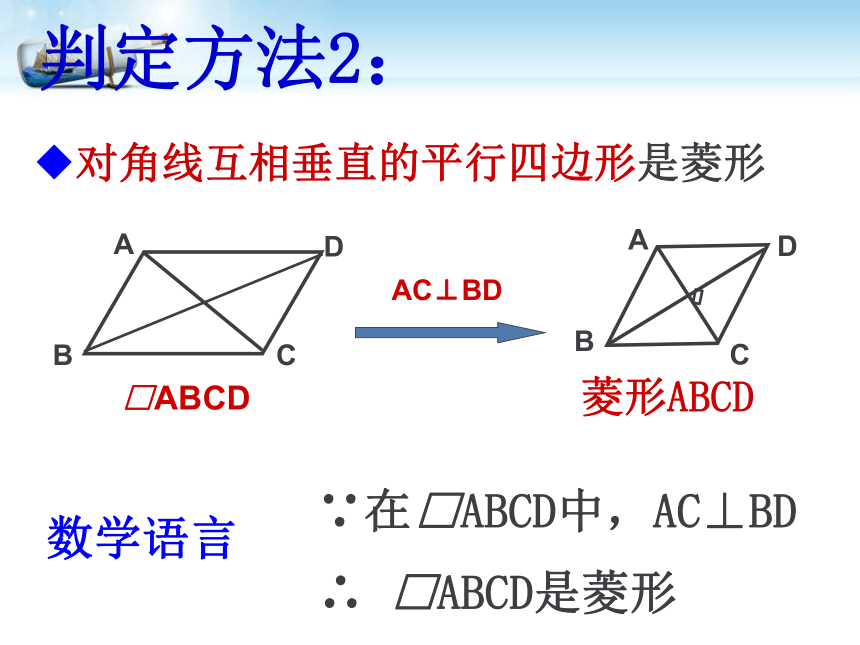
判定方法2:
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵在□ABCD中,AC⊥BD
∴
□ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
数学语言
猜想2:
有四条边相等的四边形是菱形。
二、探究判定条件
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
判定方法3:
数学语言
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
+邻边相等
=
+对角线线互相垂直=
四条边相等+
=
归纳:
1、老师说下列三个图形都是菱形,正确吗?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
3
3
4
4
┍
三、尝试练习
2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(
)
(2)对角线互相垂直平分的四边形是菱形;(
)
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(
)
╳
√
╳
∟
A
D
B
C
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
A
B
C
D
O
矩
菱
矩
菱
例1:如图,□ABCD的两条对角线AC、BD相交于点O,
AB=5,AO=4,BO=3.求证:
□ABCD是菱形.
A
B
C
D
O
∴
□ABCD是菱形.
∵
AB=5,OA
=
4
,
OB
=3
证明:
∴AC⊥BD
∴
△AOB
是直角三角形
∴
AB2
=
OA2
+
OB2
5
4
3
四、综合应用
1:已知:如图,AD平分∠BAC,DE∥AC
交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴
□AEDF是菱形
证明:
∵DE∥AC
DF∥AB
∴四边形AEDF是平行四边形
∵
DE∥AC
∴∠2=∠3
∵
AD是△ABC的角平分线
∴
∠1=∠2
∴AE=DE
∴
∠1=∠3
五、拓展延伸
A
D
C
B
∟
∟
E
F
2:把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
文字语言
图形语言
符号语言
判定法一
判定
法二
对角线互相垂直的平行四边形是菱形
判定法三
四边相等的四边形是菱形
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
六、课堂小结
18.2.2菱形的判定
矩形
菱形
定义
性
质
判
定
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
具有平行四边形的一切性质
四个角都是直角
四条边都相等
对角线相等
对角线互相垂直且平分每一组对角
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
一、回顾反思
类比猜想
根据菱形的定义,可得菱形的第一个判定的方法
∵四边形ABCD是平行四边形且AB=AD
∴四边形ABCD是菱形
数学语言:
有一组邻边相等的平行四边形叫做菱形
二、探究判定条件
猜想1:
对角线互相垂直的平行四边形是菱形.
二、探究判定条件
命题:对角线互相垂直的平行四边形是菱形.
已知:在
中,AC
⊥
BD
ABCD
ABCD
求证:
是菱形
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴
ABCD是菱形
判定方法2:
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵在□ABCD中,AC⊥BD
∴
□ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
数学语言
猜想2:
有四条边相等的四边形是菱形。
二、探究判定条件
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
判定方法3:
数学语言
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
+邻边相等
=
+对角线线互相垂直=
四条边相等+
=
归纳:
1、老师说下列三个图形都是菱形,正确吗?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
3
3
4
4
┍
三、尝试练习
2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(
)
(2)对角线互相垂直平分的四边形是菱形;(
)
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(
)
╳
√
╳
∟
A
D
B
C
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
A
B
C
D
O
矩
菱
矩
菱
例1:如图,□ABCD的两条对角线AC、BD相交于点O,
AB=5,AO=4,BO=3.求证:
□ABCD是菱形.
A
B
C
D
O
∴
□ABCD是菱形.
∵
AB=5,OA
=
4
,
OB
=3
证明:
∴AC⊥BD
∴
△AOB
是直角三角形
∴
AB2
=
OA2
+
OB2
5
4
3
四、综合应用
1:已知:如图,AD平分∠BAC,DE∥AC
交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴
□AEDF是菱形
证明:
∵DE∥AC
DF∥AB
∴四边形AEDF是平行四边形
∵
DE∥AC
∴∠2=∠3
∵
AD是△ABC的角平分线
∴
∠1=∠2
∴AE=DE
∴
∠1=∠3
五、拓展延伸
A
D
C
B
∟
∟
E
F
2:把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
文字语言
图形语言
符号语言
判定法一
判定
法二
对角线互相垂直的平行四边形是菱形
判定法三
四边相等的四边形是菱形
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
六、课堂小结
