第十八章 平行四边形 单元测试卷(Word版 含答案)
文档属性
| 名称 | 第十八章 平行四边形 单元测试卷(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 563.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 10:34:06 | ||
图片预览


文档简介
第十八章 平行四边形 单元测试卷
一、选择题
1.矩形ABCD中,AB=6,BC=8,则点A到BD的距离是( )
A.4 B.4.6 C.4.8 D.5
2.已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①④ B.①③④ C.②③ D.②③④
3.下列说法正确的是( )
①平行四边形的对角线互相平分;②菱形的四个内角相等;③矩形的对角线相等且互相垂直;④正方形具有矩形和菱形的所有性质.
A.①④ B.①③ C.②④ D.③④
4.下列命题中,正确的是( ).
A.两邻边相等的四边形是菱形 B.一条对角线平分一个内角的平行四边形是菱形
C.对角线垂直且一组邻边相等的四边形是菱形 D.对角线垂直的四边形是菱形
5.一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为( )
A.50或40或30 B.50或40 C.50 D.50或30或20
6.如图.在矩形ABCD中,对角线AC与BD交于点O,已知AO=5,∠AOB=60°,则下列选项中图形的周长是有理数的是( )
A.falseABC B.falseBOC C.falseCOD D.矩形ABCD
7.菱形false中,false.点false、false分别在边false、false上,且false.若false,则false的面积为( ).
A.false B.false C.false D.false
8.如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=40°,则∠E的度数是( )
A.10° B.20° C.30° D.40°
9.如图,正方形false和正方形false的顶点false在同一直线false上,且false,给出下列结论:
①false,
②false,
③false的面积false,
④false,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
10.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM//FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.若正方形false的对角线false的长为4,则该正方形的面积为_________.
12.已知,在△ABC中,∠BAC=45°,AB=1,AC=false,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为________.
13.已知false的周长为56,自顶点A作false于点E,false于点F,若false,false,则false_________________.
14.如图,将长,宽分别为false,1的长方形纸片剪成四个等腰三角形纸片(无余纸片).则四个等腰三角形的腰长均为_______.
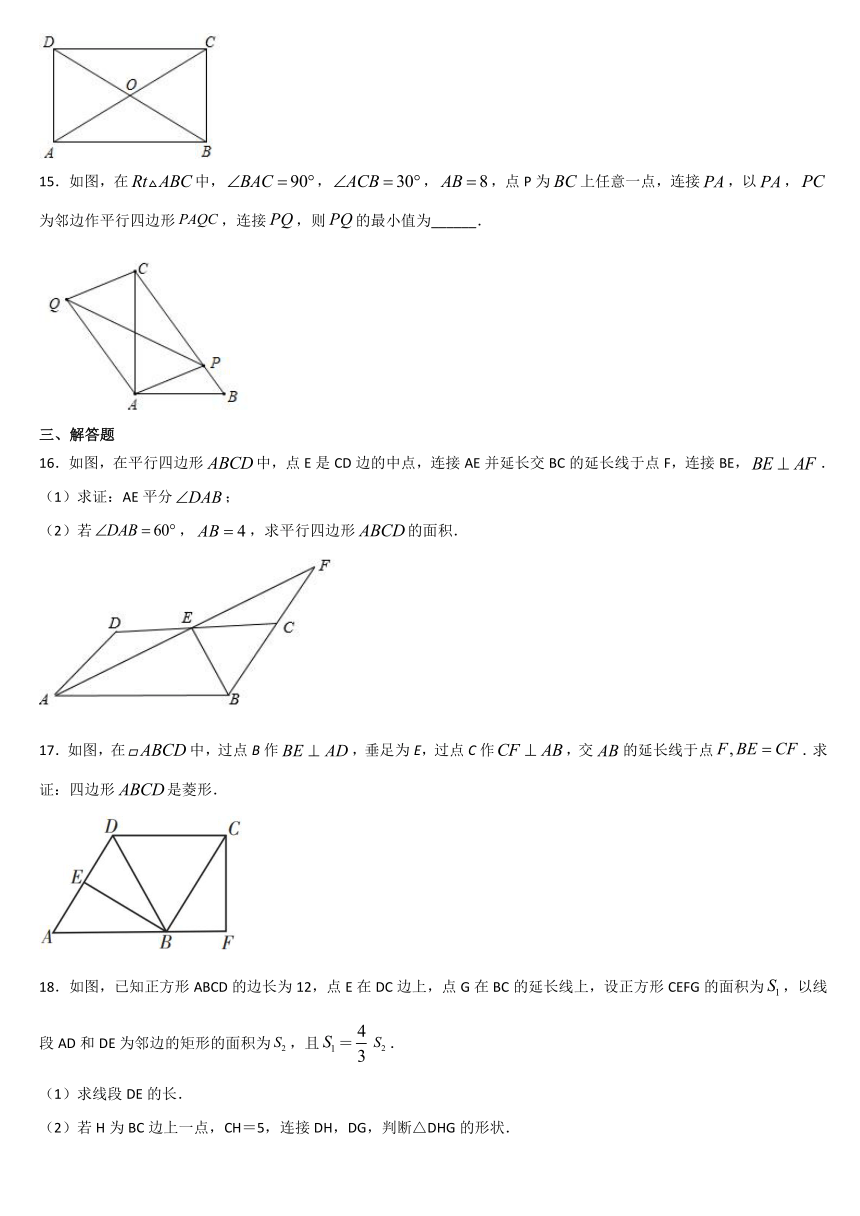
15.如图,在false中,false,false,false,点P为false上任意一点,连接false,以false,false为邻边作平行四边形false,连接false,则false的最小值为______.
三、解答题
16.如图,在平行四边形false中,点E是CD边的中点,连接AE并延长交BC的延长线于点F,连接BE,false.
(1)求证:AE平分false;
(2)若false,false,求平行四边形false的面积.
17.如图,在false中,过点B作false,垂足为E,过点C作false,交false的延长线于点false.求证:四边形false是菱形.
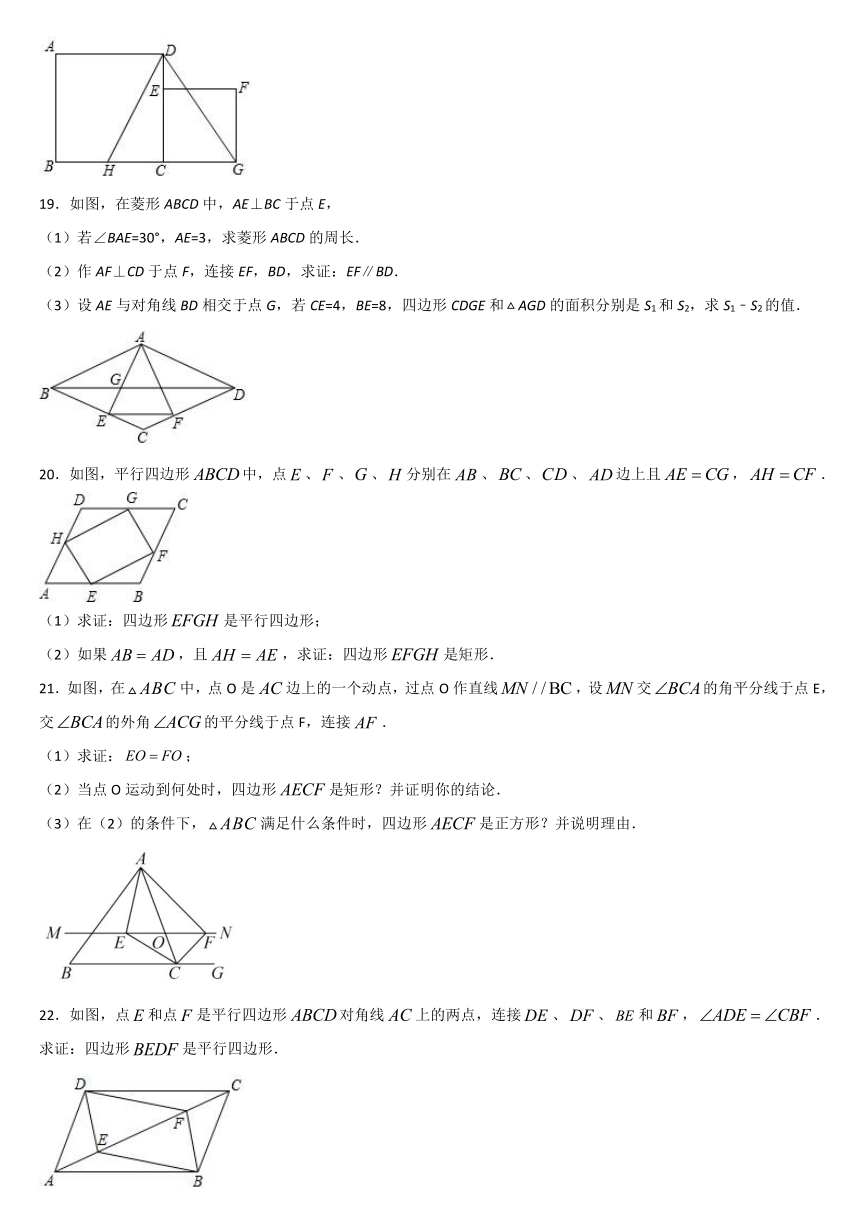
18.如图,已知正方形ABCD的边长为12,点E在DC边上,点G在BC的延长线上,设正方形CEFG的面积为false,以线段AD和DE为邻边的矩形的面积为false,且false=falsefalse.
(1)求线段DE的长.
(2)若H为BC边上一点,CH=5,连接DH,DG,判断△DHG的形状.
19.如图,在菱形ABCD中,AE⊥BC于点E,
(1)若∠BAE=30°,AE=3,求菱形ABCD的周长.
(2)作AF⊥CD于点F,连接EF,BD,求证:EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和falseAGD的面积分别是S1和S2,求S1﹣S2的值.
20.如图,平行四边形false中,点false、false、false、false分别在false、false、false、false边上且false,false.
(1)求证:四边形false是平行四边形;
(2)如果false,且false,求证:四边形false是矩形.
21.如图,在false中,点O是false边上的一个动点,过点O作直线false,设false交false的角平分线于点E,交false的外角false的平分线于点F,连接false.
(1)求证:false;
(2)当点O运动到何处时,四边形false是矩形?并证明你的结论.
(3)在(2)的条件下,false满足什么条件时,四边形false是正方形?并说明理由.
22.如图,点false和点false是平行四边形false对角线false上的两点,连接false、false、false和false,false.
求证:四边形false是平行四边形.
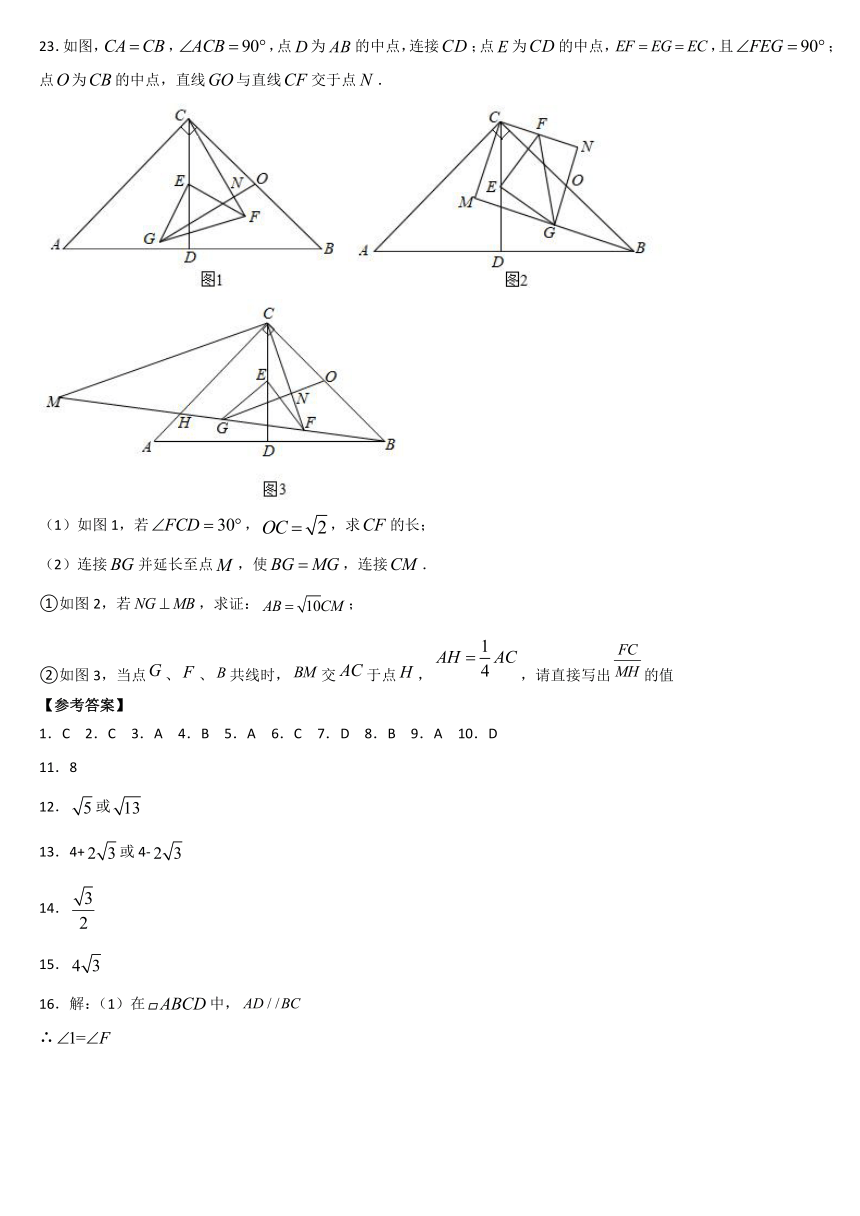
23.如图,false,false,点false为false的中点,连接false;点false为false的中点,false,且false;点false为false的中点,直线false与直线false交于点false.
(1)如图1,若false,false,求false的长;
(2)连接false并延长至点false,使false,连接false.
①如图2,若false,求证:false;
②如图3,当点false、false、false共线时,false交false于点false,false,请直接写出false的值
【参考答案】
1.C 2.C 3.A 4.B 5.A 6.C 7.D 8.B 9.A 10.D
11.8
12.false或false
13.4+false或4-false
14.false
15.false
16.解:(1)在false中,false
∴false
又∵false且false
∴false
∴false,
又false且false
∴false
∴false
∴false平分false;
(2)∵false
∴false
∴false,false
∵false
∴false
∴false
17.∵四边形false是平行四边形,
∴false.
∴false.
又∵false,false
∴false.
在△BEA与△CFB中
false
∴false(AAS)
∴false.
∴四边形false是菱形.
18.解:(1)设正方形CEFG的边长为a,
∵正方形ABCD的边长为12,
∴DE=12﹣a,
∵false=falsefalse,
∴false=false×12×(12﹣a),
解得:a=8,或a=﹣24,不符合题意,舍去,
∴DE=12﹣8=4;
(2)△DHG是等腰三角形;理由如下:
∵四边形ABCD和四边形CEFG是正方形,
∴∠DCH=∠DCG=90°,CD=12,CG=8,
∴DH=false=false=13,
DG=false=false=4false,
∵CH=5,
∴GH=CG+CH=13,
∴DH=GH,
∴△DHG是等腰三角形.
19.(1)解:∵AE⊥BC,∠BAE=30°,
∴false,false,
∵false,
∴false,
解得:false,
∴菱形false的周长=2false×4=8false;
(2)证明:∵四边形false是菱形,
∴∠false=∠false,false,
∵false,false,
∴∠false=∠false=90°,
在false和false中,false,
∴false(false),
∴false,
∵false,
∴false,
∴false,
∴false∥false;
(3)解:连接CG,如图所示:
∵四边形false是菱形,
∴false,false,
在false和false中,false,
∴false,
∴false,false和false的面积相等,
∴S1﹣S2=S△CGE,
false,
∵false,
∴falsefalse=4false,
设false,则false,
∵false,
∴false2+false2=false2,即:x2+42=(4false﹣x)2,
解得:x=false,即EG=false,
∴S1﹣S2=S△CGE=falseCE?EG=false×4×false=false.
20.解:(1)在平行四边形false中,false,
又∵false,false,
∴false.
∴false.
在平行四边形false中,false,false,
∴false,false,
即false,false.
又∵在平行四边形false中,false,
∴false.
∴false.
∴四边形false是平行四边形.
(2)在平行四边形false中,false,false.
设false,则false.
∵false,
∴false.
∵false,false,
∴false,即false.
∴false.
∴false.
又∵四边形false是平行四边形,
∴四边形false是矩形.
21.(1)证明:如图,∵false,
∴false.
又∵false平分false,∴false,
∴false,
∴false,
同理,false,
∴false.
(2)解:当点O运动到false的中点时,四边形false是矩形,
证明如下:当点O运动到false的中点时,false.
又∵false,
∴四边形false是平行四边形,
由(1)可知,false,
∴false,
∴false,即false,
∴四边形false是矩形.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
在(2)的条件下,false满足false为直角时,四边形false是正方形.
理由:由(2)知,当点O运动到false的中点时,四边形false是矩形.
∵false,
∴false,
当false时,false,即false,
∴四边形false是正方形.
22.解:证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
在△ADE和△CBF中,false,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠CFB,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形BEDF是平行四边形.
23.(1)解:如图1中,连接OE,过点E作EH⊥CF于H.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,∠ACD=∠BCD=45°,
∵CE=ED,CO=OB,
∴OE∥BD,
∴∠CEO=∠CDB=90°,
∴△CEO是等腰直角三角形,
∵OC=false,
∴EC=OE=1,
∵EC=EF,EH⊥CF,
∴CH=HF=EC?cos30°=false,
∴CF=2CH=false.
(2)①证明:连接OE.设CM=2a.
∵∠CEO=∠FEG=90°,
∴∠CEF=∠OEG,
∵EC=EF=EO=EG,
∴∠ECF=∠EFC=∠EOG=∠EGO,
∵∠EFC+∠EFN=180°,
∴∠EGO+∠EFN=180°,
∴∠N+∠FEG=180°,
∴∠N=90°,
∵NG⊥BM,
∴∠N=∠OGB=90°,
∵CO=OB,∠CON=∠BOG,
∴△CON≌△BOG(AAS),
∴CN=BG=MG,
∵CN∥BM,
∴四边形CMGN是平行四边形,
∵∠N=90°,
∴四边形CMGN是矩形,
∵∠ECF=∠EGO,∠ECO=∠EGF=45°,
∴∠NCO=∠FCN,
∵∠N=∠N,CO=CF,
∴△CNO≌△CNF(AAS),
∴CN=NG,
∴四边形CMGN是正方形,
∴CN=NG=2a,ON=OG=a,
∴CO=OB=falsea,
∴BC=2falsea,
∴AB=falseBC=2falsea,
∵CM=2a,
∴AB=falseCM.
②解:连接OE.设EF交OG于J.
∵∠CEO=∠FEG=90°,
∴∠CEF=∠OEG,
∵CE=OE=EF=EG,
∴△CEF≌△OEG(SAS),
∴CF=OG,∠EFC=∠EGO,
∵∠EGO+∠EJG=90°,∠GJE=∠FJN,
∴∠FJN+∠JFN=90°,
∴CF⊥OG,
∵OC=OB,GB=GM,
∴OG=falseCM,OG∥CM,
∴CM⊥CF,∠M=∠OGB,设CF=OG=a,则CM=2a,FM=falsea,
∵∠MCF=∠ACB,
∴∠MCA=∠BCF,
∵∠BCD=∠EGF=45°,∠ECF=∠EFC=∠EGO=∠EOG,
∴∠BCF=∠BGO,
∴∠HMC=∠HCM,
∴HM=HC,
∵∠M+∠CFM=90°,∠HCM+∠HCF=90°,
∴∠HCF=∠HFC,
∴HC=HF,
∴HM=FH=falsea,
∴false.
一、选择题
1.矩形ABCD中,AB=6,BC=8,则点A到BD的距离是( )
A.4 B.4.6 C.4.8 D.5
2.已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①④ B.①③④ C.②③ D.②③④
3.下列说法正确的是( )
①平行四边形的对角线互相平分;②菱形的四个内角相等;③矩形的对角线相等且互相垂直;④正方形具有矩形和菱形的所有性质.
A.①④ B.①③ C.②④ D.③④
4.下列命题中,正确的是( ).
A.两邻边相等的四边形是菱形 B.一条对角线平分一个内角的平行四边形是菱形
C.对角线垂直且一组邻边相等的四边形是菱形 D.对角线垂直的四边形是菱形
5.一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为( )
A.50或40或30 B.50或40 C.50 D.50或30或20
6.如图.在矩形ABCD中,对角线AC与BD交于点O,已知AO=5,∠AOB=60°,则下列选项中图形的周长是有理数的是( )
A.falseABC B.falseBOC C.falseCOD D.矩形ABCD
7.菱形false中,false.点false、false分别在边false、false上,且false.若false,则false的面积为( ).
A.false B.false C.false D.false
8.如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=40°,则∠E的度数是( )
A.10° B.20° C.30° D.40°
9.如图,正方形false和正方形false的顶点false在同一直线false上,且false,给出下列结论:
①false,
②false,
③false的面积false,
④false,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
10.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM//FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.若正方形false的对角线false的长为4,则该正方形的面积为_________.
12.已知,在△ABC中,∠BAC=45°,AB=1,AC=false,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为________.
13.已知false的周长为56,自顶点A作false于点E,false于点F,若false,false,则false_________________.
14.如图,将长,宽分别为false,1的长方形纸片剪成四个等腰三角形纸片(无余纸片).则四个等腰三角形的腰长均为_______.
15.如图,在false中,false,false,false,点P为false上任意一点,连接false,以false,false为邻边作平行四边形false,连接false,则false的最小值为______.
三、解答题
16.如图,在平行四边形false中,点E是CD边的中点,连接AE并延长交BC的延长线于点F,连接BE,false.
(1)求证:AE平分false;
(2)若false,false,求平行四边形false的面积.
17.如图,在false中,过点B作false,垂足为E,过点C作false,交false的延长线于点false.求证:四边形false是菱形.
18.如图,已知正方形ABCD的边长为12,点E在DC边上,点G在BC的延长线上,设正方形CEFG的面积为false,以线段AD和DE为邻边的矩形的面积为false,且false=falsefalse.
(1)求线段DE的长.
(2)若H为BC边上一点,CH=5,连接DH,DG,判断△DHG的形状.
19.如图,在菱形ABCD中,AE⊥BC于点E,
(1)若∠BAE=30°,AE=3,求菱形ABCD的周长.
(2)作AF⊥CD于点F,连接EF,BD,求证:EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和falseAGD的面积分别是S1和S2,求S1﹣S2的值.
20.如图,平行四边形false中,点false、false、false、false分别在false、false、false、false边上且false,false.
(1)求证:四边形false是平行四边形;
(2)如果false,且false,求证:四边形false是矩形.
21.如图,在false中,点O是false边上的一个动点,过点O作直线false,设false交false的角平分线于点E,交false的外角false的平分线于点F,连接false.
(1)求证:false;
(2)当点O运动到何处时,四边形false是矩形?并证明你的结论.
(3)在(2)的条件下,false满足什么条件时,四边形false是正方形?并说明理由.
22.如图,点false和点false是平行四边形false对角线false上的两点,连接false、false、false和false,false.
求证:四边形false是平行四边形.
23.如图,false,false,点false为false的中点,连接false;点false为false的中点,false,且false;点false为false的中点,直线false与直线false交于点false.
(1)如图1,若false,false,求false的长;
(2)连接false并延长至点false,使false,连接false.
①如图2,若false,求证:false;
②如图3,当点false、false、false共线时,false交false于点false,false,请直接写出false的值
【参考答案】
1.C 2.C 3.A 4.B 5.A 6.C 7.D 8.B 9.A 10.D
11.8
12.false或false
13.4+false或4-false
14.false
15.false
16.解:(1)在false中,false
∴false
又∵false且false
∴false
∴false,
又false且false
∴false
∴false
∴false平分false;
(2)∵false
∴false
∴false,false
∵false
∴false
∴false
17.∵四边形false是平行四边形,
∴false.
∴false.
又∵false,false
∴false.
在△BEA与△CFB中
false
∴false(AAS)
∴false.
∴四边形false是菱形.
18.解:(1)设正方形CEFG的边长为a,
∵正方形ABCD的边长为12,
∴DE=12﹣a,
∵false=falsefalse,
∴false=false×12×(12﹣a),
解得:a=8,或a=﹣24,不符合题意,舍去,
∴DE=12﹣8=4;
(2)△DHG是等腰三角形;理由如下:
∵四边形ABCD和四边形CEFG是正方形,
∴∠DCH=∠DCG=90°,CD=12,CG=8,
∴DH=false=false=13,
DG=false=false=4false,
∵CH=5,
∴GH=CG+CH=13,
∴DH=GH,
∴△DHG是等腰三角形.
19.(1)解:∵AE⊥BC,∠BAE=30°,
∴false,false,
∵false,
∴false,
解得:false,
∴菱形false的周长=2false×4=8false;
(2)证明:∵四边形false是菱形,
∴∠false=∠false,false,
∵false,false,
∴∠false=∠false=90°,
在false和false中,false,
∴false(false),
∴false,
∵false,
∴false,
∴false,
∴false∥false;
(3)解:连接CG,如图所示:
∵四边形false是菱形,
∴false,false,
在false和false中,false,
∴false,
∴false,false和false的面积相等,
∴S1﹣S2=S△CGE,
false,
∵false,
∴falsefalse=4false,
设false,则false,
∵false,
∴false2+false2=false2,即:x2+42=(4false﹣x)2,
解得:x=false,即EG=false,
∴S1﹣S2=S△CGE=falseCE?EG=false×4×false=false.
20.解:(1)在平行四边形false中,false,
又∵false,false,
∴false.
∴false.
在平行四边形false中,false,false,
∴false,false,
即false,false.
又∵在平行四边形false中,false,
∴false.
∴false.
∴四边形false是平行四边形.
(2)在平行四边形false中,false,false.
设false,则false.
∵false,
∴false.
∵false,false,
∴false,即false.
∴false.
∴false.
又∵四边形false是平行四边形,
∴四边形false是矩形.
21.(1)证明:如图,∵false,
∴false.
又∵false平分false,∴false,
∴false,
∴false,
同理,false,
∴false.
(2)解:当点O运动到false的中点时,四边形false是矩形,
证明如下:当点O运动到false的中点时,false.
又∵false,
∴四边形false是平行四边形,
由(1)可知,false,
∴false,
∴false,即false,
∴四边形false是矩形.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
在(2)的条件下,false满足false为直角时,四边形false是正方形.
理由:由(2)知,当点O运动到false的中点时,四边形false是矩形.
∵false,
∴false,
当false时,false,即false,
∴四边形false是正方形.
22.解:证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
在△ADE和△CBF中,false,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠CFB,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形BEDF是平行四边形.
23.(1)解:如图1中,连接OE,过点E作EH⊥CF于H.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,∠ACD=∠BCD=45°,
∵CE=ED,CO=OB,
∴OE∥BD,
∴∠CEO=∠CDB=90°,
∴△CEO是等腰直角三角形,
∵OC=false,
∴EC=OE=1,
∵EC=EF,EH⊥CF,
∴CH=HF=EC?cos30°=false,
∴CF=2CH=false.
(2)①证明:连接OE.设CM=2a.
∵∠CEO=∠FEG=90°,
∴∠CEF=∠OEG,
∵EC=EF=EO=EG,
∴∠ECF=∠EFC=∠EOG=∠EGO,
∵∠EFC+∠EFN=180°,
∴∠EGO+∠EFN=180°,
∴∠N+∠FEG=180°,
∴∠N=90°,
∵NG⊥BM,
∴∠N=∠OGB=90°,
∵CO=OB,∠CON=∠BOG,
∴△CON≌△BOG(AAS),
∴CN=BG=MG,
∵CN∥BM,
∴四边形CMGN是平行四边形,
∵∠N=90°,
∴四边形CMGN是矩形,
∵∠ECF=∠EGO,∠ECO=∠EGF=45°,
∴∠NCO=∠FCN,
∵∠N=∠N,CO=CF,
∴△CNO≌△CNF(AAS),
∴CN=NG,
∴四边形CMGN是正方形,
∴CN=NG=2a,ON=OG=a,
∴CO=OB=falsea,
∴BC=2falsea,
∴AB=falseBC=2falsea,
∵CM=2a,
∴AB=falseCM.
②解:连接OE.设EF交OG于J.
∵∠CEO=∠FEG=90°,
∴∠CEF=∠OEG,
∵CE=OE=EF=EG,
∴△CEF≌△OEG(SAS),
∴CF=OG,∠EFC=∠EGO,
∵∠EGO+∠EJG=90°,∠GJE=∠FJN,
∴∠FJN+∠JFN=90°,
∴CF⊥OG,
∵OC=OB,GB=GM,
∴OG=falseCM,OG∥CM,
∴CM⊥CF,∠M=∠OGB,设CF=OG=a,则CM=2a,FM=falsea,
∵∠MCF=∠ACB,
∴∠MCA=∠BCF,
∵∠BCD=∠EGF=45°,∠ECF=∠EFC=∠EGO=∠EOG,
∴∠BCF=∠BGO,
∴∠HMC=∠HCM,
∴HM=HC,
∵∠M+∠CFM=90°,∠HCM+∠HCF=90°,
∴∠HCF=∠HFC,
∴HC=HF,
∴HM=FH=falsea,
∴false.
