17.1.2 勾股定理的应用课件(28张)
文档属性
| 名称 | 17.1.2 勾股定理的应用课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 557.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 10:35:39 | ||
图片预览








文档简介
八年级下册
勾股定理的应用
学习目标
1、会从简单的实际问题中抽象出数学问题;
2、会用勾股定理解决简单的实际问题.
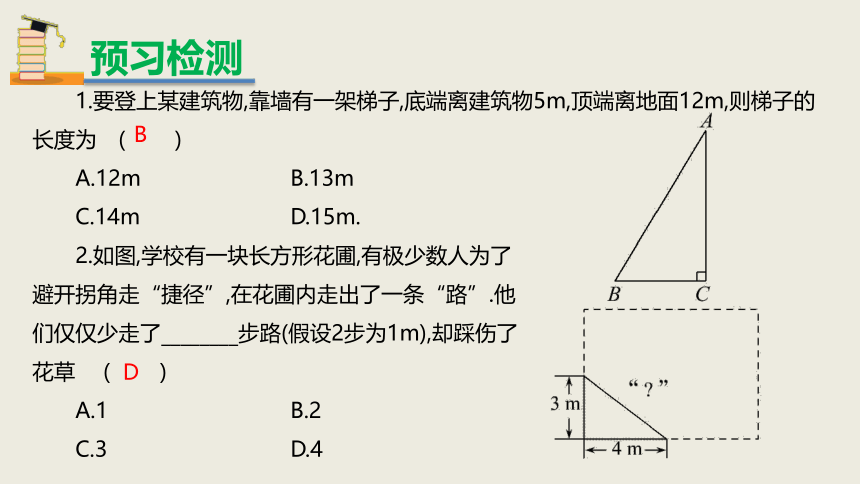
1.要登上某建筑物,靠墙有一架梯子,底端离建筑物5m,顶端离地面12m,则梯子的长度为 ( )
A.12m B.13m
C.14m D.15m.
2.如图,学校有一块长方形花圃,有极少数人为了
避开拐角走“捷径”,在花圃内走出了一条“路”.他
们仅仅少走了________步路(假设2步为1m),却踩伤了
花草 ( )
A.1 B.2
C.3 D.4
B
D
预习检测
3. 如图,一根长5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,那么竹竿底端B外移的距离BD ( )
A.等于1米 B.大于1米
C.小于1米 D.以上都不对
4.如图所示的长方体是某种饮料的纸质包装盒,规格为
5×6×10(单位:cm),在上盖中开有一孔便于插吸管,吸管长为
13cm,小孔到图中边AB距离为1cm,到上盖中与AB相邻的两
边距离相等,设插入吸管后露在盒外面的管长为hcm,则h的最
小值大约为_______cm.
(精确到个位,参考数据: ≈1.4, ≈1.7, ≈2.2).
A
2
课堂导入
如图所示,一棱长为3 cm的正方体.把所有的面都分成3×3个小正方形,假若一只蚂蚁每秒爬2 cm,则它从下底面A点,沿表面爬行至右侧的B点,最少要花几秒?
探究点一
问题1:一个门框尺寸如右图所示,一块长3m,宽2.2m的薄木板能否从门框内穿过?为什么?
解:在Rt△ABC中,
根勾股定理,得AC2=AB2+BC2=12+22=5
AC= ≈2.236
因为AC大于木板的宽,所以木板能从门框内通过.
课堂探究
问题2:如右图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
解:∵BD=OD-OB,∴求BD,可以先求OB,OD.
在Rt△AOB中,OB2=AB2-AO2=32-2.52=2.75,
∴OB= ≈1.658.
在Rt△COD中,OD2=AB2-OC2=32-22=5,
∴OD= ≈2.236.
∴BD=OD-OB≈2.236-1.658=0.578≈0.58.
因此,梯子的顶端沿墙下滑0.5m,梯子底端外移约0.58m.
生活中的一些实际问题常常通过构建数学模型(直
角三角形)来求解,勾股定理在生活中应用面广,建立
的模型有时并不是已知两边求第三边,而只是告诉了
其中的一些关系,一般可设未知数,用未知数表示它
们之间的关系,然后根据勾股定理列方程解决问题.
方法总结
例1.有一个边长为50dm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长(结果保留整数)?
解:如图,在Rt△ABC中,AB=BC=50dm.
AC2=AB2+BC2=502+502=500
∴AC= ≈71(dm)
因此,圆的直径至少为71dm长.
例题解析
例2如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m.你能求出A、B两点间的距离吗?(结果保留整数)
解:在Rt△ABC中,BC=60,AC=20.
AB2=BC2-AC2
=602-202
=3200
AB= ≈57
因此,A、B两点间的距离约为57m.
1、 (中考·安顺)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8米
B.10米
C.12米
D.14米
B
试一试
2、(中考·绍兴)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米 B.1.5米
C.2.2米 D.2.4米
C
3、(中考·黄冈)在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5 m,在地面的点E处,测得标语牌点A的仰角(即∠AEB)为30°,在地面的点F处,测得标语牌点A的仰角(即∠AFB)为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1 m,参考数据:2?≈1.41, 3?≈1.73)
?
解:如图,作FH⊥AE于H.
由题意可知∠HAF=∠HFA=45°,
∴AH=HF,
设AH=HF=x m,则EF=2x m,EH= 3?x m,
在Rt△AEB中,∵∠E=30°,AB=5 m,
∴AE=2AB=10 m,
∴x+ 3?x=10,∴x=5 3?-5,
∴EF=10 3?-10≈7.3(m),
答:点E与点F之间的距离约为7.3 m.
?
探究点二
问题:如图1所示,有一个圆柱,它的高等于
12 cm,底面上圆的周长等于18 cm.在圆柱
下底面的点A处有一只蚂蚁,它想吃到上底
面与点A相对的点B处的食物,沿圆柱侧面
爬行的最短路程是多少?
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面
画出几条路线,你觉得哪条路线最短呢?
图1
课堂探究
(2)如图2所示,将圆柱侧
面剪开展成一个长方形,从点
A到点B的最短路线是什么?你
画对了吗?
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱
侧面爬行的最短路程是多少?
(4)若蚂蚁先从点A直接爬到点C,然后再从点C沿地
面直径爬到点B,这样爬的总路程与沿圆柱侧面爬行的最
短路程比较,哪一条更短些?
图2
生活中的一些实际问题常常通过构建数学模型(直
角三角形)来求解,勾股定理在生活中应用面广,建立
的模型有时并不是已知两边求第三边,而只是告诉了
其中的一些关系,一般可设未知数,用未知数表示它
们之间的关系,然后根据勾股定理列方程解决问题.
方法总结
例3 如图所示的长方体的高为4 cm,底面是长为5 cm,宽为3 cm的长方形.一只蚂蚁从顶点A出发沿长方体的表面爬到顶点B.求:
(1)蚂蚁经过的最短路程;
(2)蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.
例题解析
解: (1)将长方体与顶点A,B相关的两个面展开,共有三种方式,
如图所示.若蚂蚁沿侧面爬行,如图①,则爬行的最短路程为
(5+3)2+42=80=45??(????????);
若蚂蚁沿侧面和上面爬行,如图②③,则爬行的最短路程分别为
(4+5)2+32=90=310?(????????),
(4+3)2+52=74?(????????).
因为74?<4 5?<3 10?,
所以蚂蚁经过的最短路程是74?cm.
(2)5+4+5+4+3+4+5=30(cm),所以蚂蚁沿着棱
爬行的最长路程是30 cm.
?
如图,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC=6 cm,P是母线BC上一点,且PC=23BC. 一只蚂蚁从点A出发沿着圆柱的侧面爬行到点P的最短距离是( )
A. 4+6?????cm B.5 cm
C.35? cm D.7 cm
?
B
试一试
1.如图,有两棵树,一棵高12m,另一棵高6m,
两树相距8m.一只鸟从一棵树的树梢飞到另一棵
树的树梢,问小鸟至少飞行________m.
2.有一只喜鹊在一棵3m高的小树上觅食,它的巢
筑在距离该树24m的一棵大树上,大树高14m,且巢离
树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果
它飞行的速度为5m/s,赶回巢中,它至少需要________s.
5.2
10
随堂检测
3.如图,是矗立在高速公路水平地面上的交通警示牌,
经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,
∠MBC=30°,则警示牌的高CD为________米(结果精确到
0.1米,参考数据: ≈1.41, ≈1.73).
4. 如图,有一长、宽、高分别为12cm,4cm,3cm的木
箱,在它里面放一根细木条(木条的粗细忽略不计),要求细木
条不能露出木箱,请你算一算,能放入的细木条的最大长度
是 ( )
A.13 cm B.14 cm
C.15 cm D.16 cm
2.9
A
5.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10 cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是 ( )
A.13 cm B.2 cm
C. cm D.2 cm
A
6.我国古代数学中有这样一道数学题:
有一棵枯树直立在地上,树高2丈,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,(如图)请问这根藤条有多长?
(注:枯树可以看成圆柱;树粗3尺,指的是:圆柱底面周长为3尺,1丈=10尺).
解:如图,在Rt△ABC中,
由勾股定理得AB2=BC2+AC2,
因为BC=20,AC=3×7=21,
所以AB2=202+212=841,
所以AB=29.所以这根藤条有29尺长.
7.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼梯铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼梯至少需要多少元钱?
解:地毯的长是楼梯的竖直部分与水平部分的和,即AC与BC的和,
在Rt△ABC中,由勾股定理得,AC2=AB2-BC2=132-52=144,
所以AC=12(m).
则地毯总长为12+5=17(m),
则地毯的总面积为17×2=34(m2),
所以铺完这个楼梯至少需要34×20=680(元).
利用勾股定理解决实际问题
课堂小结
书面作业:完成相关书本作业
布置作业
再见
勾股定理的应用
学习目标
1、会从简单的实际问题中抽象出数学问题;
2、会用勾股定理解决简单的实际问题.
1.要登上某建筑物,靠墙有一架梯子,底端离建筑物5m,顶端离地面12m,则梯子的长度为 ( )
A.12m B.13m
C.14m D.15m.
2.如图,学校有一块长方形花圃,有极少数人为了
避开拐角走“捷径”,在花圃内走出了一条“路”.他
们仅仅少走了________步路(假设2步为1m),却踩伤了
花草 ( )
A.1 B.2
C.3 D.4
B
D
预习检测
3. 如图,一根长5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,那么竹竿底端B外移的距离BD ( )
A.等于1米 B.大于1米
C.小于1米 D.以上都不对
4.如图所示的长方体是某种饮料的纸质包装盒,规格为
5×6×10(单位:cm),在上盖中开有一孔便于插吸管,吸管长为
13cm,小孔到图中边AB距离为1cm,到上盖中与AB相邻的两
边距离相等,设插入吸管后露在盒外面的管长为hcm,则h的最
小值大约为_______cm.
(精确到个位,参考数据: ≈1.4, ≈1.7, ≈2.2).
A
2
课堂导入
如图所示,一棱长为3 cm的正方体.把所有的面都分成3×3个小正方形,假若一只蚂蚁每秒爬2 cm,则它从下底面A点,沿表面爬行至右侧的B点,最少要花几秒?
探究点一
问题1:一个门框尺寸如右图所示,一块长3m,宽2.2m的薄木板能否从门框内穿过?为什么?
解:在Rt△ABC中,
根勾股定理,得AC2=AB2+BC2=12+22=5
AC= ≈2.236
因为AC大于木板的宽,所以木板能从门框内通过.
课堂探究
问题2:如右图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
解:∵BD=OD-OB,∴求BD,可以先求OB,OD.
在Rt△AOB中,OB2=AB2-AO2=32-2.52=2.75,
∴OB= ≈1.658.
在Rt△COD中,OD2=AB2-OC2=32-22=5,
∴OD= ≈2.236.
∴BD=OD-OB≈2.236-1.658=0.578≈0.58.
因此,梯子的顶端沿墙下滑0.5m,梯子底端外移约0.58m.
生活中的一些实际问题常常通过构建数学模型(直
角三角形)来求解,勾股定理在生活中应用面广,建立
的模型有时并不是已知两边求第三边,而只是告诉了
其中的一些关系,一般可设未知数,用未知数表示它
们之间的关系,然后根据勾股定理列方程解决问题.
方法总结
例1.有一个边长为50dm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长(结果保留整数)?
解:如图,在Rt△ABC中,AB=BC=50dm.
AC2=AB2+BC2=502+502=500
∴AC= ≈71(dm)
因此,圆的直径至少为71dm长.
例题解析
例2如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m.你能求出A、B两点间的距离吗?(结果保留整数)
解:在Rt△ABC中,BC=60,AC=20.
AB2=BC2-AC2
=602-202
=3200
AB= ≈57
因此,A、B两点间的距离约为57m.
1、 (中考·安顺)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8米
B.10米
C.12米
D.14米
B
试一试
2、(中考·绍兴)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米 B.1.5米
C.2.2米 D.2.4米
C
3、(中考·黄冈)在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5 m,在地面的点E处,测得标语牌点A的仰角(即∠AEB)为30°,在地面的点F处,测得标语牌点A的仰角(即∠AFB)为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1 m,参考数据:2?≈1.41, 3?≈1.73)
?
解:如图,作FH⊥AE于H.
由题意可知∠HAF=∠HFA=45°,
∴AH=HF,
设AH=HF=x m,则EF=2x m,EH= 3?x m,
在Rt△AEB中,∵∠E=30°,AB=5 m,
∴AE=2AB=10 m,
∴x+ 3?x=10,∴x=5 3?-5,
∴EF=10 3?-10≈7.3(m),
答:点E与点F之间的距离约为7.3 m.
?
探究点二
问题:如图1所示,有一个圆柱,它的高等于
12 cm,底面上圆的周长等于18 cm.在圆柱
下底面的点A处有一只蚂蚁,它想吃到上底
面与点A相对的点B处的食物,沿圆柱侧面
爬行的最短路程是多少?
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面
画出几条路线,你觉得哪条路线最短呢?
图1
课堂探究
(2)如图2所示,将圆柱侧
面剪开展成一个长方形,从点
A到点B的最短路线是什么?你
画对了吗?
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱
侧面爬行的最短路程是多少?
(4)若蚂蚁先从点A直接爬到点C,然后再从点C沿地
面直径爬到点B,这样爬的总路程与沿圆柱侧面爬行的最
短路程比较,哪一条更短些?
图2
生活中的一些实际问题常常通过构建数学模型(直
角三角形)来求解,勾股定理在生活中应用面广,建立
的模型有时并不是已知两边求第三边,而只是告诉了
其中的一些关系,一般可设未知数,用未知数表示它
们之间的关系,然后根据勾股定理列方程解决问题.
方法总结
例3 如图所示的长方体的高为4 cm,底面是长为5 cm,宽为3 cm的长方形.一只蚂蚁从顶点A出发沿长方体的表面爬到顶点B.求:
(1)蚂蚁经过的最短路程;
(2)蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.
例题解析
解: (1)将长方体与顶点A,B相关的两个面展开,共有三种方式,
如图所示.若蚂蚁沿侧面爬行,如图①,则爬行的最短路程为
(5+3)2+42=80=45??(????????);
若蚂蚁沿侧面和上面爬行,如图②③,则爬行的最短路程分别为
(4+5)2+32=90=310?(????????),
(4+3)2+52=74?(????????).
因为74?<4 5?<3 10?,
所以蚂蚁经过的最短路程是74?cm.
(2)5+4+5+4+3+4+5=30(cm),所以蚂蚁沿着棱
爬行的最长路程是30 cm.
?
如图,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC=6 cm,P是母线BC上一点,且PC=23BC. 一只蚂蚁从点A出发沿着圆柱的侧面爬行到点P的最短距离是( )
A. 4+6?????cm B.5 cm
C.35? cm D.7 cm
?
B
试一试
1.如图,有两棵树,一棵高12m,另一棵高6m,
两树相距8m.一只鸟从一棵树的树梢飞到另一棵
树的树梢,问小鸟至少飞行________m.
2.有一只喜鹊在一棵3m高的小树上觅食,它的巢
筑在距离该树24m的一棵大树上,大树高14m,且巢离
树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果
它飞行的速度为5m/s,赶回巢中,它至少需要________s.
5.2
10
随堂检测
3.如图,是矗立在高速公路水平地面上的交通警示牌,
经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,
∠MBC=30°,则警示牌的高CD为________米(结果精确到
0.1米,参考数据: ≈1.41, ≈1.73).
4. 如图,有一长、宽、高分别为12cm,4cm,3cm的木
箱,在它里面放一根细木条(木条的粗细忽略不计),要求细木
条不能露出木箱,请你算一算,能放入的细木条的最大长度
是 ( )
A.13 cm B.14 cm
C.15 cm D.16 cm
2.9
A
5.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10 cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是 ( )
A.13 cm B.2 cm
C. cm D.2 cm
A
6.我国古代数学中有这样一道数学题:
有一棵枯树直立在地上,树高2丈,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,(如图)请问这根藤条有多长?
(注:枯树可以看成圆柱;树粗3尺,指的是:圆柱底面周长为3尺,1丈=10尺).
解:如图,在Rt△ABC中,
由勾股定理得AB2=BC2+AC2,
因为BC=20,AC=3×7=21,
所以AB2=202+212=841,
所以AB=29.所以这根藤条有29尺长.
7.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼梯铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼梯至少需要多少元钱?
解:地毯的长是楼梯的竖直部分与水平部分的和,即AC与BC的和,
在Rt△ABC中,由勾股定理得,AC2=AB2-BC2=132-52=144,
所以AC=12(m).
则地毯总长为12+5=17(m),
则地毯的总面积为17×2=34(m2),
所以铺完这个楼梯至少需要34×20=680(元).
利用勾股定理解决实际问题
课堂小结
书面作业:完成相关书本作业
布置作业
再见
