6.3特殊平行四边形(3)课件 (19张)
文档属性
| 名称 | 6.3特殊平行四边形(3)课件 (19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 883.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
§6.3特殊的平行四边形(3)
菱形的性质与判定
学习目标
1.掌握菱形的定义以及菱形和平行四
边形的联系与区别.
2.掌握菱形的性质与判定,并能应用
它们进行有关的论证和计算.
一.复习回顾
1.平行四边形的定义及性质.
2.矩形的定义及性质.
3.动手操作
用一张纸剪一个平行四边形纸片,小组内的
同学互相比较一下所剪的平行四边形纸片,
看它们的形状有什么异同?
二.新知探究
探究一
菱形的定义
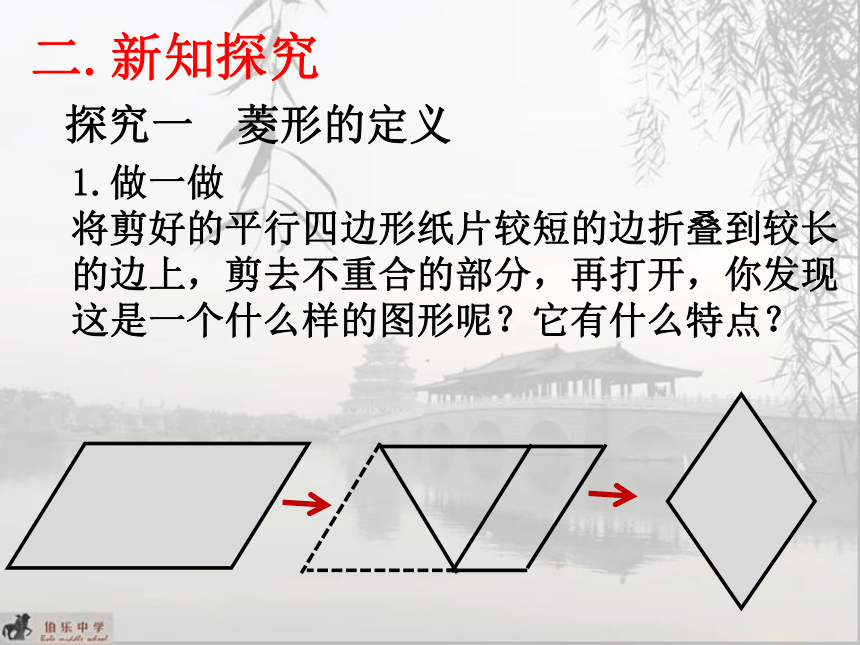
1.做一做
将剪好的平行四边形纸片较短的边折叠到较长
的边上,剪去不重合的部分,再打开,你发现
这是一个什么样的图形呢?它有什么特点?
2.结论:
这是个___图形,它的四条边_____,
是_______图形.
3.思考:它是我们前面学过的矩形吗?
4.概念
有一组邻边相等的平行四边形叫做菱形.
说明:菱形的定义既是菱形的性质,又是
作为判定一个四边形是否为菱形的依据.
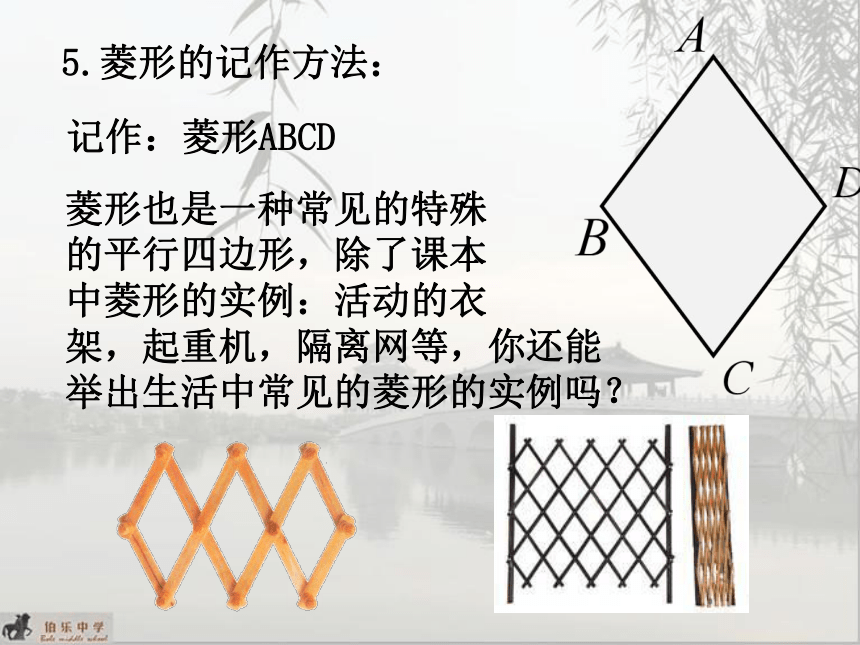
5.菱形的记作方法:
记作:菱形ABCD
菱形也是一种常见的特殊
的平行四边形,除了课本
中菱形的实例:活动的衣
架,起重机,隔离网等,你还能
举出生活中常见的菱形的实例吗?
探究二.菱形的性质
1.思考:菱形是特殊的平行四边形,它除了具有
平行四边形的所有的性质外,还具有哪些性质?
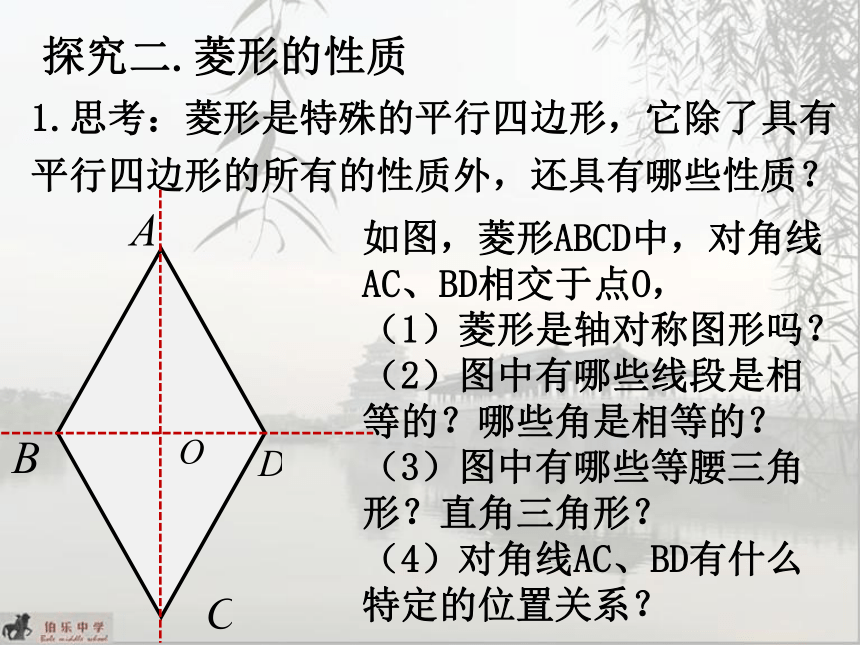
如图,菱形ABCD中,对角线
AC、BD相交于点O,
(1)菱形是轴对称图形吗?
(2)图中有哪些线段是相
等的?哪些角是相等的?
(3)图中有哪些等腰三角
形?直角三角形?
(4)对角线AC、BD有什么
特定的位置关系?
猜想得出命题:
1.四条边相等.
2.对角线互相垂直.
已知:在菱形ABCD中,AB=AD,对角线AC与BD
相交于点O,
求证:(1)AB=BC=CD=AD;
(2)AC⊥BD.
2.归纳:
(1)对称性:菱形是____图形.对称轴有____条
分别是______.
(2)边:菱形的四条边_____.
(3)对角线:菱形的对角线_____.
菱形的性质定理1
菱形的四条边都相等.
菱形的性质定理2
菱形的对角线互相垂直.
3.应用举例
例.如图,在菱形ABCD中,∠BAD=2∠B,试求
出∠B的度数,并说明△ABC是等边三角形.
解:在菱形ABCD中,
∠B+∠BAD=180°
又∵∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,AB=BC,
∴在△ABC中,∠BAC=∠BCA.
又∵∠B+∠BAC+∠BCA=180°,∠B=60°.
∴∠B=∠BAC=∠BCA=60°.
∴AB=BC=AC,即△ABC是等边三角形.
随堂练习
1.在菱形ABCD中,AB=3,∠ABC=60°,则对
角线AC=_____.
2.在菱形ABCD中,已知∠BAD=120°,AE⊥BC
垂足为点E.
求证:E是BC的中点.
探究三.菱形的判定
1.我们学习了菱形的性质,那么怎样判定一个
四边形是菱形?利用菱形的性质定理的逆命题
能探索菱形的判定定理吗?
2.菱形性质定理1的逆命题是什么?
(由学生思考、交流并进行几何论证,
教师规范学生的证明过程.)
四条边都相等的四边形是菱形.
菱形的判定定理1
3.菱形的性质定理2
菱形的对角线互相垂直.
它的逆命题是什么?
(1)对角线互相垂直的四边形是菱形.
假命题
(2)对角线互相垂直的平行四边形是菱形.
(或者对角线互相垂直平分的四边形是
平行四边形)
已知:如图,在四边形ABCD中,AC⊥BD,AC、BD
相交于点O.
求证:平行四边形是菱形.
证明:∵四边形ABCD是平行四边形.
∴BO=DO.
∵AC⊥BD,
∴AC是线段BD的垂直平分线.
∴AB=AD.
∴平行四边形ABCD是菱形.
菱形的判定定理2
对角线互相垂直的平行四边形是菱形.
4.应用举例
例如图,已知矩形ABCD的对角线AC的垂直平分
线与边AD、BC分别交于点E、F,
求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱
形,由已知条件可知EF⊥AC
所以只需证四边形AFCE是平
行四边形,又EF垂直平分AC
因此要证四边形AFCE是平行
四边形,只需证OE=OF.
随堂练习
1.如图,在矩形ABCD中,点E、F、G、H分别
是四条边的中点.试问四边形EFGH是什么样的
图形?并说明理由.
2.如果已知菱形的两条对角线长分别为a和b,
你能求出菱形的面积吗?
三.课堂小结
通过本课的学习,你有哪些收获?
还有什么疑惑?
四.作业
再见
§6.3特殊的平行四边形(3)
菱形的性质与判定
学习目标
1.掌握菱形的定义以及菱形和平行四
边形的联系与区别.
2.掌握菱形的性质与判定,并能应用
它们进行有关的论证和计算.
一.复习回顾
1.平行四边形的定义及性质.
2.矩形的定义及性质.
3.动手操作
用一张纸剪一个平行四边形纸片,小组内的
同学互相比较一下所剪的平行四边形纸片,
看它们的形状有什么异同?
二.新知探究
探究一
菱形的定义
1.做一做
将剪好的平行四边形纸片较短的边折叠到较长
的边上,剪去不重合的部分,再打开,你发现
这是一个什么样的图形呢?它有什么特点?
2.结论:
这是个___图形,它的四条边_____,
是_______图形.
3.思考:它是我们前面学过的矩形吗?
4.概念
有一组邻边相等的平行四边形叫做菱形.
说明:菱形的定义既是菱形的性质,又是
作为判定一个四边形是否为菱形的依据.
5.菱形的记作方法:
记作:菱形ABCD
菱形也是一种常见的特殊
的平行四边形,除了课本
中菱形的实例:活动的衣
架,起重机,隔离网等,你还能
举出生活中常见的菱形的实例吗?
探究二.菱形的性质
1.思考:菱形是特殊的平行四边形,它除了具有
平行四边形的所有的性质外,还具有哪些性质?
如图,菱形ABCD中,对角线
AC、BD相交于点O,
(1)菱形是轴对称图形吗?
(2)图中有哪些线段是相
等的?哪些角是相等的?
(3)图中有哪些等腰三角
形?直角三角形?
(4)对角线AC、BD有什么
特定的位置关系?
猜想得出命题:
1.四条边相等.
2.对角线互相垂直.
已知:在菱形ABCD中,AB=AD,对角线AC与BD
相交于点O,
求证:(1)AB=BC=CD=AD;
(2)AC⊥BD.
2.归纳:
(1)对称性:菱形是____图形.对称轴有____条
分别是______.
(2)边:菱形的四条边_____.
(3)对角线:菱形的对角线_____.
菱形的性质定理1
菱形的四条边都相等.
菱形的性质定理2
菱形的对角线互相垂直.
3.应用举例
例.如图,在菱形ABCD中,∠BAD=2∠B,试求
出∠B的度数,并说明△ABC是等边三角形.
解:在菱形ABCD中,
∠B+∠BAD=180°
又∵∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,AB=BC,
∴在△ABC中,∠BAC=∠BCA.
又∵∠B+∠BAC+∠BCA=180°,∠B=60°.
∴∠B=∠BAC=∠BCA=60°.
∴AB=BC=AC,即△ABC是等边三角形.
随堂练习
1.在菱形ABCD中,AB=3,∠ABC=60°,则对
角线AC=_____.
2.在菱形ABCD中,已知∠BAD=120°,AE⊥BC
垂足为点E.
求证:E是BC的中点.
探究三.菱形的判定
1.我们学习了菱形的性质,那么怎样判定一个
四边形是菱形?利用菱形的性质定理的逆命题
能探索菱形的判定定理吗?
2.菱形性质定理1的逆命题是什么?
(由学生思考、交流并进行几何论证,
教师规范学生的证明过程.)
四条边都相等的四边形是菱形.
菱形的判定定理1
3.菱形的性质定理2
菱形的对角线互相垂直.
它的逆命题是什么?
(1)对角线互相垂直的四边形是菱形.
假命题
(2)对角线互相垂直的平行四边形是菱形.
(或者对角线互相垂直平分的四边形是
平行四边形)
已知:如图,在四边形ABCD中,AC⊥BD,AC、BD
相交于点O.
求证:平行四边形是菱形.
证明:∵四边形ABCD是平行四边形.
∴BO=DO.
∵AC⊥BD,
∴AC是线段BD的垂直平分线.
∴AB=AD.
∴平行四边形ABCD是菱形.
菱形的判定定理2
对角线互相垂直的平行四边形是菱形.
4.应用举例
例如图,已知矩形ABCD的对角线AC的垂直平分
线与边AD、BC分别交于点E、F,
求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱
形,由已知条件可知EF⊥AC
所以只需证四边形AFCE是平
行四边形,又EF垂直平分AC
因此要证四边形AFCE是平行
四边形,只需证OE=OF.
随堂练习
1.如图,在矩形ABCD中,点E、F、G、H分别
是四条边的中点.试问四边形EFGH是什么样的
图形?并说明理由.
2.如果已知菱形的两条对角线长分别为a和b,
你能求出菱形的面积吗?
三.课堂小结
通过本课的学习,你有哪些收获?
还有什么疑惑?
四.作业
再见
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
