9.1.2不等式的性质 课件（29张）

(共27张PPT)
第九章
不等式与不等式组
学练优七年级数学下（RJ）
教学课件
9.1.2
不等式的性质
第1课时
不等式的性质
人教版七年级下册数学
1.理解并掌握不等式的基本性质;
2.通过实例操作,培养学生观察、分析、比较的能力,
会用不等式的基本性质解简单的不等式(重点、难
点)
学习目标
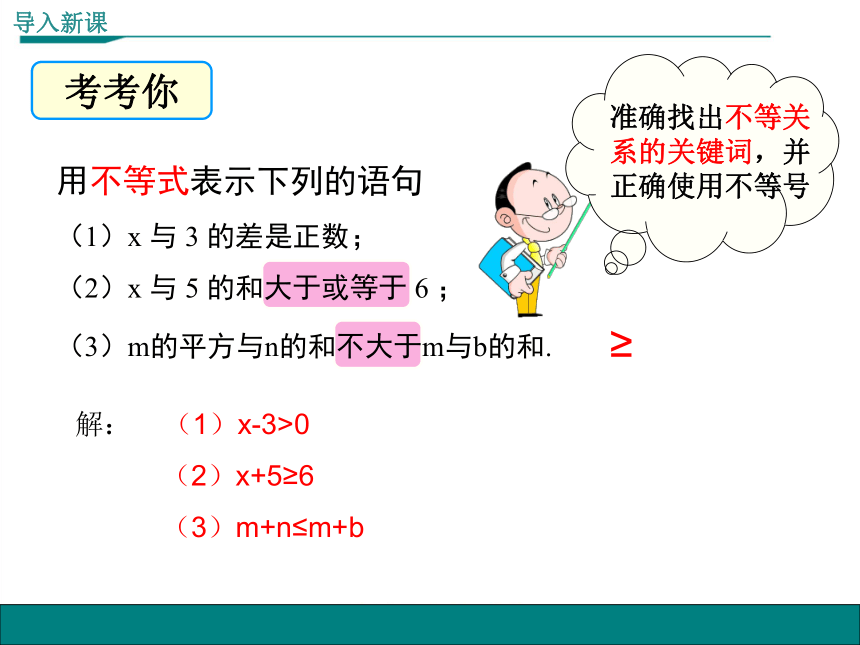
用不等式表示下列的语句
（1）x
与
3
的差是正数；
（2）x
与
5
的和大于或等于
6
；
（3）m的平方与n的和不大于m与b的和.
导入新课
考考你
准确找出不等关系的关键词，并正确使用不等号
解：
（1）x-3>0
（2）x+5≥6
（3）m+n≤m+b
≥
＞
＜
≥
≤
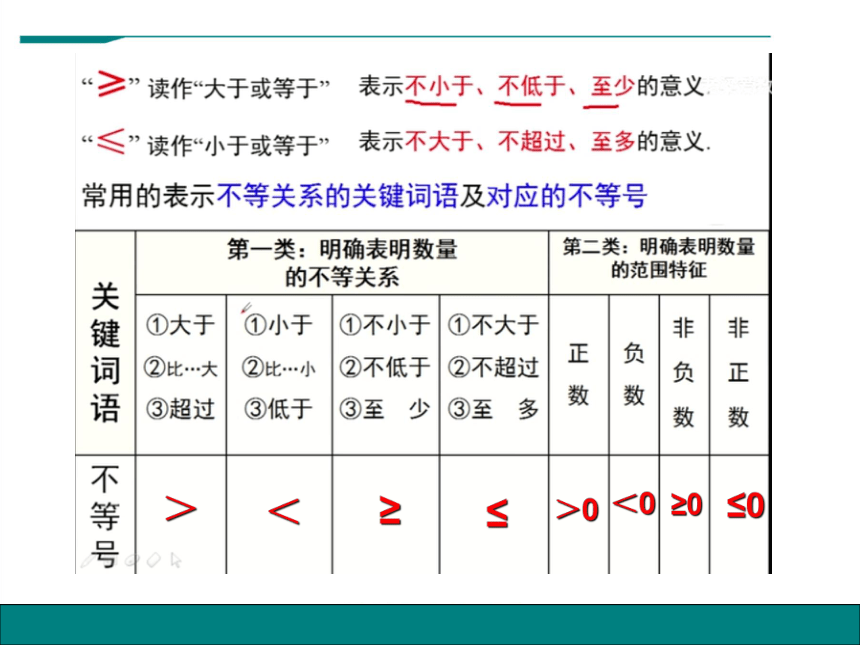
＞0
＜0
≥0
≤0
讲授新课
练一练
用不等号表示下列语句并直接说出解集.
（1）a
与
1
的差是非数；
（2）x
的3倍不大于
6
；
（3）4y不小于y的
2
倍与
3
的差
解：
（1）a-1≥0
（2）3x≤6
（3）4y≥2y-3
a≥1
x≤2
？
不等式是否也有类似的性质呢？
录自乐乐课堂
观看视频
1.探究不等式是否具有等式同样的性质；
2.如果有，那不等式具有什么性质？
规律探索
不等号的方向
　
6<10
不等式
７＞４
－3＜４
7+5
4+5
-3-7
4－7
不变
两边都加（或减去）同一个数
不等式
７＞
6+(a+b)
10+(a+b)
不变
不变
<
<
>
不等式基本性质1
不等式的两边都加上（或都减去）同一个数或（式），不等号的方向不变.
即，如果a>b，那么
a
+
c
>
b
+
c，且
a-c>b-c.
一般地，不等式具有如下性质：
一、不等式基本性质1
用不等号填空：
（1）5
3
；
5×2
3×2
；
5÷2
3÷2
.
（2）2
4
；
2×3
4×3
；
2÷4
4÷4
.
>
>
>
<
<
<
规律探索
不等式基本性质2
不等式的两边都乘（或除以）同一个正数，不等号的方向不变.
即，如果a
>
b，c
>
0，那么
ac
>
bc
，
>
.
一般地，不等式还有如下性质：
二、不等式基本性质2
用不等号填空：
（1）5
3
；
5×(－2)
3×2
；
5÷(-2)
3÷(-2)
.
（2）2
4
；
2×(－3)
4×(-3
)；
2÷(-4)
4÷(-4)
.
>
<
<
<
>
>
规律探索
不等式基本性质3
不等式的两边都乘（或除以）同一个负数，不等号的方向改变.
即，如果a
>
b，c
<
0，那么
ac
<
bc
，
<
.
三、不等式基本性质3
一般地，不等式还有如下性质：
（1）如果a＞b，那么ac＞bc.
（2）如果a＞b，那么ac2＞bc2.
（3）如果ac2＞bc2，那么a＞b.
你能用不等式的基本性质判断下列说法的正误吗？
×
×
√
因为c≠0，所以c2＞0.
当c≤0时，不成立.
当c=0时，不成立.
不等式的基本性质与等式的基本性质有什么相同点和不同点？
思考
比较等式与不等式的性质.
等式的基本性质1
　不等式的性质1
等式的基本性质2
　不等式的性质2
等式的两边都加上（或减去）同一个数，所得到的等式仍成立。
等式的两边都乘以（或除以）同一个不为零的数，所得的等式仍成立.
不等式的两边加（或减）同一个数（或式子），不等式的方向不变。
不等式的两边乘（或除以）同一个正数，不等号的方向不变。
不等式的性质3
不等式的两边乘（或除以）同一个负数，不等号的方向改变.
例1
利用不等式的性质解下列不等式：
(1)
x-7＞26；
(2)
3x<2x+1；
(3)
＞50；　　
(4)
-4x＞3.　　　　
解未知数为x的不等式
化为x＞a或x﹤a的形式
目标
方法：不等式基本性质1~3
利用不等式的性质解简单的不等式
二
思路：
解
(1)为了使不等式x-7＞26中不等号的一边变为x，
根据不等式的性质1，不等式两边都加7，不
等号的方向不变,得
x-7+7﹥26+7，即x﹥33.
这个不等式的解集在数轴上的表示如图所示：　
0
33
(2)为了使不等式3x<2x+1中不等号的一边变为x，根
据_____________，不等式两边都减去____，不等
号的方向_____，得
.
3x-2x﹤2x+1-2x
，即
x﹤1
这个不等式的解集在数轴上的表示如图所示：
0
1
不等式性质1
2x
不变
(3)为了使不等式
﹥50中不等号的一边变为x，根据
不等式的性质2，不等式的两边都除以　不等号的
方向不变，得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(4)为了使不等式-4x﹥3中的不等号的一边变为x，
根据______________，不等式两边都除以____，
不等号的方向______，得
x﹤-
.
这个不等式的解集在数轴上的表示如图所示：
－
4
3
0
不等式的性质3
-4
改变
下面是某同学根据不等式的性质做的一道题：
在不等式-4x+5>9的两边都减去5，得
-4x
>
4
在不等式-4x>
4的两边都除以-4，得
x
>
-1
请问他做对了吗？如果不对，请改正.
不对
x
<
-1
说一说
当堂练习
解：x
<
2
解：x
<
6
1.
把下列不等式化为x>a或x（1）5＞3+x；
（2）2x＜x+6.
2.利用不等式的性质解下列不等式,并再数轴上表示．
(2)-2x
>
3
(1)x-5
>
-1
(3)7x
<
6x-6
x＞4
x<-6
4
0
0
0
-6
例
某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位：cm3)表示新注入水的体积，写出V的取值范围.
例2
解：新注入水的体积V与原有水的体积的和不能超过
容器的容积，即
V+3×5×3≤3×5×10
解得
V≤105
又由于新注入水的体积不能是负数，因此，V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图
在表示0和105的点上画实心圆点，表示取值范围包括这两个数
0
105
课堂小结
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果
那么
应用
不等式的基本性质1
如果a>b，那么a+c>b+c，a-c>b-c
→
谢谢！