18.1.1 平行四边形的性质课件(23张)
文档属性
| 名称 | 18.1.1 平行四边形的性质课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 10:44:37 | ||
图片预览





文档简介
生活中的图形
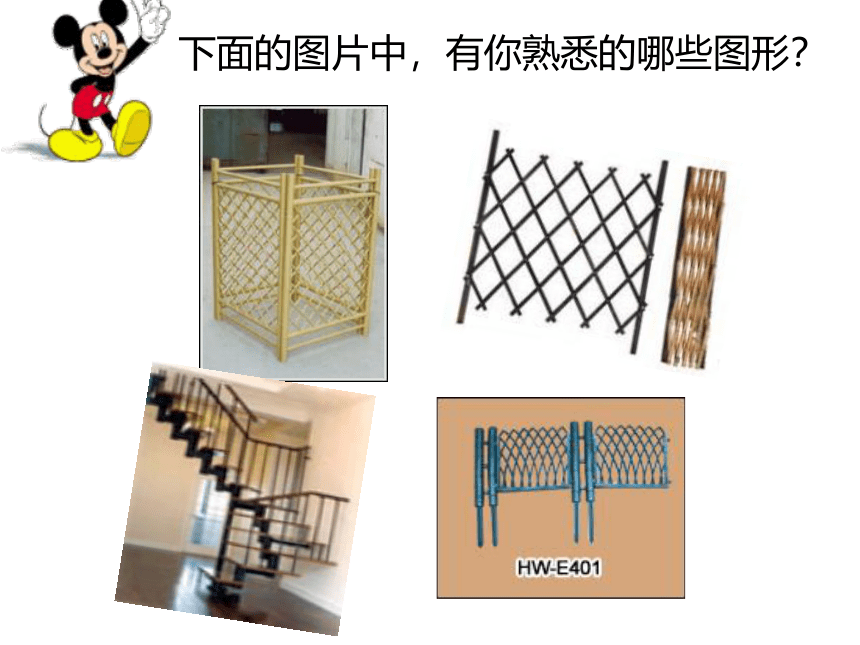
下面的图片中,有你熟悉的哪些图形?
平行四边形及其性质(一)
学习目标
1、在对平行四边形认识的基础上,探索并掌握平行四边形的性质。
2、会利用平行四边形的性质去解决实际问题。
平行四边形性质的认识和 掌握。
教学难点:
用简明的语言归纳平行四边形的性质。
教学重点:
A
B
C
D
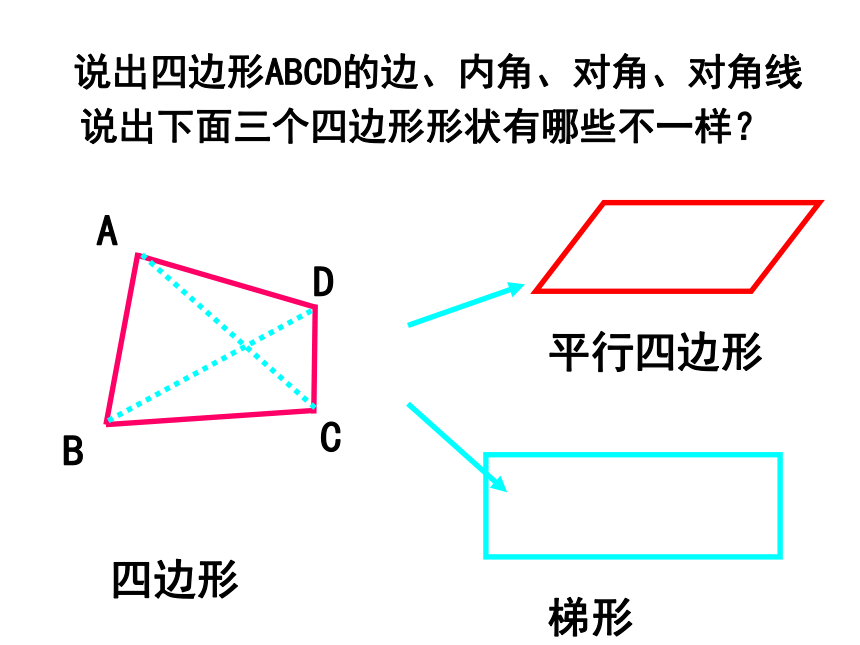
说出四边形ABCD的边、内角、对角、对角线
四边形
平行四边形
梯形
说出下面三个四边形形状有哪些不一样?
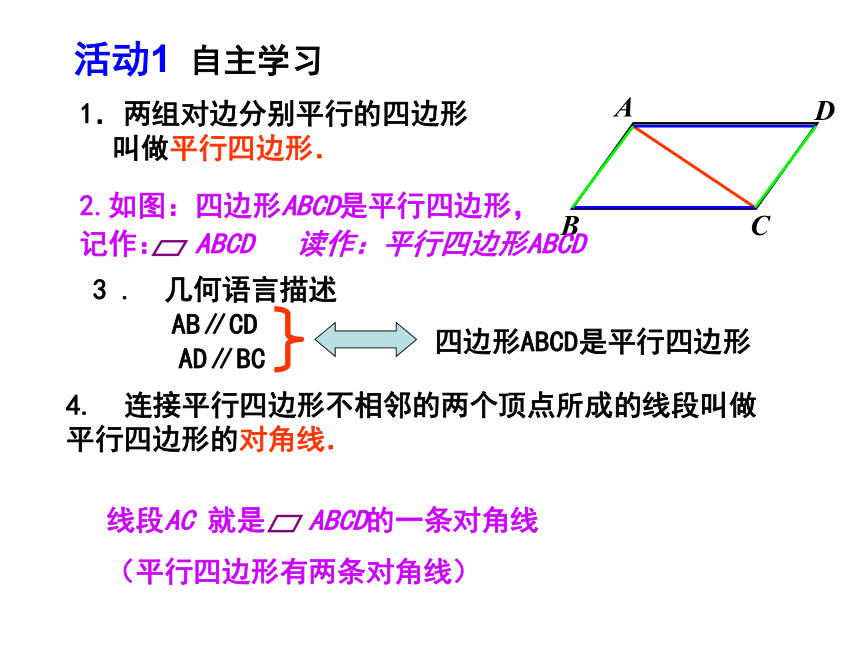
1.两组对边分别平行的四边形叫做平行四边形.
4. 连接平行四边形不相邻的两个顶点所成的线段叫做平行四边形的对角线.
活动1 自主学习
A
D
C
B
线段AC 就是 ABCD的一条对角线
(平行四边形有两条对角线)
2.如图:四边形ABCD是平行四边形,
记作: ABCD 读作:平行四边形ABCD
3 . 几何语言描述 AB∥CD
AD∥BC
四边形ABCD是平行四边形
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?
活动 2
A
B
C
D
探索交流------平行四边形的边有什么关系?
猜想:
平行四边形的对边平行且相等。
C
B
A
D
性质1:平行四边形的对边相等。
A
B
C
D
∵四边形ABCD是平行四边形
∴AB=CD,BC=AD
几何语言:
探索交流---
平行四边形的对角有什么关系?
猜想:平行四边形的对角相等。
思考:
平行四边形中相邻的两角有什么关系呢?
A
B
C
D
O
性质2:平行四边形的对角相等
A
B
C
D
∵四边形ABCD是平行四边形
∴ ∠ A= ∠ C, ∠ B= ∠ D
几何语言:
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的性质
总结归纳:
A
C
D
B
推理证明
∴AD∥BC ,AB∥CD
A
B
C
D
2
3
1
4
(平行四边形定义)
解:连接BD
∴∠1=∠2, ∠3=∠4
∵BD=DB
∴△ABD≌△CDB(ASA)
∴∠A=∠C AD=CB,AB=CD
∵∠1=∠2, ∠3=∠4
∴∠1+∠4=∠2+∠3(等式性质)
即∠ABC=∠ADC
∴ AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC
∵四边形ABCD是平行四边形
例题教学: ?
例: 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边的长各是多少?
解: ∵四边形ABCD是平行四边形
∵ AB=8
有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
活动 3
课堂回顾
1、定义:两组对边分别平行的四边形 叫做平行四边形。
2、性质:平行四边形的对边平行且相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3、性质的运用
A
D
B
C
40
(1)在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
30
120°
120°
60°
(2)在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
120°
40°
随堂练习? :
(3).下列性质中,平行四边形不一定具备
的是( )
(A)对角相等 (B)邻角互补
(C)对角互补 (D)内角和是360°
(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;
(4).下面判定四边形是平行四边形的方法中,
错误的是( )。
(C)一组对边平行,一组对角相等;
(D)一组对边平行,另一组对边相等
C
D
(5) 如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:∠BAE=∠DCF。
A
B
C
D
E
F
<一>看课本P82~P83
<二>课本P83~P84习题4.1(1,2,3)
<三>预习内容P84~P85
预习提纲:
(1)平行四边形的性质还有什么?
(2)两平行线间的距离的定义.
作业
下面的图片中,有你熟悉的哪些图形?
平行四边形及其性质(一)
学习目标
1、在对平行四边形认识的基础上,探索并掌握平行四边形的性质。
2、会利用平行四边形的性质去解决实际问题。
平行四边形性质的认识和 掌握。
教学难点:
用简明的语言归纳平行四边形的性质。
教学重点:
A
B
C
D
说出四边形ABCD的边、内角、对角、对角线
四边形
平行四边形
梯形
说出下面三个四边形形状有哪些不一样?
1.两组对边分别平行的四边形叫做平行四边形.
4. 连接平行四边形不相邻的两个顶点所成的线段叫做平行四边形的对角线.
活动1 自主学习
A
D
C
B
线段AC 就是 ABCD的一条对角线
(平行四边形有两条对角线)
2.如图:四边形ABCD是平行四边形,
记作: ABCD 读作:平行四边形ABCD
3 . 几何语言描述 AB∥CD
AD∥BC
四边形ABCD是平行四边形
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?
活动 2
A
B
C
D
探索交流------平行四边形的边有什么关系?
猜想:
平行四边形的对边平行且相等。
C
B
A
D
性质1:平行四边形的对边相等。
A
B
C
D
∵四边形ABCD是平行四边形
∴AB=CD,BC=AD
几何语言:
探索交流---
平行四边形的对角有什么关系?
猜想:平行四边形的对角相等。
思考:
平行四边形中相邻的两角有什么关系呢?
A
B
C
D
O
性质2:平行四边形的对角相等
A
B
C
D
∵四边形ABCD是平行四边形
∴ ∠ A= ∠ C, ∠ B= ∠ D
几何语言:
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的性质
总结归纳:
A
C
D
B
推理证明
∴AD∥BC ,AB∥CD
A
B
C
D
2
3
1
4
(平行四边形定义)
解:连接BD
∴∠1=∠2, ∠3=∠4
∵BD=DB
∴△ABD≌△CDB(ASA)
∴∠A=∠C AD=CB,AB=CD
∵∠1=∠2, ∠3=∠4
∴∠1+∠4=∠2+∠3(等式性质)
即∠ABC=∠ADC
∴ AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC
∵四边形ABCD是平行四边形
例题教学: ?
例: 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边的长各是多少?
解: ∵四边形ABCD是平行四边形
∵ AB=8
有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
活动 3
课堂回顾
1、定义:两组对边分别平行的四边形 叫做平行四边形。
2、性质:平行四边形的对边平行且相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3、性质的运用
A
D
B
C
40
(1)在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
30
120°
120°
60°
(2)在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
120°
40°
随堂练习? :
(3).下列性质中,平行四边形不一定具备
的是( )
(A)对角相等 (B)邻角互补
(C)对角互补 (D)内角和是360°
(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;
(4).下面判定四边形是平行四边形的方法中,
错误的是( )。
(C)一组对边平行,一组对角相等;
(D)一组对边平行,另一组对边相等
C
D
(5) 如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:∠BAE=∠DCF。
A
B
C
D
E
F
<一>看课本P82~P83
<二>课本P83~P84习题4.1(1,2,3)
<三>预习内容P84~P85
预习提纲:
(1)平行四边形的性质还有什么?
(2)两平行线间的距离的定义.
作业
